A Possible Failure of Determinism in General Relativity

Harvey Reall

Viewpoint

A Possible Failure of Determinism in General Relativity

Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom

January 17, 2018• Physics 11, 6

A numerical analysis of perturbations of a charged black hole suggests that the usual predictability of the laws of physics can fail in general relativity.

Figure caption — **Figure 1:** Gravitational collapse of a charged spherical star to form a charged black hole. Only the radial and time dimensions of spacetime are plotted. Light rays traveling radially away from, or towards, the star are straight lines at 45° to the horizontal. “Infinity” represents points infinitely far away from the star in space and/or time. The black hole is the region inside the event horizon. Initial data describing the star before collapse are specified on the surface shown. The region of spacetime that can be predicted from the initial data is bounded by the Cauchy horizon. The region of spacetime denoted with the question mark cannot be predicted from the initial data. The diagram also shows the trajectory of an observer who crosses the Cauchy horizon. The strong cosmic censorship conjecture asserts that Cauchy horizons are always unstable but Cardoso and colleagues’ work [1] suggests that this may not be true if the cosmological constant is positive.

Is the future predictable? If we know the initial state of a system exactly, then do the laws of physics determine its state arbitrarily far into the future? In Newtonian mechanics, the answer is yes. Similarly in electromagnetism: if one knows the initial state of the electric and magnetic fields exactly, then Maxwell’s equations determine their state at any later time. In quantum mechanics, if the initial wave function is known exactly, then Schrödinger’s equation can be used to predict the wave function at any later time. However, new research by Vitor Cardoso from the University of Lisbon, Portugal, and colleagues [1] suggests that this predictability of the laws of physics can fail in general relativity. The researchers find that it might be possible for a star that undergoes gravitational collapse to form a black hole containing a region in which physics cannot be predicted from the initial state of the star.

General relativity asserts that spacetime is dynamical, with its dynamics dictated by Einstein’s equation. Just as the initial state of a particle is specified by its position and velocity, an initial state for spacetime is specified by the geometry of space at some instant of time, as well as by its rate of change. Given such initial data, a fundamental theorem in general relativity [2] states that there is a so-called maximal Cauchy development. This is the largest spacetime that is uniquely determined by the initial data. But is it all of spacetime? In other words, could the maximal Cauchy development be a subset of a larger spacetime? By definition of the maximal Cauchy development, this larger spacetime could not be predicted from the initial data. This scenario would represent a failure of determinism: one would not be able to use the initial data to predict the state of spacetime arbitrarily far into the future.

Roger Penrose’s strong cosmic censorship conjecture [3] asserts that this scenario does not happen. It states that the maximal Cauchy development of generic initial data is never part of a larger spacetime. (Penrose also formulated a “weak” cosmic censorship conjecture, which states that when gravitational collapse of a star causes a spacetime singularity to form, this singularity is always hidden inside a black hole. Despite the names, the two conjectures are logically independent.)

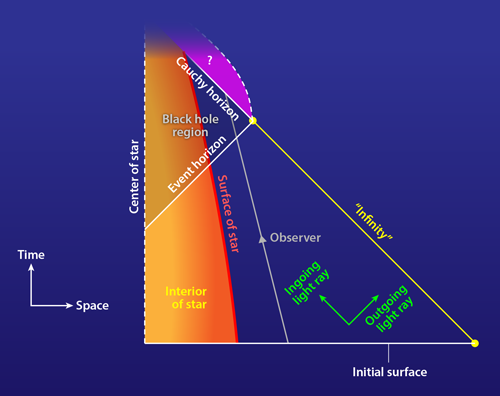
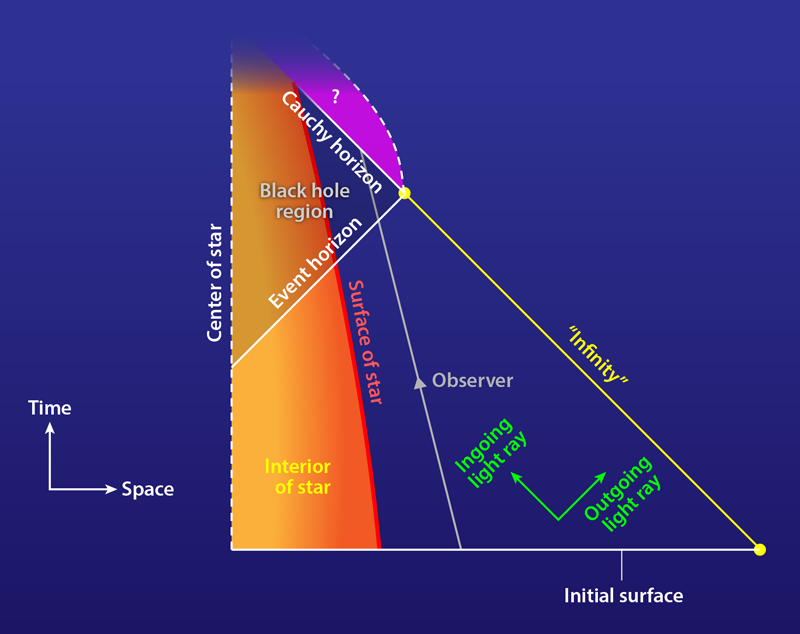
Electrically charged black holes appear to offer a counterexample to the strong cosmic censorship conjecture. Such a black hole results from the gravitational collapse of a charged spherical star (see Fig. 1). Consider the initial data describing the star before collapse. What is the maximal Cauchy development of this initial data? The black hole is described by a solution of Einstein’s equation known as the Reissner-Nordström solution. In a Reissner-Nordström black hole, the maximal Cauchy development is not the entire spacetime, but has a boundary—called the Cauchy horizon—inside the black hole. Spacetime remains smooth up to the Cauchy horizon, and it can be smoothly extended beyond the Cauchy horizon in infinitely many different ways, all satisfying Einstein’s equation. Therefore the maximal Cauchy development is part of a larger spacetime, in apparent contradiction with strong cosmic censorship.

However, this example is not really a violation of strong cosmic censorship because the Cauchy horizon is unstable. If one perturbs the initial data slightly, breaking the star’s spherical symmetry, then, generically, the resulting perturbed spacetime does not exhibit a Cauchy horizon but instead ends at a singularity (infinite spacetime curvature) where the Cauchy horizon used to be [4–6]. This instability is the reason for the word “generic” in the statement of the conjecture, which excludes only Cauchy horizons of the stable variety.

Great! Strong cosmic censorship is respected, the future is predictable. Well, maybe not. Einstein's equation includes the cosmological constant ( $Λ$ ), which explains the observed accelerating expansion of our Universe. Observations indicate that $Λ$ is very small, but nonzero, and positive. The smallness of $Λ$ usually implies that it can be ignored in studies of black holes. However, the strength of the Cauchy horizon instability depends on how quickly the perturbations discussed above decay outside the black hole: faster decay outside the hole leads to a weaker instability of the Cauchy horizon. With positive $Λ$ , perturbations outside the hole decay faster (exponentially) than with vanishing $Λ$ . Hence the Cauchy horizon instability is weaker when $Λ$ is positive [7].

For linear perturbations, the rate of decay can be obtained by looking at so-called quasinormal modes: damped oscillations of the black hole. Recent work [8] has proved that the strength of the Cauchy horizon instability is determined by the half-life of the most slowly decaying quasinormal modes. In their study, Cardoso and colleagues use numerical methods to determine the quasinormal modes of Reissner-Nordström black holes with positive $Λ$ . In particular, they identify the slowest decaying modes for many different values of the mass and charge of the hole. They argue that, when combined with results of a recent nonlinear study of the Cauchy horizon instability with positive $Λ$ [9], their results suggest the following picture. The curvature of the perturbed spacetime diverges at the Cauchy horizon. For most Reissner-Nordström black holes, this implies that strong cosmic censorship is respected. However, if the black hole charge is very close to the maximum possible value, then the divergence in curvature is sufficiently mild that the Einstein equation still makes sense at the Cauchy horizon. The perturbed spacetime can be extended beyond the Cauchy horizon, in infinitely many different ways, as a “weak” solution of the Einstein equation, in violation of strong cosmic censorship. In such cases, the divergence in curvature at the Cauchy horizon is similar to a shock in a fluid. It appears that this singularity is so weak that sufficiently robust physical bodies could cross the Cauchy horizon without being destroyed. Thus one could imagine an observer jumping into the black hole and crossing the Cauchy horizon. In this scenario, the observer’s fate cannot be predicted.

A proof that this picture is correct will require a better understanding of nonlinear effects. Such an understanding seems within reach: there are theorems relating decay of gravitational perturbations outside the black hole to (nonlinear) behavior at the Cauchy horizon [6, 9], and there has been recent progress in understanding nonlinear perturbations of black holes with positive $Λ$ [10].

Charged black holes are not relevant in astrophysics because large imbalances of charge do not occur in nature. However, uncharged rotating black holes also exhibit an unstable Cauchy horizon. Studying such black holes is harder than studying Reissner-Nordström black holes because rotating black holes possess fewer rotational symmetries than Reissner-Nordström black holes. It will be interesting to see what happens for uncharged rotating black holes with positive $Λ$ . The analogy with charged black holes suggests that holes rotating at almost the maximum possible rate may violate strong cosmic censorship.

Finally, our discussion has been based on classical general relativity, but the divergence in curvature may lead to large quantum effects near the Cauchy horizon. Whether these effects could strengthen the Cauchy horizon instability and thereby rescue determinism remains to be investigated.

This research is published in Physical Review Letters.

References

V. Cardoso, J. L. Costa, K. Destounis, P. Hintz, and A. Jansen, “Quasinormal Modes and Strong Cosmic Censorship,” Phys. Rev. Lett. 120, 031103 (2018).
Y. Choquet-Bruhat and R. P. Geroch, “Global Aspects of the Cauchy Problem in General Relativity,” Commun. Math. Phys. 14, 329 (1969).
R. Penrose, “Singularities of Spacetime,” in Theoretical Principles in Astrophysics and Relativity, edited by N. R. Liebowitz, W. H. Reid, and P. O. Vandervoort (Chicago University Press, Chicago, 1978), p. 217[Amazon][WorldCat].
M. Simpson and R. Penrose, “Internal Instability in a Reissner-Nordström Black Hole,” Int. J. Theor. Phys. 7, 183 (1973).
E. Poisson and W. Israel, “Internal Structure of Black Holes,” Phys. Rev. D 41, 1796 (1990).
M. Dafermos, “The Interior of Charged Black Holes and the Problem of Uniqueness in General Relativity,” Commun. Pure Appl. Math. 58, 0445 (2005).
F. Mellor and I. Moss, “Stability of Black Holes in De Sitter Space,” Phys. Rev. D 41, 403 (1990).
P. Hintz and A. Vasy, “Analysis of Linear Waves near the Cauchy Horizon of Cosmological Black Holes,” J. Math. Phys. 58, 081509 (2017).
J. L. Costa, P. M. Girão, J. Natário, and J. D. Silva, “On the Occurrence of Mass Inflation for the Einstein-Maxwell-Scalar Field System with a Cosmological Constant and an Exponential Price Law,” arXiv:1707.08975.
P. Hintz and A. Vasy, “The Global Non-Linear Stability of the Kerr-de Sitter Family of Black Holes,” arXiv:1606.04014.

About the Author

Harvey Reall is a Professor of Theoretical Physics at Cambridge University. He obtained his Ph.D. from Cambridge University in 2000 and subsequently held postdoctoral positions at Queen Mary University of London and at the University of California at Santa Barbara. He became a Lecturer at the University of Nottingham in 2005 and joined the faculty at Cambridge University in 2007.