A New Angle on Mapping the Refractive Index

Kareem Elsayad

Viewpoint

A New Angle on Mapping the Refractive Index

Vienna Biocenter, Dr.-Bohr-Gasse 3, 1030 Vienna, Austria

March 11, 2019• Physics 12, 27

3D maps of a sample’s refractive index—used in some biomedical tests—can be directly derived from angle-dependent measurements of light scattering from the sample.

Figure caption — **Figure 1:** Sketch of the refractive index mapping method demonstrated by Fiore et al. [4]. The method is based on using a confocal microscope to image light scattered from the sample in two geometries. (a) In the 0 geometry, the incident and scattered photons are normal to the sample interface. (b) In the $𝛼$ geometry, the incident and scattered light have an average angle $𝛼$ with respect to the normal to the surface. Since both geometries probe the same phonon direction (q), the measured Brillouin frequency shift—which depends on the internal light angle ( $𝛽$ )—can be related to the refractive index at the focal spot.

The refractive index is the most important macroscopic optical property of a material. It determines the effective wavelength of light traveling inside the material and the trajectory that such light will trace. Manipulating the refractive index can alter the path of light in surprising ways (as seen, for instance, in optical metamaterials) [1] or dramatically change the behavior of embedded emitters [2]. Its relevance, however, extends beyond light manipulation: The refractive index can be related to the mass density and to the mechanical and electrical properties of a medium. This relationship makes the refractive index a useful biomarker for studying biological cells. By measuring the refractive index in a sample, researchers can diagnose diseases like malaria or characterize key properties of single biological cells [3]. Antonio Fiore at the University of Maryland, College Park, and co-workers have now demonstrated a novel label-free approach for mapping the refractive index of samples with high spatial resolution in 3D [4]. The method exploits the angle-dependent interaction of light with inherent thermal vibrations (phonons) present in a sample. Compared to existing solutions, the new method provides a direct measurement of the refractive index without requiring any knowledge or assumptions about the sample geometry and optical properties.

Measuring the refractive index of a reasonably transparent bulk material is not too difficult. Through Snell’s law, the index can be deduced from angle-resolved refraction measurements of incident light. The Abbe refractometer, first realized over a century ago [5], remains a gold standard for these measurements. This and similar refractive approaches, however, are not suitable for mapping the refractive index with high, 3D spatial resolution in complex heterogeneous samples like cells. Over the last 50 years, researchers have developed a multitude of techniques to tackle such samples. These include methods based on optical interference (such as quantitative phase imaging) [6], on the placement of cells inside resonant optical cavities [7], or on the measurement of the fluorescent lifetime of markers embedded in the cell [8].

Existing techniques, however, come with a number of limitations. For instance, they may require prior knowledge of sample geometry, rely on certain assumptions about the material’s optical properties, or require comparison measurements with reference values, all of which may not be easy to do for complex samples. They are also often subject to so-called phase-wrapping artifacts—false reconstructed patterns of refractive index that result when phase variations of the imaging light inside the sample are large or not smooth. The approach proposed by Fiore and colleagues potentially overcomes some of these limitations by providing a more direct way to measure the refractive index through the interaction of light with sound waves. The new technique is based on a spectroscopic method called spontaneous Brillouin light scattering. This method involves probing a sample with a single-frequency laser and measuring the light that’s scattered from the sample inelastically, that is, with a different frequency than the incoming laser. This inelastic scattering signal results from the coupling of light to acoustic phonons [9].

In a typical Brillouin experiment, one observes two inelastic peaks in the scattered light, called the Stokes and anti-Stokes peaks, which are slightly shifted in frequency around the main elastic scattering peak. Given the low energy of the acoustic phonon modes, the two peaks will be spectrally very close to the elastic scattering peak, with a typical shift on the order of $\sim 10$ GHz when probing biological samples at optical wavelengths. This frequency shift, which is proportional to the velocity of the probed acoustic phonon, can be thought of as a manifestation of the Doppler shift: It results from light being scattered by the moving phonon.

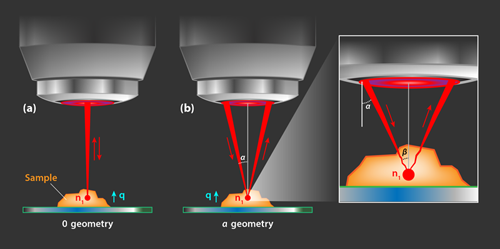
The key idea behind the authors’ approach is that the refractive index of the sample can be mapped by probing Brillouin scattering in two geometries. The first is a backscattering geometry, or 0 geometry, in which the direction of the incident and scattered photons are approximately opposite [Fig. 1 (a)]. In the second configuration, or $𝛼$ geometry, the incident and scattered light are each, on average, at an angle of $𝛼$ with respect to the normal to the surface. [Fig. 1 (b)]. The shift of the Brillouin peaks in the $𝛼$ geometry, $Ω_{𝛼}$ , is different from the shift in the 0 geometry, $Ω_{0}$ . The authors derive analytical expressions for these shifts showing that both configurations probe acoustic phonons propagating along the same axis. Their calculations reveal a relation between the ratio of the shifts, $R = Ω_{𝛼} ∕ Ω_{0}$ , and the refractive index in the volume probed at the focal point:

n = {[\frac{{sin}^{2} 𝛼}{1 - R^{2}}]}^{1 ∕ 2} .

Therefore, by measuring the Brillouin shifts, the team is able to directly extract the refractive index within the volume in which the photons are scattered.

Fiore and his colleagues implement this approach within a scanning confocal microscopy setup. Confocal microscopy produces 3D images by sequentially performing measurements at a focal spot that is scanned through the volume of a sample. Using a system of shutters and flip mirrors, the researchers can rapidly switch between measuring Brillouin scattering in the 0 and the $𝛼$ geometry. And they use a “virtually imaged phase array spectrometer” to measure the small shifts, $Ω_{0}$ and $Ω_{𝛼}$ , in rapid succession. To validate their approach, they show they can acquire precise spatial 3D maps of the refractive index of a drop of a photo-activated polymer deposited on a petri dish.

The authors demonstrate a spatial resolution of several micrometers for all three dimensions. When imaging an actual sample, the resolution will depend on the degree of overlap of the foci for the two probing directions (0 and $𝛼$ ), which may prove particularly challenging to control deep inside samples with significant refractive index variations. In such cases, one could envision the use of additional tunable corrective optics to assure consistent focus overlap. Employing other tricks like larger numerical apertures and different lens configurations, the authors suggest that a spatial resolution below one micrometer could be achieved in all dimensions. Improving the spatial resolution, however, may affect the accuracy with which the Brillouin spectra can be measured, which in turn reduces the precision in determining the refractive index. As the authors indicate, this reduction could be mitigated by performing measurements over more than two angles, but that would likely bring additional alignment (foci overlap) challenges. Ultimately, one would need to find a compromise between experimental complexity and desired refractive index precision and spatial resolution.

Despite the present complexity of the setup, future improvements in Brillouin spectrometers may lead to a wider implementation of the conceptually elegant approach demonstrated by the authors. Since this approach is label-free (i.e., it does not require adding fluorescent markers or other markers), it will be particularly appealing for bioimaging and diagnostic applications. As such, it may be applied to analyze cellular mass density behavior related to cancer development or to corneal pathologies, for instance.

This research is published in Physical Review Letters.

References

H. Chen, C. T. Chan, and P. Sheng, “Transformation optics and metamaterials,” Nat. Mater. 9, 387 (2010).
E. M. Purcell, “Resonance absorption by nuclear magnetic moments in a solid,” Phys. Rev. 69, 681 (1946).
P. Y. Liu et al., “Cell refractive index for cell biology and disease diagnosis: past, present and future,” Lab Chip 16, 634 (2016).
A. Fiore, C. Bevilacqua, and G. Scarcelli, “Direct three-dimensional measurement of refractive index via dual photon-phonon scattering,” Phys. Rev. Lett. 122, 103901 (2019).
E. Abbe, Neue Apparate zur Bestimmung des Brechungs - und Zerstreuungsvermögens fester und fluüssiger Körper (Mauke's Verlag, Jena, 1874).
Y. Park, C. Depeursinge, and G. Popescu, “Quantitative phase imaging in biomedicine,” Nat. Photon. 12, 578 (2018).
X. J. Liang, A. Q. Liu, C. S. Lim, T. C. Ayi, and P. H. Yap, “Determining refractive index of single living cell using an integrated microchip,” Sens. Actuators A 133, 3354 (2007).
C. Tregidgo, J. A. Levitt, and K. Suhling, “Effect of refractive index on the fluorescence lifetime of green fluorescent protein,” J. Biomed. Opt. 13, 031218 (2008).
B. J. Berne and R. Pecora, Dynamic Light Scattering With Applications to Chemistry, Biology, and Physics (Dover Publications Inc., Mineola, 2000)[Amazon][WorldCat].

About the Author

Kareem Elsayad heads the Advanced Microscopy team at the Vienna Biocenter Core Facilities (VBCF) in Vienna, Austria, where he and his team develop optical microscopy and spectroscopy techniques that are offered to biologists and medical researchers at a core facility based at VBCF. After a Ph.D. in condensed-matter physics, Kareem’s interests have focused on exploiting light-matter interactions to extract previously inaccessible information from biological systems. His research has broadly contributed to the fields of microscopy, high-resolution optical spectroscopy, and nanophotonics. Kareem currently chairs the EU funded “BioBrillouin” network, whose goal is to bring Brillouin light-scattering spectroscopy closer to applications in life science and medicine.