Plot Thickens in Solar Opacity Debate
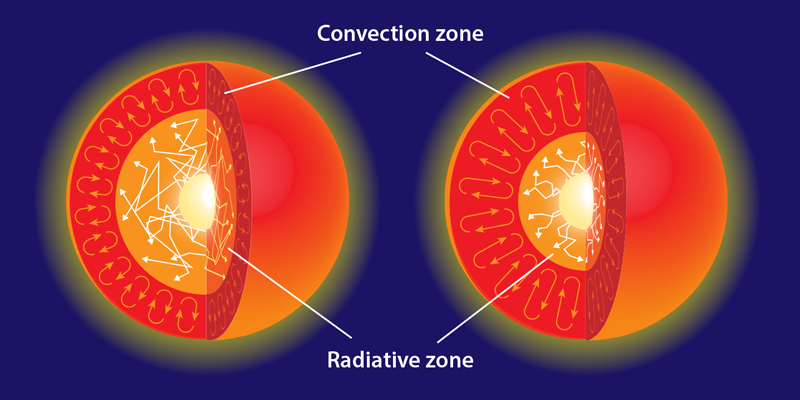
Our understanding of the Sun and other stars is based on models of the motion of energy inside hot, dense environments. Energy produced in stellar cores must pass through large amounts of ionized material—or plasma—to reach the star’s surface where it is radiated away. This energy transport can occur in two ways: through radiation or through convection. How efficiently energy is transferred by radiation and where radiation gives way to convection depends on how opaque the stellar plasma is. The opacity contribution from particular elements used in stellar models are the result of complex calculations [1], which are difficult to test directly. However, recent progress at the Z machine at Sandia National Laboratories in New Mexico has made it possible to observe plasmas under stellar conditions—albeit for small amounts of material and for short times. Taisuke Nagayama, from Sandia Labs, and colleagues have now used the Z facility to measure opacities due to iron, chromium, and nickel at the high densities and temperatures found in the solar interior [2]. They found large discrepancies between the measured and modeled opacities, implying that stellar opacity calculations are far from correct. The results may mean our understanding of the Sun and stars is less clear than we thought.
The challenge in testing stellar opacity calculations is that we cannot easily reproduce the conditions present inside a star, short of exploding a thermonuclear bomb. In previous work, researchers have employed an indirect test based on the boundary in the Sun where energy transport switches from radiation to convection (Fig. 1). Predicting the location of this boundary, which sits at the base of the convection zone, depends in large part on what opacity values we insert into our solar models. And we can check if those inputs are correct by comparing with helioseismology observations. Helioseismology, which is the study of oscillatory motion in the gas at the Sun’s surface, can reveal the internal structure of the Sun to an amazing degree of precision in a model-independent manner [3]. In particular, helioseismology observations tell us that the radiation-convection boundary occurs at , where is the solar radius [4]. If solar models have the wrong opacity inputs, then they will not be able to reproduce the boundary location coming from helioseismology measurements.
But this is where the story becomes complicated. Stellar opacities depend on two components: the intrinsic opacity of a particular element and the number of atoms and/or ions of that element that are contained in a star. The latter is quantified by a parameter called the “metallicity,” which is the abundance of heavy elements relative to the amount of hydrogen. The stellar astrophysics community is currently in disagreement about the solar metallicity, with older measurements giving a high metallicity [5] and newer measurements offering a significantly lower value [6]. When combined with the intrinsic opacities from calculations, the older metallicity value results in solar models that match helioseismic constraints very well. By contrast, the newer metallicity value does not give a match [7]. So which is wrong: the new metallicity measurement or the calculated opacities that go into the models? To settle this debate, we need a way to measure intrinsic opacities directly.
It was at the Z facility in 2015 that the first direct measurements of intrinsic opacities were made under conditions resembling those in the Sun [8]. In this experiment, a thin foil of iron was illuminated with x rays generated by a megajoule electromagnetic pulse, causing the sample to heat up to two million kelvin. At these temperatures, the iron atoms ionized, forming a short-lived dense plasma. Spectrometers recorded the x rays passing through the plasma in the wavelength range 7.0–12.7 Å . By estimating how much light at each wavelength was blocked, researchers determined the opacity of the plasma. The results showed that the intrinsic opacity of iron was higher than expected, which would imply that we need to rethink photon absorption calculations in high-temperature plasma. The plasma at the base of the Sun’s convection zone contains a variety of ionized iron species, but the dominant iron ion is one that has lost 17 of its electrons, leaving it with just two electron shells: a full K shell and an L shell with one vacancy. If the 2015 Z experiments were right, then theorists must have misestimated the strength of the electronic transitions of the L-shell electrons in highly ionized iron.
However, to be sure that there’s a problem with the calculations, the experimentalists need to confirm their results with follow-up observations. Nagayama et al. repeated the measurements for iron, and they also measured the opacity of chromium and nickel, which have similar electronic configurations to iron. Nickel has a full L shell under the same conditions, while chromium has three vacancies. If the problem with modeling opacities is due to L-shell transitions, then one would expect the theory-experiment discrepancy to be lowest for nickel and highest for chromium. Nagayama et al. confirmed the iron opacity from the 2015 experiment, showing that the older results are reproducible. However, what is more interesting is that—contrary to expectations—the theory-experiment discrepancy was highest for iron rather than for chromium. This iron anomaly is particularly glaring at low wavelengths that are far away from spectral lines. The opacity is supposed to be easier to calculate in regions without lines, but even in these no-line regions, the iron calculations appear to underestimate the opacity. By contrast, the chromium and nickel calculations match observations, which seems to rule out a simple explanation in which the discrepancy depends on the atomic number or electron count.
Of course, merely knowing that there are discrepancies does not help us much, unless we understand the missing physics that is causing the discrepancies. The 2015 results had stirred the atomic physics community into revisiting the issue of opacities [9]. A number of ideas were put forward, such as including lesser-known photon absorption processes, but this was before the added complications from these new results, which have made the opacity issues more…opaque. Theorists therefore have their work ahead of them but so do experimentalists, as the Sun is full of other light-absorbing elements to consider. Oxygen and neon produce, respectively, 25–27% and 10–13% of the opacity at the solar convection-zone base compared to iron’s 15–20% contribution. In order to have a more complete picture of solar opacities, future experiments will need to figure out how to construct samples made with oxygen and neon gases. We will probably have to wait a while longer until we can determine how opaque solar material really is.
This research is published in Physical Review Letters.
References
- C. A. Iglesias and F. J. Rogers, “Updated opal opacities,” Astrophys. J. 464, 943 (1996); N. R. Badnell, M. A. Bautista, K. Butler, F. Delahaye, C. Mendoza, P. Palmeri, C. J. Zeippen, and M. J. Seaton, “Updated opacities from the Opacity Project,” Mon. Not. R. Astron. Soc. 360, 458 (2005); G. Mondet, C. Blancard, P. Cossé, and G. Faussurier, “Opacity calculations for solar mixtures,” Astrophys. J. Suppl. 220, 2 (2015).
- T. Nagayama et al., “Systematic study of L-shell opacity at stellar interior temperatures,” Phys. Rev. Lett. 122, 235001 (2019).
- S. Basu, “Global seismology of the Sun,” Living Rev. Sol. Phys. 13, 2 (2016); S. Basu, M. H. Pinsonneault, and J. N. Bahcall, “How much do helioseismological inferences depend on the assumed reference model?,” Astrophys. J. 529, 1084 (2000).
- J. Christensen-Dalsgaard, D. O. Gough, and M. J. Thompson, “The depth of the solar convection zone,” Astrophys. J. 387, 413 (1991); S. Basu and H. M. Antia, “Seismic measurement of the depth of the solar convection zone,” Mon. Not. R. Astron. Soc. 287, 189 (1997).
- N. Grevesse and A. J. Sauval, “Standard solar composition,” Space Sci. Rev. 85, 161 (1998).
- M. Asplund, N. Grevesse, A. J. Sauval, and P. Scott, “The chemical composition of the sun,” Annu. Rev. Astron. Astrophys. 47, 481 (2009).
- S. Basu and H. M. Antia, “Helioseismology and solar abundances,” Phys. Rep. 45, 217 (2008); “Revisiting the issue of solar abundances,” J. Phys. Conf. Ser. 440, 012017 (2013).
- J. E. Bailey et al., “A higher-than-predicted measurement of iron opacity at solar interior temperatures,” Nature 517, 56 (2014).
- Proceedings of Workshop on Astrophysical Opacities, 2017, edited by Claudio Mendoza, Sylvaine Turck-Chiéze, and James Colgan, ASP Conference Series, Vol. 515 (Astronomical Society of the Pacific, San Francisco, 2018)[Amazon][WorldCat].