Questioning a Universal Law for Electron Attenuation
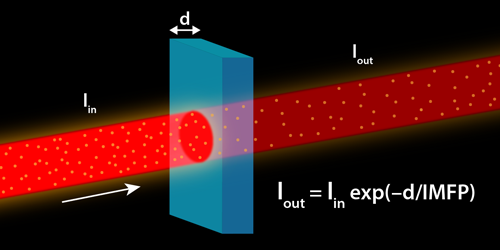
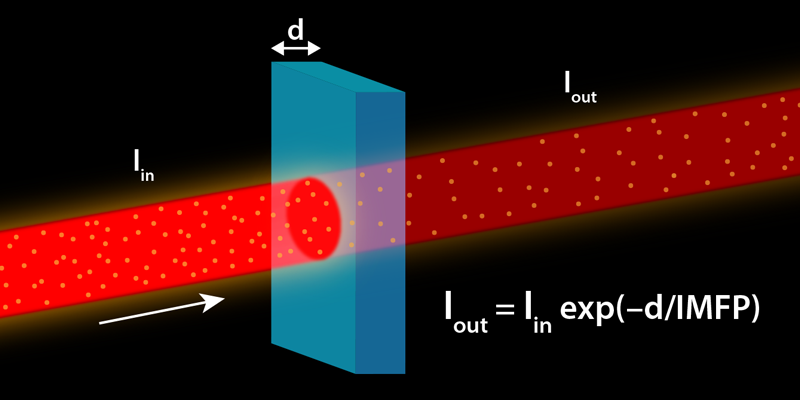
In nanoscale science and technology, the ability to measure an object’s dimensions with nanometer accuracy is of paramount importance. The most precise tool for determining the lateral dimensions of patterns on a surface is scanning probe microscopy. Along the vertical coordinate, dimensions can be inferred using the fact that an incoming electron beam is attenuated depending on a material’s thickness (Fig. 1). For the past 50 years, researchers have thought that a universal law could be used to convert electron-attenuation factors into thicknesses for a broad range of electron energies (see note in Ref. [1]). The law, however, has barely been tested for low energies (1–50 eV)—a range of increasing scientific and technological importance. Now Daniël Geelen at Leiden University in the Netherlands and co-workers have characterized the propagation of electrons through multilayer graphene at these energies, showing clear deviations from the expected universal behavior [2]. Their analysis indicates that electron-beam attenuation is significantly affected by the band structure of the solid and is thus material dependent. The result will benefit the quantitative understanding of many techniques employing low-energy electron beams, including photoemission, microscopy, diffraction, and electron-beam lithography.
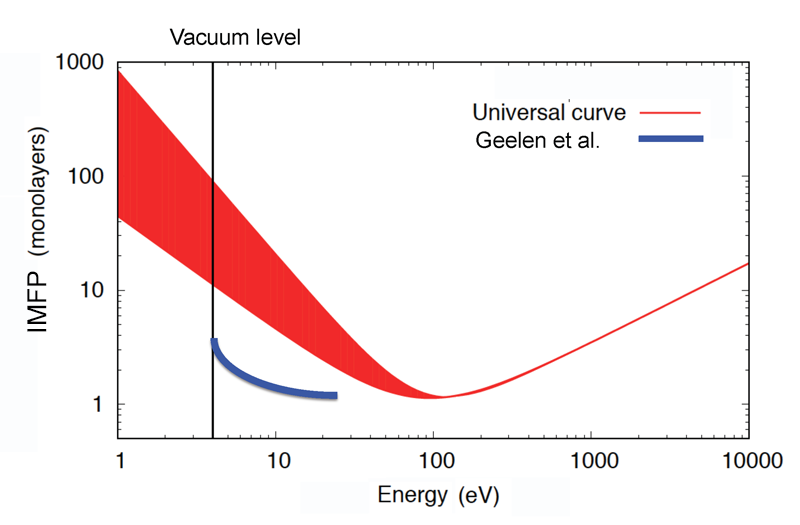
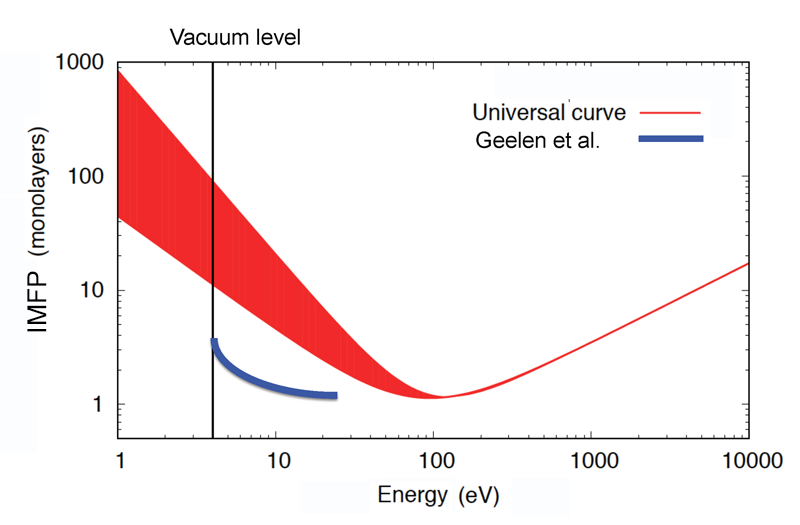
The universal law relates the energy of the electrons to the electron inelastic mean-free path (IMFP)—the average length over which the electron travels before losing energy in a scattering event. In 1979, two researchers compiled data on the electron attenuation length (see note in Ref. [3]) and concluded that the IMFP follows a universal curve, with a negligible dependence on the specific material [4]. According to their law, this characteristic length hits its minimum value—about one atomic layer—at around 50 eV (Fig. 2). This behavior reflects the energy dependence of different mechanisms for electron-energy loss. The excitation of phonons and transitions between the solid’s electronic bands dominates in the low-energy range. The coupling to collective modes (plasmons) plays an important role at slightly higher energies, setting the minimum around 50 eV. Above 50 eV, the IMFP increase reflects, loosely speaking, the reduction in the interaction time: Faster electrons have less time to be scattered by the sample.
As shown in Fig. 2., the IMFP remains shorter than a few hundred atomic layers over a vast energy range (1 to 10,000 eV), which is why electron-beam attenuation is such a sensitive measure of thickness. Researchers agree on the values to be used for energies above ∼100 eV [5], and they have widely adopted a 2015 formula describing the IMFP energy dependence above ∼50 eV [6]. For energies lower than 50 eV, however, a large uncertainty still exists (Fig. 2), mostly attributable to two causes. The first is a severe dearth of experimental data in this energy range—working with eV electrons is challenging because they are hard to focus and their trajectories can be affected by small magnetic fields in the environment, including Earth’s field. Futhermore, the IMFP is hard to measure because it is so small and experiments require carefully controlled samples. The second is the fact that, from a theoretical standpoint, it’s unclear how to treat the damping of collective plasmon oscillations at these energies [7].
Geelen and co-workers were able to characterize the propagation of low-energy electrons through multilayer graphene (one to four atomic layers). Building on recent technological advances, the team used a transmission electron microscope (TEM) and a previously developed low-energy electron microscope [8] to measure, respectively, the transmitted and reflected intensity of electrons impinging on the samples with energies between 4 and 25 eV. From such intensities, they derived not only the IMFP but also the elastic mean-free path—the average length over which electrons are scattered without losing energy. Their measured values for the IMFP are almost 10 times lower than those that would be predicted using the universal law.
This deviation from universality is similar to that hinted by data from a 2013 study [8], which were based on electron reflection only. However, by characterizing the elastic mean-free path through simultaneous reflection and transmission measurements, the authors could delve into the reasons behind this behavior. Strikingly, they found that the elastic mean-free path, at certain energies, exhibits strong peaks where it increases by over 1 order of magnitude.
To understand the elastic mean-free-path contribution, the author modeled the material’s transmission using a toy model from optics, in which multilayer graphene is described as a sequence of layers with a certain transmission and reflection coefficient at each layer boundary. The toy model convincingly reproduced the data, suggesting that the peaks in the elastic mean-free path occur when electrons reflected by the multiple layers interfere destructively, which maximizes transmission and leads to a longer mean-free path.
The toy model clearly points at interference phenomena. To shed more light on the microscopic mechanisms behind this interference, the authors modeled the elastic and inelastic propagation of electrons with a full quantum-mechanical approach. Their calculations showed that the observed behavior is due to the interlayer resonances of multilayer graphene, which arise from the interference of electrons bouncing between adjacent layers. At energies matching these resonances, electrons move easily through the material, making it act as an antireflection coating. Outside of the resonant bands, electrons cannot propagate and get reflected, which reduces the mean-free path. This conclusion implies that the material’s band structure at a few electron volts strongly influences electron transport. Since the band structure is obviously material dependent, this leads to deviations from the universal curve. The results also imply that the very concept of a mean-free path—derived within classical Boltzmann statistics—needs to be revisited to include quantum-mechanical interference between electronic wave functions.
These findings may be important for many scientific and technological applications. One example is extreme ultraviolet (EUV) lithography, the next-generation technology for printing computer circuits. The spatial precision of this technique depends on the IMFP of low-energy electrons produced when EUV photons illuminate the lithographic resist. The result could also be useful at particle storage rings (such as the Large Hadron Collider), where researchers are evaluating the use of graphite layers to mitigate the emission of low-energy electrons due to synchrotron radiation hitting the walls of the accelerator cavities. This emission adversely affects the ring operation by forming an electron cloud. The present study may suggest new avenues for tackling such problems.
This research is published in Physical Review Letters.
References
- Previous work hinted at a nonuniversal material dependence above 100 eV. However, this weak material dependence can be modeled by adding material-specific parameters to the universal curve that do not result in significant changes in the shape of the curve. See Refs. [5] and [6].
- D. Geelen, J. Jobst, E. E. Krasovskii, S. J. van der Molen, and R. M. Tromp, “Nonuniversal transverse electron mean free path through few-layer graphene,” Phys. Rev. Lett. 123, 086802 (2019).
- The attenuation length (AL) is a physical quantity that’s generally different from the IMFP since it accounts for the fact that one or more elastic processes may alter the shape of a trajectory in between successive inelastic collisions. The AL is therefore typically smaller than the IMFP. See Ref. [2] for a discussion.
- M. P. Seah and W. A. Dench, “Quantitative electron spectroscopy of surfaces: A standard data base for electron inelastic mean free paths in solids,” Surf. Interface Anal. 1, 2 (1979).
- C. J. Powell and A. Jablonski, “Evaluation of calculated and measured electron inelastic mean free paths near solid surfaces,” J Phys. Chem. Ref. Data 28, 19 (1999).
- H. Shinotsuka, S. Tanuma, C. J. Powell, and D. R. Penn, “Calculations of electron inelastic mean free paths. X. Data for 41 elemental solids over the 50 eV to 200 keV range with the relativistic full Penn algorithm,” Surf. Interface Anal. 47, 871 (2015).
- H. T. Nguyen-Truong, “Electron inelastic mean free path at energies below 100 eV,” J. Phys. Condens. Matt. 29, 215501 (2017); C. T. Chantler and J. D. Bourke, “Low-energy electron properties: Electron inelastic mean free path, energy loss function and the dielectric function. Recent measurements, applications, and the plasmon-coupling theory,” Ultramicroscopy 201, 38 (2019); O. Y. Ridzel, V. Astašauskas, and W. S. M. Werner, “Low energy (1–100 eV) electron inelastic mean free path (IMFP) values determined from analysis of secondary electron yields (SEY) in the incident energy range of 0.1–10 keV,” J. Electron Spectrosc. Relat. Phenom. (2019).
- R. Zdyb, T. O. Mente, A. Locatelli, M. A. Niño, and E. Bauer, “Inelastic mean free path from reflectivity of slow electrons,” Phys. Rev. B 87, 075436 (2013).