Microdrop Concentrates Light Modes

Qi-Tao Cao; Yun-Feng Xiao

Viewpoint

Microdrop Concentrates Light Modes

State Key Laboratory for Mesoscopic Physics and Frontiers Science Center for Nano-optoelectronics, School of Physics, Peking University, Beijing, China

August 31, 2020• Physics 13, 134

Tiny oil droplets levitated in optical tweezers can host several hundred light modes with similar energies, a feature that could be exploited for sensing and telecommunications.

Figure caption — **Figure 1:** Carmon and co-workers fabricated a spherical microresonator with more than 200 degenerate modes of light [1]. To prepare the resonator, they levitated an oil droplet (grey sphere) in an optical tweezer (pink). The degenerate modes are distinguished by their azimuthal numbers $m$ , with different values of $m$ corresponding to different distributions of the optical field along the polar direction.

An atom in isolation has rotational symmetry, resulting in it having two or more distinct electronic states with the same energy. But place the same atom in a magnetic field that points, for example, north, and this energy “degeneracy” is lifted—a response known as the Zeeman effect, which can be used to measure magnetic field strengths with high precision. Like atoms, optical materials can support two or more degenerate states, or modes, of light if they are fashioned into symmetrical shapes, such as a ring, cylinder, or sphere. The degenerate states in these microresonators underlie many applications, such as unidirectional lasers, optical sensors, and gyroscopes. Now, Tal Carmon of the Technion-Israel Institute of Technology and collaborators demonstrate optical microresonators that are so close to being perfect spheres that they have more than 200 nearly degenerate modes [1]. The devices, which the researchers produced by levitating oil droplets in light, could lead to new possibilities in atomic optics, high-speed optical communications, and quantum information processing.

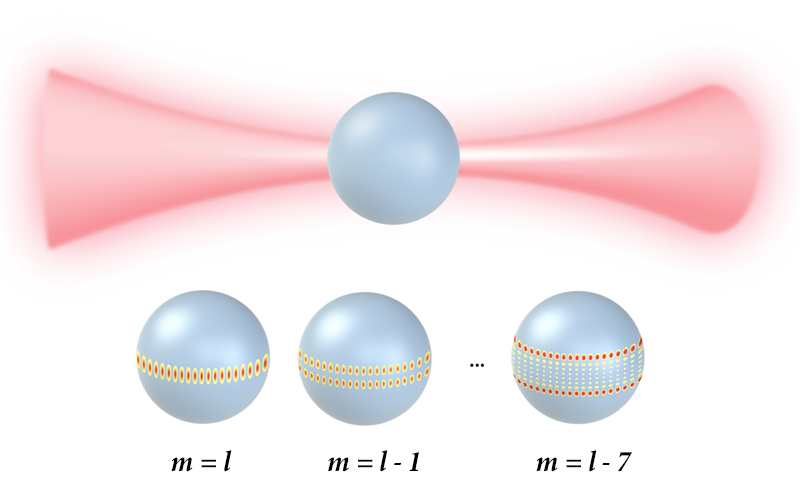
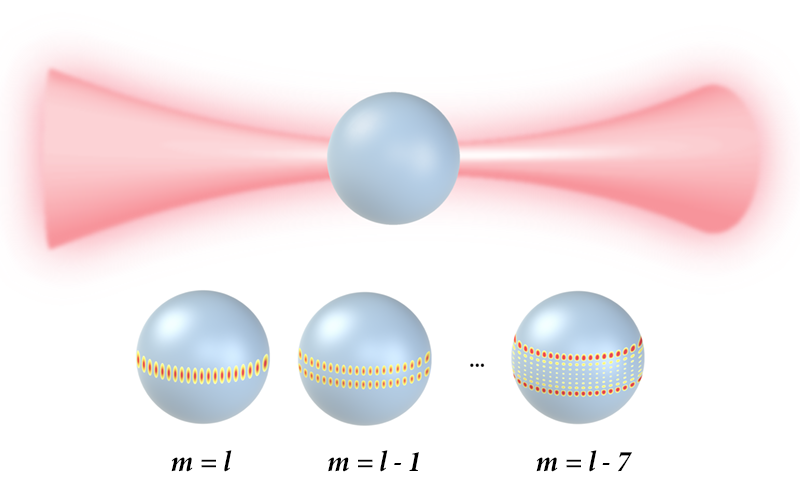
An optical microsphere resonator is made from a high-refractive-index material [2]. As such, light entering the device tends to stay confined and to keep circulating near the device’s interior surface because of total internal reflection. For certain frequencies, the optical path for light circulating in the resonator will be an integer multiple of the light’s wavelength, producing constructive interference. These discrete resonant modes (Fig. 1) are known as whispering gallery modes (WGMs) [3, 4], in reference to the acoustic “whispers” that are known to bounce long distances around the curved walls of St. Paul’s Cathedral in London. By design, WGM resonators have very smooth walls and contain few impurities, so that the modes stay confined for a long time. They also pack a lot of light into a small space, a property that researchers have used to study enhanced light-matter interactions.

Like the energy levels in an atom, the allowed modes in a WGM resonator with spherical symmetry are characterized by a set of integers: the radial number $n$ , the angular number $l$ , and the azimuthal number $m$ , where $m$ ranges from $- l$ to $l$ . These numbers indicate how the peak intensity of an optical mode is distributed in the sphere; for instance, $n = 1$ and $l = | m |$ corresponds to a uniform ring of light around the equator of the sphere. The resonant frequency (or energy) of a WGM depends on both the radial and angular numbers, but it is independent of the azimuthal number in a perfectly spherical resonator [5, 6]. As a result, a mode with a given $n$ and $l$ will possess ( $2 l + 1$ ) degenerate modes (Fig. 1). Since the value of $l$ that produces a resonant condition depends on the ratio of the resonator circumference and the light’s wavelength, spherical resonators that are tens of micrometers around can have hundreds of degenerate modes for visible or near-infrared light. In previous work, researchers studied solid spherical resonators of this size. But the resonators were supported by a pillar or other structure that distorted their spherical shape, both lifting the mode degeneracy and destroying the vast majority of these modes [5].

By rethinking the way a resonator is made and supported, Carmon and collaborators succeeded in seeing the full 200-fold degeneracy (hyperdegeneracy) expected for a 10- $𝜇 m$ -sized resonator [1]. They made the resonator out of a droplet of dielectric liquid (silicone oil) and gently levitated it in a focused beam of laser light called optical tweezers, in which radiation pressure provides a trapping and supporting force [7] (see Focus: Nobel Prize—Lasers as Tools). The tweezers almost perfectly preserve a droplet’s spherical symmetry. The droplet surface is also clean and smooth at the atomic level. As a result, the droplet has an extremely high quality factor ( $\sim 1 0^{9}$ )—a measure of the typical mode lifetime in the droplet.

To observe the modes, the researchers measured the spectrum of light transmitted through the resonator. This measurement entailed placing a tapered fiber next to (but not touching) the sphere and sending tunable, near-infrared laser light through the fiber. Light from the fiber was then transferred into and out of the sphere through an evanescent coupling. The resonant modes appeared in the transmission spectrum as sharp dips, whose depth and width can be analyzed to determine the quality factor and other optical properties.

While Carmon and co-workers observed all 200 expected modes, the modes were slightly spread in energy because the droplets are ever so slightly oblate. This small asymmetry—corresponding to about a 0.001% difference between the long and short axes—comes from a combination of the tweezer radiation pressure, gravity, and the coupled fiber. (In fact, without this asymmetry, all of the modes would have overlapped, and the researchers would have needed to “squash” the sphere to see how many modes were there.) Significantly, the team showed that all of the modes in their experimental spectra can be successfully predicted with a quantitative theory.

As a mesoscopic analog to a single atom, levitated microresonators could serve as well-controlled platforms for simulating atomic optics. For instance, researchers could use the lifted degeneracy of the azimuthal modes to simulate the effects of gauge fields on degenerate atomic levels. Hyperdegenerate resonators may also trigger ideas on the applications front. One possibility is sensing. The frequency of hyperdegenerate modes is extremely sensitive to external perturbations, and even a tiny external perturbation—such as a biomolecule near the resonator surface—could lead to measurable modulation of the WGMs [8]. An analysis of this modulation would provide multidimensional information about the source of the perturbation. Another potential application is high-capacity optical communications [9], for which modes with different azimuthal numbers ( $m$ ) could be used to generate densely packed information channels. In this case, the control of the droplet’s shape would provide a way to dynamically modulate the intensity or phase of each channel.

Looking beyond classical communications, single-photon versions of the $l$ or $m$ states produced by the resonator could carry information as qubits for high-dimensional quantum information processing. Finally, Carmon and colleagues imagine a fascinating, albeit challenging, possibility, which is to design malleable optical circuits out of a series of levitated microresonators. Using newly available tools for controlling multiple tweezers in 3D, one could dynamically adjust the geometry and position of the resonators to make different kinds of optical circuits.

References

J. Kher-Alden et al., “Microspheres with atomic-scale tolerances generate hyperdegeneracy,” Phys. Rev. X 10, 031049 (2020).
M. L. Gorodetsky et al., “Ultimate Q of optical microsphere resonators,” Opt. Lett. 21, 453 (1996).
K. J. Vahala, “Optical microcavities,” Nature 424, 839 (2003).
H. Cao and J. Wiersig, “Dielectric microcavities: Model systems for wave chaos and non-Hermitian physics,” Rev. Mod. Phys. 87, 61 (2015).
L. Yang and K. J. Vahala, “Gain functionalization of silica microresonators,” Opt. Lett. 28, 592 (2003).
A. Chiasera et al., “Spherical whispering-gallery-mode microresonators,” Laser Photonics Rev. 4, 457 (2009).
A. Ashkin and J. M. Dziedzic, “Observation of resonances in the radiation pressure on dielectric spheres,” Phys. Rev. Lett. 38, 1351 (1977).
Y. Zhi et al., “Single nanoparticle detection using optical microcavities,” Adv. Mater. 29, 1604920 (2017).
P. Marin-Palomo et al., “Microresonator-based solitons for massively parallel coherent optical communications,” Nature 546, 274 (2017).

About the Authors

Qi-Tao Cao is a postdoctoral researcher at Peking University in China. He received his B.S. in physics from the University of Science and Technology of China in 2015 and his Ph.D. in physics from Peking University in 2020. His interest is in theoretical and experimental ultrahigh-quality-factor optical microcavity photonics, which includes microcavity nonlinear optics, symmetry breaking optics, and quantum optics.

Yun-Feng Xiao received his B.S. and Ph.D. in physics from the University of Science and Technology of China in 2002 and 2007, respectively. After postdoctoral research at Washington University in St. Louis, he joined the faculty of Peking University in 2009, where he was promoted to tenured associate professor in 2014 and to full professor in 2019. His research interests lie in the fields of microcavity photonics, including quantum and nonlinear optics, asymmetric resonant cavities and wave chaos, and microcavity optical sensing. He is an Optical Society of America Fellow and has served on the organizing committee for more than 30 international conferences.