A Precise Parity-Violation Measurement in Light Nuclei

Matthias R. Schindler; Roxanne P. Springer

Viewpoint

A Precise Parity-Violation Measurement in Light Nuclei

Matthias R. Schindler¹ and Roxanne P. Springer²

¹Department of Physics and Astronomy, University of South Carolina, Columbia, SC, USA
²Department of Physics, Duke University, Durham, NC, USA

September 23, 2020• Physics 13, 149

A new measurement from the

n^{3}

He Collaboration advances understanding of parity violation in few-nucleon systems.

Figure caption — **Figure 1:** In the neutron capture reaction used in the experiment, an incoming neutron with spin in the direction $ŝ_{n}$ is captured by a helium-3 nucleus, resulting in a tritium nucleus and an outgoing proton propagating in the direction ${\hat{k}}_{p}$ . The correlation $ŝ_{n} \cdot {\hat{k}}_{p}$ violates parity gives the asymmetry $A_{PV}$ .

When studying parity violation in nuclei, it is a truth universally acknowledged that what is experimentally easy to measure is theoretically difficult to calculate, and what is theoretically easy to calculate is experimentally difficult to measure. Now, Michael Gericke of the University of Manitoba in Canada and colleagues have helped address this challenge by precisely measuring the rate of parity violation for a nuclear reaction that is within reach of theoretical understanding—neutron capture by helium-3 nuclei [1]. This measurement helps bring us closer to an understanding of how nucleons interact.

What is parity violation and why does it matter? A parity transformation replaces a three-dimensional coordinate system with one in which all directions are switched to their negatives. For example, a vector $\vec{r} = (1, 1, 1)$ in Cartesian coordinates transforms under a parity operation into $- \vec{r} = (- 1, - 1, - 1)$ . Because a vector $\vec{r}$ transforms in this way, we say that it has negative parity. Angular momentum, on the other hand, does not change sign under a parity operation because $\vec{L} = \vec{r} \times \vec{p}$ . Both $\vec{r}$ and $\vec{p}$ have negative parity and change sign under a parity transformation, so their cross product $\vec{L}$ has positive parity.

Once nuclear physics was understood to be governed by a few fundamental forces of nature, scientists assumed that those forces remained invariant under parity transformations because no parity violation had been observed in past experiments. However, in 1956, Tsung-Dao Lee and Chen-Ning Yang pointed out that parity invariance had not been experimentally tested for the weak interactions [2]. Within months, Chien-Shiung Wu and colleagues observed parity violation in cobalt-60 nuclei [3] (see Focus: Landmarks—Breaking the Mirror). Today, researchers continue to study parity violation not only to refine our understanding of nuclear phenomena but to potentially probe for new physics.

To look at parity violation in a simpler system, consider the neutrino. Assuming the neutrino is massless, which is sufficient for the purposes of this discussion, its spin always points in the direction opposite to its momentum’s direction. As discussed above, momentum $\vec{p}$ changes sign under a parity transformation, but angular momentum—including spin—does not. If a neutrino is traveling in the $+ \hat{z}$ direction with spin pointed in the $- \hat{z}$ direction, a parity transformation would take it to a neutrino traveling in the $- \hat{z}$ direction with spin in the $- \hat{z}$ direction. But such a particle does not exist! We say that parity is maximally violated by neutrinos. (Taking into account the tiny finite neutrino mass just makes this parity violation slightly less than maximal.)

Things are not so simple, however, in nuclear systems, because parity violation in nuclei arises from an interplay between strong and weak forces. The nucleons—neutrons and protons—that form nuclei consist of quarks and gluons. Both the binding of nucleons into nuclei and the behavior of quarks and gluons inside nucleons are governed by the strong force. Unfortunately, quantum chromodynamics (QCD), the theory of strong interactions, is complicated to calculate at nuclear energies. This makes it very difficult to understand how QCD is manifest in nuclei. QCD itself is invariant under parity, but quarks are also subject to weak interactions, which violate parity. Studying parity violation in nuclei with high precision can serve as a potent window into the inner workings of nucleons.

But weak interactions have their name for a reason—the parity-violating component of the nucleon-nucleon interactions is 7 orders of magnitude smaller than the parity-conserving component. On the experimental side, this makes the signal of parity violation very tiny compared to background effects. So the general strategy is to find observables that would vanish if parity were conserved. Instead of trying to find a tiny effect on top of something much larger, the goal is to find a deviation from zero.

In some special cases, parity-violating signals in nuclei can be enhanced by several orders of magnitude to make measurements easier, but these enhancements can only happen in large nuclei. Unfortunately, a detailed theoretical description of large nuclei using QCD-based calculations is currently out of reach. The fewer the nucleons involved, the easier it is to connect the calculations to QCD. This is one reason why the measurement of a parity-violating asymmetry in the capture of cold neutrons by helium-3 is such an important development.

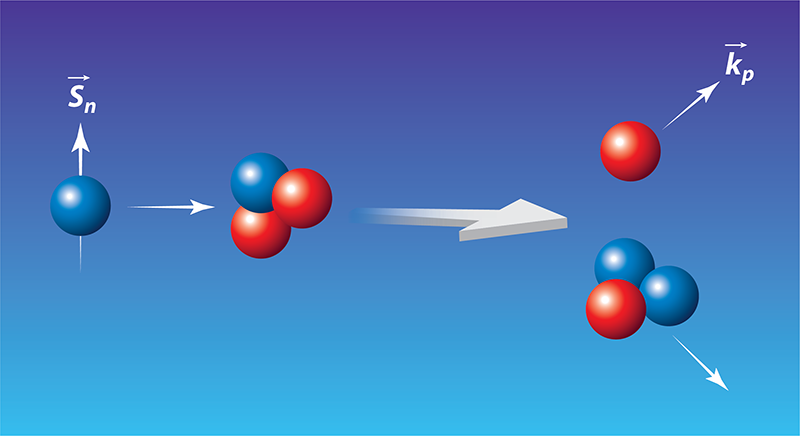
In the helium-3 experiment [1], Gericke and colleagues of the $n^{3}$ He Collaboration used the Spallation Neutron Source (SNS) at Oak Ridge National Laboratory to shoot a beam of neutrons along the $\hat{z}$ direction. The neutrons, with spins aligned perpendicularly to the direction of their propagation ( $\pm ŷ$ ), enter the helium-3 target chamber, which also serves as the detector. In the reaction of interest, a neutron collides with a helium-3 nucleus ( $^{3} He$ ), yielding an outgoing proton and a tritium nucleus ( $^{3} H$ ). Measuring how often this process occurs as a function of the proton’s propagation direction and then correlating it with the neutron spin direction determines the parity-violating asymmetry $A_{PV}$ . If parity were conserved, the detector would see an identical distribution of protons in its upper and lower halves, and $A_{PV}$ would be zero. But parity was violated in this reaction, so the protons were not evenly distributed. The measured asymmetry was $A_{PV} = 1.55 \times 1 0^{- 8}$ with a statistical uncertainty of $0.97 \times 1 0^{- 8}$ and a systematic uncertainty of $0.24 \times 1 0^{- 8}$ .

The reported precision is better than that of any previously measured few-nucleon system. To give an example of the level of care the researchers took to achieve this result: The orientation of one of the elements in their detector (a wire frame) had to be measured to within 3 milliradians.

This precision of the $A_{PV}$ measurement was also made possible by the very low background in the helium-3 target chamber, improvements in controlling the spin-flipping of the incoming neutrons, and analysis advancements in understanding SNS beam fluctuations and detector acceptance.

The result from the $n^{3}$ He Collaboration is a spectacular achievement. Its impact is best seen in the larger landscape of parity-violating nuclear forces and interactions. Parity violation is so complex in nuclei that no single experiment provides sufficient information; a suite of observables must be analyzed to understand the phenomena. There are very few nuclei that are both well understood theoretically and well measured experimentally. It is when the results of the $n^{3}$ He and other experiments—the NPDGamma experiment [4], the polarized proton-proton scattering experiment [5], and future few-nucleon experiments—are combined with a robust, QCD-based, theoretical understanding [6] that we can start to disentangle the interplay of the fundamental forces in the nucleons. Theory advances—in the use of effective field theories that encode the symmetries of QCD in the language of nucleons, and in numerical simulations of QCD—will continue to complement the experimental efforts. Eventually, understanding QCD and its interplay with other forces in nuclear systems will enable us to use nuclei to search for hints of new particles and new forces that are beyond the standard model.

Correction (5 October 2020): We felt it was important to clarify that the physicist Chien-Shiung Wu was behind the observation of parity violation in cobalt-60.

References

M. T. Gericke et al. (n3He Collaboration), “First precision measurement of the parity-violating asymmetry in cold neutron capture on $^{3} He$ ,” Phys. Rev. Lett. 125, 131803 (2020).
T. D. Lee and C. N. Yang, “Question of parity conservation in weak interactions,” Phys. Rev. 104, 254 (1956).
C. S. Wu et al., “Experimental test of parity conservation in beta decay,” Phys. Rev. 105, 1413 (1957).
D. Blyth et al., “First observation of $P$ -odd $𝛾$ asymmetry in polarized neutron capture on hydrogen,” Phys. Rev. Lett. 121, 242002 (2018).
P. D. Eversheim et al., “Parity violation in proton-proton scattering at 13.6 MeV,” Phys. Lett. B 256, 11 (1991).
M. Viviani et al., “Chiral effective field theory analysis of hadronic parity violation in few-nucleon systems,” Phys. Rev. C 89, 064004 (2014).

About the Authors

Matthias Schindler is an associate professor at the University of South Carolina. He obtained his Ph.D. from the Johannes Gutenberg University Mainz, Germany, and held postdoctoral positions at Ohio University and the George Washington University, Washington D.C. His research focuses on the use of effective field theories and symmetries in light nuclei.

Roxanne P. Springer is a professor of physics at Duke University, North Carolina. She obtained her Ph.D. from the California Institute of Technology and is a fellow of the American Physical Society. She has expertise in effective field theories of quantum chromodynamics and weak interactions.