Shining a Light on Hidden Spin Dynamics

Darío A. Arena

Viewpoint

Shining a Light on Hidden Spin Dynamics

Department of Physics, University of South Florida, Tampa, FL, USA

September 24, 2020• Physics 13, 151

Researchers combine ferromagnetic resonance with x-ray reflectivity to map out the complex spin behavior of a magnetic multilayer.

Figure caption — **Figure 1:** Burn and co-workers used a technique that combines x-ray resonant magnetic scattering and ferromagnetic resonance. A static magnetic field aligned with the z axis, and an alternating magnetic field orthogonal to it ( $H_{RF}$ ), cause electron spins in the multilayer to precess. Meanwhile, a polarized and pulsed x-ray beam, which is synchronized with the spin precession, meets and reflects from the multilayer. By varying the angle of the x rays and the phase ( $Δ 𝜑$ ) between $H_{RF}$ and the x-ray pulses, Burn and co-workers map out the precession phase throughout the multilayer.

Since the first ghostly, skeletal image that Wilhelm Röntgen created of his wife’s hand, the remarkable ability of x rays to reveal hidden objects has become commonplace. Moreover, thanks to synchrotrons, today’s x-ray techniques can reveal much more than an object’s shape. At these facilities, the wavelength of x rays can be tuned precisely to enhance x-ray absorption and reflection at energies that coincide with the atomic binding energies of electrons in different elements. Such resonant scattering and absorption provides experimentalists with the powerful ability to peer into complex materials and dissect the contributions from those elements. Synchrotrons also provide a few other experimental knobs to tweak—allowing, for example, selection of the polarization of the x rays and rapid pulsing of the x-ray bunches. Now, David Burn, of the Diamond Light Source in the UK, and colleagues have assembled these different components into a method that reveals the complicated and inhomogeneous spin dynamics in a magnetic multilayer [1]. Such multilayered structures will play a crucial role in the new field of spintronics, allowing devices that store and process information based on electrons’ spins.

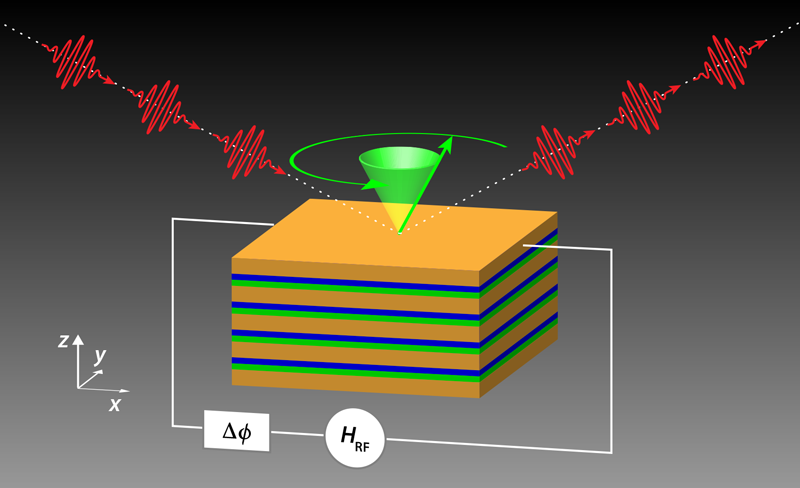
The experimenters combine two powerful spectroscopic techniques—x-ray resonant magnetic scattering (XRMS) and ferromagnetic resonance (FMR). Previous studies have succeeded in characterizing the spin dynamics in simpler, two-layer magnetic structures [2–4]. The combination of XRMS and FMR, however, permits Burn and colleagues to probe a magnetic multilayer in which the dynamics of spins across the different layers may interact in a more complex fashion. The sample they study comprises a stack of four sequences of CoFeB/MgO/Ta. CoFeB is a “soft” ferromagnetic alloy, MgO is an insulator, and Ta is a relatively heavy metal that stabilizes a variety of spin textures. The dissimilar MgO/CoFeB and CoFeB/Ta interfaces can support a variety of such spin textures with intriguing topological properties [5]. The main question addressed by Burn and co-workers is whether each individual CoFeB layer exhibits the same spin dynamics under FMR excitation.

In effect, XRMS is an x-ray reflection technique that combines x-ray scattering with absorption spectroscopy to probe the distribution of a particular magnetic element. The resonant and magnetic aspects of XRMS arise from an approach called x-ray magnetic circular dichroism spectroscopy. This method exploits the fact that the spin of circularly polarized x-ray photons couples to the spin of tightly bound core electrons, preferentially exciting electrons of one spin species. In ferromagnets (materials with a net spin), differences in the valence spin density of states lead to differences in the absorption probability of x rays whose circular polarization is aligned or antialigned with the sample’s net magnetization. This absorption asymmetry produces large variations in the reflectivity of the sample as a function of the photon energy, allowing the spin direction to be measured with elemental resolution.

The element that Burn and colleagues focus on is Fe, which they achieve by setting the photon energy to $\sim 708 eV$ —the Fe $L_{3}$ edge, where Fe $2 p_{3 ∕ 2}$ electron states exhibit strong transitions. XRMS is used to analyze different depths within the structure by rotating the sample beneath the x-ray beam while an x-ray detector measures the beam’s specular reflection. When the beam grazes the surface of the sample, the reflected signal carries information about the shallowest layers of the structure. At higher angles of incidence, the beam probes further into the sample’s interior.

While XMRS can reveal variations in the magnetic profile of a sample, conventional FMR provides detailed information about its average magnetic properties. In this technique, a static magnetic field ( $H_{Bias}$ ) is used to saturate the sample’s magnetization while a small alternating field ( $H_{RF}$ )—generally orthogonal to $H_{Bias}$ —excites precessional motion of the electron spins. The multilayer’s out-of-plane magnetic anisotropy allows Burn and colleagues to orient $H_{Bias}$ perpendicularly to the plane of the structure, causing the material’s electron spins to precess in a cone with its axis at right angles to the sample’s surface (Fig. 1).

The FMR precession is generally very fast (in the GHz frequency range for most ferromagnets) and the quick oscillations would smear out to their average value under a conventional, time-averaged detection scheme. Burn and co-workers implement a phase-sensitive detection mode to overcome this limitation. X rays arrive in short bunches with a repetition frequency of $\sim 500 MHz$ at many modern synchrotrons. By phase locking $H_{RF}$ to the 4th harmonic of the synchrotron’s $500 - MHz$ pulse-repetition frequency, the researchers use XRMS to stroboscopically sample the magnetization, which oscillates at 2 GHz, at the same point in each precession orbit. They map out the complete orbit by shifting the relative phase ( $Δ 𝜑$ in Fig. 1), which is equivalent to introducing a varying time delay between $H_{RF}$ and the x-ray bunch clock. The resulting XRMS intensity oscillates sinusoidally as a function of the phase difference.

If the precession throughout the CoFeB/MgO/Ta multilayer were uniform, there would be no variation in the phase of the XRMS oscillations as a function of the x-ray scattering angle (a proxy for depth). It would be like four children on adjacent playground swings, all moving in unison. Instead, Burn and co-workers observe large deviations in the phase as the scattering angle is increased. Their modeling of the dynamic scattering indicates that the relative phase of the precession shifts by $5^{\circ}$ from one CoFeB layer to the next. This amounts to a significant $1 5^{\circ}$ phase lag between the top and bottom CoFeB layers. The variation of the phase between adjacent magnetic layers suggests that the excitation mode in the multilayer is nonuniform; its motion is a type of pseudo-spin-wave throughout the depth of the structure. In this case, the four children move in a more serpentine fashion, with one in the lead and the others following but always slightly behind in their motion.

A similar type of phase variation in different ferromagnetic layers has been observed previously in magnetic bilayers [2–4, 6, 7], and FMR coupled with XRMS has been implemented in geometries with in-plane magnetization [8–10]. The advance by Burn and co-workers has been to fully map out the relationship between precession phase and depth in the small-cone-angle regime, in which the precession cone angle varies linearly with $H_{RF}$ amplitude. This enables detailed modeling of the spin dynamics throughout the CoFeB/MgO/Ta multilayer stack.

Looking forward, the acquisition of detailed scattering information can be extended to look for phase-sensitive, off-specular scattering signals along axes within the plane of the multilayer. Such measurements will be challenging because of the low intensity of off-specular scattered x rays. They may reveal collective excitations of topologically complex spin textures such as skyrmion lattices or spin solitons/domain walls, and they might also be used to detect propagating spin waves. Characterizing these phenomena will be an important step toward delivering novel spintronic applications, in which interactions between skyrmions and similar spin structures could form the basis for memory, logic gates and, perhaps, quantum-computing operations.

References

D. M. Burn et al., “Depth-resolved magnetization dynamics revealed by x-ray reflectometry ferromagnetic resonance,” Phys. Rev. Lett. 125, 137201 (2020).
P. Klaer et al., “Element-specific ferromagnetic resonance in epitaxial Heusler spin valve systems,” J. Phys. D. Appl. Phys. 44, 425004 (2011).
W. E. Bailey et al., “Detection of microwave phase variation in nanometre-scale magnetic heterostructures,” Nat. Commun. 4, 2025 (2013).
Y. Pogoryelov et al., “Nonreciprocal spin pumping damping in asymmetric magnetic trilayers,” Phys. Rev. B 101, 054401 (2020).
W. Li et al., “Anatomy of Skyrmionic Textures in magnetic multilayers,” Adv. Mater. 31, 1807683 (2019).
D. A. Arena et al., “Weakly coupled motion of individual layers in ferromagnetic resonance,” Phys. Rev. B 74, 064409 (2006).
T. Martin et al., “Layer resolved magnetization dynamics in interlayer exchange coupled ${Ni}_{81} {Fe}_{19} ∕ Ru ∕ {Co}_{90} {Fe}_{10}$ by time resolved x-ray magnetic circular dichroism,” J. Appl. Phys. 103, 07B112 (2008).
W. E. Bailey et al., “Precessional dynamics of elemental moments in a ferromagnetic alloy,” Phys. Rev. B 70, 172403 (2004).
S. Buschhorn et al., “Adaption of a diffractometer for time-resolved X-ray resonant magnetic scattering,” J. Synchrotron Radiat. 18, 212 (2010).
S. Buschhorn et al., “Precessional damping of Fe magnetic moments in a FeNi film,” J. Phys. D. Appl. Phys. 44, 165001 (2011).

About the Author

Darío A. Arena received his Ph.D. in experimental surface physics from Rutgers University, New Jersey. After postdoc work at Lawrence Livermore National Laboratory, California, and the Naval Research Laboratory, Washington D.C., he was employed as a physicist and beam line scientist at Brookhaven National Laboratory, New York, specializing in x-ray spectroscopy of magnetic materials. He is a Fulbright Scholar and is currently an Associate Professor at the Department of Physics at the University of South Florida. His research interests are in nanomagnetism and spin dynamics.