Geometry Rescues Superconductivity in Twisted Graphene
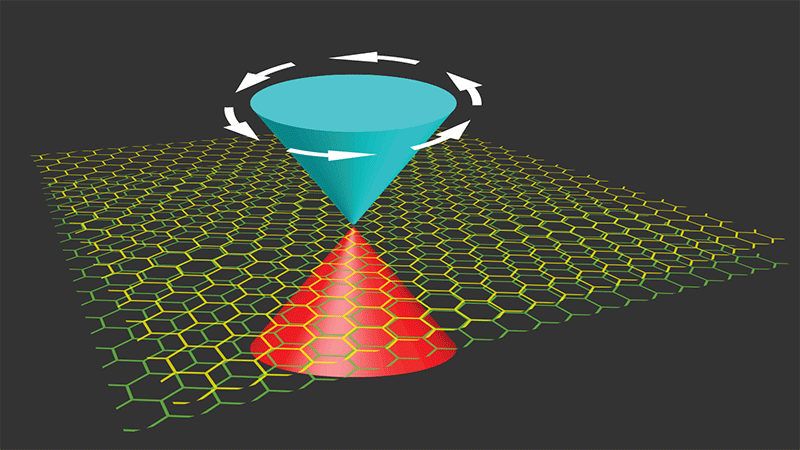
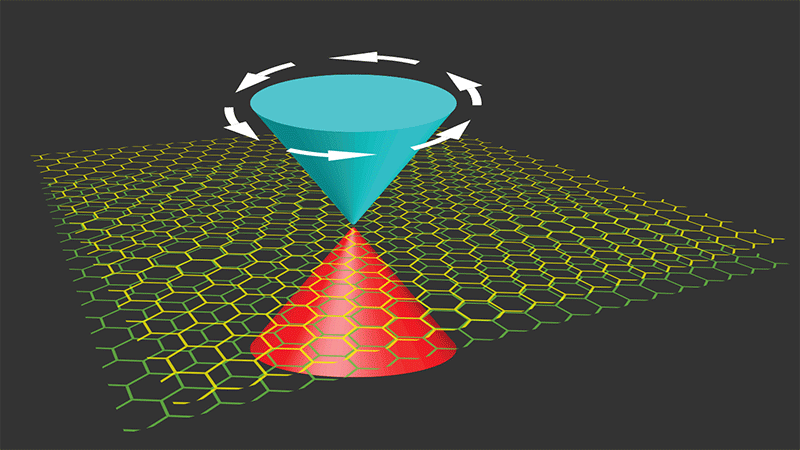
On its own, a sheet of graphene is a semimetal—its electrons interact only weakly with each other. But as experimentalists discovered in 2018 [1, 2], the situation changes when two sheets of graphene are stacked together, with a slight ( ∼ 1°) rotation between them (Fig. 1). At this so-called magic twist angle [3] and at low temperatures [1], the electrons become correlated, forming insulating or superconducting phases depending on the carrier density [2–7]. These phases appear to come from a twist-induced flattening of the electronic energy bands, which narrows the electrons’ range of kinetic energies relative to their interaction energy. Researchers are actively trying to understand the twist-induced phases—for example, whether the superconductivity is ordinary or something more exotic. In a trio of papers, three independent theoretical groups contribute to this effort. They show that the value of the superconducting transition temperature in twisted bilayer graphene (TBG) is much higher than expected because of the special geometry of its electronic wave functions [8–10]. This so-called geometric contribution would persist even if TBG’s energy bands could be made perfectly flat, a condition where superconductivity would disappear in most materials.
Superconductivity describes the state of a material that has zero electrical resistance and expels magnetic fields. An important characteristic of the superconducting state is its superfluid weight—a quantity whose value can be thought of as the “strength” of the superconductivity. In a (quasi-)2D system like TBG, the superfluid weight is directly related to the superconducting transition temperature (also referred to as the Berezinskii-Kosterlitz-Thouless temperature).
Within this context, the superconducting transition temperature of magic-angle TBG presents a mystery at first blush. It’s known that in relatively simple metals with a single-band, the superfluid weight is proportional to the bandwidth. So flat bands, like the ones TBG has, should mean a low superfluid weight, and a correspondingly low transition temperature. But TBG can exhibit a transition temperature of up to 3 K, which, scaled to its Fermi temperature, is among the highest known [2]. Why is this temperature so high?
The answer to this question, according to the new work, lies in two features of TBG’s band structure. First, it comprises several bands, not just one. Second, it has special “Dirac” points, where two linearly dispersing bands touch (Fig. 1). These points are singularities in the band geometry, and their existence leads to a "geometric" contribution to the superfluid weight. Several years ago, theorists (including authors of one of the new papers [9]) demonstrated that the superfluid weight in a multiband material can be divided into two contributions: the conventional one, which is zero for a perfectly flat band, and the geometric one, which is connected to interband processes [11, 12]. The geometric contribution can remain finite in a flat band because the lower bound on its value arises from the band geometry.
The three groups have taken the step of connecting this multi-band, geometric effect to TBG [8–10]. Building on the earlier work [11, 12], Fang Xie from Princeton University and colleagues show that there is indeed a lower bound on the superfluid weight for TBG that comes from the band geometry and is given by a topological invariant [8]. Specifically, because of TBG’s crystal symmetry, the states near the Dirac points have a very particular momentum dependence. This dependence reveals an inherent geometric property of the states and shows up as a curvature (Berry curvature) that can be represented by a vector that winds around the Dirac points (Fig. 1); the topological invariant characterizes this winding. The Berry curvature may sound abstract, but it makes a real contribution to an observable quantity by contributing to the superfluid weight. As a consequence, TBG’s transition temperature can be high even with perfectly flat bands. In other words, the transition temperature is not limited by the available kinetic energy—highlighting a qualitative difference between TBG and conventional superconductors.
All three groups based their calculations on similar inputs. They adopted the same effective continuum description of twisted bilayer graphene that was used in 2011 to predict the existence of magic angles [1]. Furthermore, they used a mean-field model for superconductivity that assumes an isotropic pairing interaction and results in an isotropic superfluid weight. In their study, Aleksi Julku of Aalto University in Finland and colleagues went a step further and employed a second model that incorporates a nearest-neighbor pairing interaction [9]. When this interaction is sufficiently strong, it leads to a form of superconductivity where rotational symmetry is broken (nematic superconductivity) and a superfluid weight that is anisotropic. Experimental efforts to detect this anisotropy might provide insight into the material’s much-debated pairing symmetry.
The three groups also analyzed how the superfluid weight varies as electrons or holes are added to the nearly flat bands [9, 10]. Xiang Hu of William & Mary, Virginia, and his colleagues argue that the superfluid weight’s evolution with this band filling depends on whether the geometric or conventional contribution dominates, providing a means to distinguish the two cases experimentally [10]. At the same time, they found that the ratio of the contributions depends on the twist angle, with the geometric part dominating at the magic angle.
The trio of papers shows that—in the flat-band limit—the geometry of the electronic band structure in TBG governs the superfluid weight and, in turn, the transition temperature. This direct relationship offers new insights into the nature of superconductivity and its connection to the band-structure topology in TBG. It also means that the superfluid weight can be used to study geometric effects experimentally. Whether experimentalists can reach the flat-band limit in TBG, however, is unclear. The bandwidths and transition temperatures measured so far place TBG in an intermediate regime, where the kinetic energy and electron-interaction energy are of the same order of magnitude. Julku et al. [9] and Hu et al. [10] showed that, in this case, the conventional contribution can still be sizable or even dominant.
Just two years after discovering correlated phases in TBG, the material presents many interesting questions: What is the pairing mechanism and what is the resulting symmetry of the gap? How do the results in the new papers [8–10] change if one considers other types of pairing symmetry or goes beyond-mean-field calculations? Is superconductivity affected by the insulating states? Also, twisted structures can be created with other materials and more layers: How strong is the geometric contribution in these systems?
It would be exciting if the experimentally accessible regime could be made “flatter,” that is, with more strongly interacting electrons. As the new papers show, the geometric contribution would dictate the behavior of the superconducting weight and “rescue” superconductivity. In this regime, the transition temperature could grow with the pairing interaction and lead to true strong-coupling superconductivity—an interesting prospect in the hunt for superconductors with higher transition temperatures.
This research is published in Physical Review B and Physical Review Letters.
Editor's Note (29 April 2020): In the original version of this article, Ref. [8] was an arXiv paper. This paper is now published in Physical Review Letters and the references and text have been updated accordingly.
References
- Y. Cao et al., “Unconventional superconductivity in magic-angle graphene superlattices,” Nature 556, 43 (2018).
- Y. Cao et al., “Correlated insulator behaviour at half-filling in magic-angle graphene superlattices,” Nature 556, 80 (2018).
- R. Bistritzer and A. H. MacDonald, “Moire bands in twisted double-layer graphene,” Proc. Natl. Acad. Sci. U.S.A. 108, 12233 (2011).
- M. Yankowitz et al., “Tuning superconductivity in twisted bilayer graphene,” Science 363, 1059 (2019).
- G. Chen et al., “Signatures of tunable superconductivity in a trilayer graphene moiré superlattice,” Nature 572, 215 (2019).
- X. Lu et al., “Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene,” Nature 574, 653 (2019).
- A. L. Sharpe et al., “Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene,” Science 365, 605 (2019).
- F. Xie et al., “Topology-bounded superfluid weight in twisted bilayer graphene,” Phys. Rev. Lett. 124, 167002 (2020).
- A. Julku et al., “Superfluid weight and Berezinskii-Kosterlitz-Thouless transition temperature of twisted bilayer graphene,” Phys. Rev. B 101, 060505 (2020).
- X. Hu et al., “Geometric and conventional contribution to the superfluid weight in twisted bilayer graphene,” Phys. Rev. Lett. 123, 237002 (2019).
- S. Peotta and P. Törmä, “Superfluidity in topologically nontrivial flat bands,” Nat. Commun. 6, 8944 (2015).
- L. Liang et al., “Band geometry, Berry curvature, and superfluid weight,” Phys. Rev. B 95, 024515 (2017).