Finding Spin Hedgehogs in Chiral Crystals
Much of modern technology is based on controlling the way electrons are transported through materials. One of the control knobs is the electron spin, which is utilized in spintronic devices. Spin offers an extra constraint on how electrons can move: to travel between states, an electron must have not only the correct energy but also the correct spin. Precisely what directions are open to the electron depend on the material’s spin texture—how its spins are arranged in momentum space. Now, for the first time, Masato Sakano, at the University of Tokyo, and colleagues have discovered a spin texture with a hedgehog pattern that prevents an electron from scattering backwards along its path and that also suppresses scattering in all other directions [1]. The effect should greatly influence the resistivity of a material—especially in a magnetic field—and might even be used to generate pure spin currents.
The spin texture observed by Sakano and colleagues is a special case in which all of the spins relevant to electron transport point away from or toward a point. Under this radial spin texture, an electron that could otherwise scatter freely across a constant-energy surface is forbidden from making a U-turn, and it also has a reduced probability of scattering in any other direction—there being no parallel spin state available. The researchers observed this spin texture in chiral crystals of pure tellurium (Te). Chiral crystals come in two mirror-symmetric forms, and Sakano et al. found that the handedness of the crystal determines whether the radial spins point inward or outward.
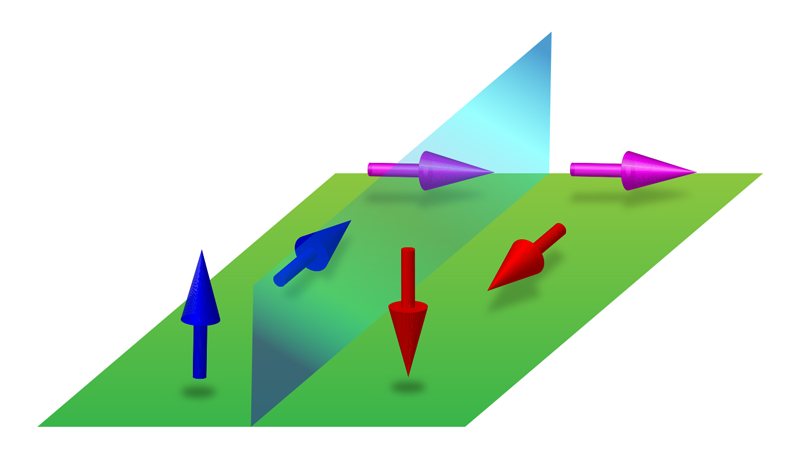
The range of spin textures that a crystal can adopt is constrained by the crystal’s symmetries and the way that each symmetry affects spin. Spin is a pseudovector, meaning that under a mirror operation, it undergoes a reflection followed by inversion of the spin direction (Fig. 1). A consequence of this property is that, in crystals with a mirror plane, spins on either side of the plane are flipped if they are plane-parallel, while those perpendicular to the plane remain the same. Close to the plane, therefore, only plane-perpendicular spins can exist, as plane-parallel spins necessarily fall to zero [2]. In nonmagnetic systems, possible spin textures are also determined by the more fundamental time-reversal symmetry, which is independent of the crystal structure and which dictates that spin is inverted when momentum is reversed at the same energy.
Additional constraints arise from the combination of time-reversal symmetry and inversion symmetry, which is a reflection through a point rather than a plane. In particular, a material that has both of these symmetries has spin-degenerate bands, meaning the spin imposes only a weak constraint on how electrons can move between different bands. To lift this degeneracy and therefore constrain electrons more strongly by spin, the inversion symmetry must be broken. This symmetry breaking can occur at an interface or in the bulk, although for given orientations, the resulting spin textures are identical [3]. Most crystal space groups with broken inversion symmetry still have mirror planes, yielding spin textures with nonradial components that wind around a central axis [4]. If the direction of the inversion symmetry breaking can be reversed—as is possible in a ferroelectric, for example, the opposite spin winding direction will arise [5].
From these symmetry considerations, it is clear that to create a purely radial spin texture, the crystal should lack inversion symmetry and have no mirror planes. This absence of symmetry is exhibited by chiral crystal structures, whose atomic arrangement resembles a spiral staircase. It has been known for many decades that pure Te crystallizes into such structures, but theoretical advances and improved experimental techniques revealed the full implications of this only recently.
All crystals that lack inversion symmetry show an enhanced spin-orbit effect, and this enhancement is even more pronounced in Te because of its high atomic number. Because of that, the spin splitting of the material’s bulk bands is large enough to be resolved directly using angle-resolved photoemission spectroscopy (ARPES) [6]. Going one step further and using spin- and angle-resolved photoemission spectroscopy (SARPES) [7], Sakano et al. were also able to measure the spin direction associated with particular bands, revealing the spin texture of the band structure close to the Fermi level. Measurement techniques like photoemission spectroscopy break time-reversal symmetry, causing effects that can obscure the material’s intrinsic, structurally determined spin texture. By considering the symmetry properties of the crystal structure, one can isolate these measurement artefacts [8]. The SARPES data obtained for a right-handed Te crystal show a clear hedgehog-like radial spin texture with the spins pointing away from the H point, a corner in the Brillouin zone (Fig. 2). In the left-handed crystal, the researchers found a reversal of the spin direction, leading to an inverted topology of the spin texture with all spins pointing towards the H point. (In Ref. [1], the team use the spin magnetic moment, which is opposite to the electron spin considered here.) Both the measurement of the purely radial spin texture and its inversion with chirality are the first of their kind and show again the strong coupling between electron spin and crystal symmetry.
The measured spin textures, their dependence on the handedness of the crystal, and the observation that all corners of the Brillouin zone have the same spin texture, have far-reaching consequences for the electromagnetic response of the material. The respective spin textures resemble the source or sink of a magnetic field and are thus reminiscent of a magnetic monopole in reciprocal space. When the Fermi level is shifted—for example by charge doping—this radial spin texture shrinks down to a singularity at the H point. Then, the spin points in all directions at once, which is equivalent to it no longer being spin polarized. Changing from a spin-polarized to a spin-degenerate state in this way would relax the spin constraint on electron transport. More exotic effects can be achieved by shifting the Fermi level even further into the unoccupied states where, according to theory, a topological phase of matter called a chiral Weyl semimetal should appear [9]. These prospects, and especially their experimental verification, will rely heavily on the findings by Sakano et al., whose work thus marks an important step in the development of novel spintronics applications based on chiral crystals.
This research was published in Physical Review Letters.
References
- M. Sakano et al., “Radial spin texture in elemental tellurium with chiral crystal structure,” Phys. Rev. Lett. 124, 136404 (2020).
- P. Höpfner et al., “Three-dimensional spin rotations at the Fermi surface of a strongly spin-orbit coupled surface system,” Phys. Rev. Lett. 108, 186801 (2012).
- Igor Žutić et al., “Spintronics: Fundamentals and applications,” Rev. Mod. Phys. 76, 323 (2004).
- G. Landolt et al., “Direct measurement of the bulk spin structure of noncentrosymmetric BiTeCl,” Phys. Rev. B 91, 081201 (2015).
- J. Krempaský et al., “Operando imaging of all-electric spin texture manipulation in ferroelectric and multiferroic Rashba semiconductors,” Phys. Rev, X 8, 021067 (2018).
- K. Nakayama et al., “Band splitting and Weyl nodes in trigonal tellurium studied by angle-resolved photoemission spectroscopy and density functional theory,” Phys. Rev. B 95, 125204 (2017).
- J. H. Dil, “Spin and angle resolved photoemission on non-magnetic low-dimensional systems,” J. Phys. Condens. Matter 21, 403001 (2009).
- J. H. Dil, “Spin- and angle-resolved photoemission on topological materials,” Electron. Struct. 1, 023001 (2019).
- M. Hirayama et al., “Weyl node and spin texture in trigonal tellurium and selenium,” Phys. Rev. Lett. 114, 206401 (2015).