Material Makes Photons Bulky
Nonlinear effects will be a crucial ingredient of future optical quantum information platforms. By allowing different information-carrying photons to interact, these effects can be useful for performing basic tasks like shifting the photons’ color, modifying their statistics, and inducing entanglement between them. Nonlinear processes are ubiquitous in laser optics, but in typical materials they are too inefficient to have a measurable effect at the single-photon level, as would be required for advanced quantum optics applications. Now, Li Bing Tan of the Swiss Federal Institute of Technology (ETH) in Zurich and co-workers report on a novel way to boost the optical nonlinearity of a medium [1]. Their idea is to couple, or “dress,” photons with suitable material excitations in an atomically thin semiconductor layer. The coupling results in quasiparticles called polaron-polaritons, which extend over large spatial scales and can interact surprisingly strongly with each other. The researchers’ measurements show that this coupling boosts the optical nonlinearity of the material by a factor of 50.
As we all learned in classical linear electrodynamics, two light beams do not feel each other’s presence as they intersect. The possibility of light-light scattering processes was first examined in the 1930s by physicists Werner Heisenberg and Hans Heinrich Euler, who predicted that two photons could interact through the exchange of virtual pairs of electrons and positrons. In vacuum, however, this nonlinear interaction is minuscule and hard to observe—its first evidence came only in 2017 [2]—because it occurs through the generation of virtual electron-positron pairs with large rest mass (MeV).
The situation is different when light propagates through a material whose dielectric polarization depends nonlinearly on the applied fields, if these fields are sufficiently strong. In a Heisenberg-Euler picture, this optical nonlinearity can be understood by replacing virtual electron-positron pairs with virtual electron-hole pairs, whose rest mass—determined by the electronic energy gap—is much lower than that of electron-positron pairs. The typical nonlinearity of materials is thus much higher than that of vacuum, but it remains quite small. It can be reinforced if the photon energy approaches an absorption band, but this comes at the price of reducing the efficiency of the nonlinear process and of destroying the quantum coherence between photons.
In the last twenty years, researchers have explored an alternative way to achieve nonlinearity by hybridizing photons with long-lived matter excitations like excitons—hydrogen-atom-like objects formed by the binding of an electron and a hole in a material. This hybridization produces a quasiparticle called a polariton, which can extend over many nanometers. It turns out that collisions between multiple polaritons boost nonlinearity. And, in a clean material, the fact that polaritons remain coherent results in little loss from absorption.
Research at the crossroad of optics, solid-state, and atomic physics [3] has tried to further boost these nonlinearities, exploring the coupling of light with other quasiparticles, from excitons with long-range dipolar interactions [4] to atomic Rydberg states [5]. The nonlinearities demonstrated so far are, however, insufficiently strong for many tasks. In particular, researchers can’t easily reach regimes in which a single photon can have a substantial effect on several other photons confined in a multimode optical cavity.
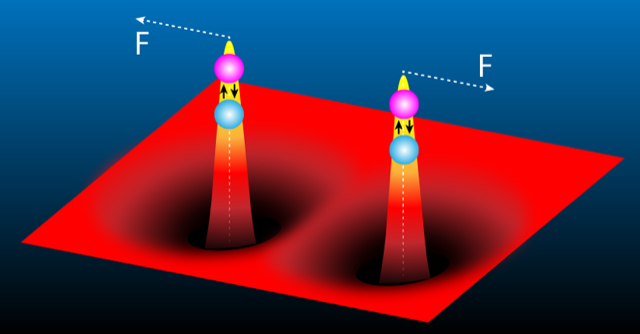
In a series of experiments, Tan and co-workers investigate a promising approach for boosting polaritonic nonlinearity. Their idea is to dress the polariton by coupling it to many-body excitations in a surrounding gas of electrons. In their system, the polariton consists of a photon strongly coupled to a tightly bound exciton in a monolayer of molybdenum diselenide. The electrons, injected from a gate electrode into the two-dimensional material, are attracted by the polaritons. As a result, the electron density has a peak close to the polariton but decreases over an extended circular ring around the peak (Fig. 1). The resulting quasiparticle, which combines the polariton with a redistribution of electrons, is known as a polaron-polariton (an analogy to the more familiar polarons that result from the distortion of the crystalline lattice around an electron in a solid). Compared to a pure polariton, the polaron-polariton is spatially much larger. This extension makes polarons interact at larger distances [6], which, as the experiments show, leads to a 50-fold boost in optical nonlinearity.
The team’s evidence for the enhanced nonlinearity comes from two observations. First, they see a characteristic signature of nonlinearity: the dependence of the refractive index on light intensity. This dependence is evident from shifts of the polaron-polariton resonance—a peak in light transmission through the sample occurring at a specific frequency. Second, they show that polaron-polaritons can be amplified through stimulated emission—the characteristic effect that underlies the operation of a laser. It is remarkable that this gain process amplifies not only the photonic part of the quasiparticle but also its polaronic part, made of the many-body distortion of the fermionic electron gas around each polariton.
As is, the observed nonlinearity is insufficient for quantum optics applications, and it is still inferior to that reported by previous studies by the same group [4]. But it might be enhanced in materials that have a higher intrinsic nonlinearity than molybdenum diselenide. With further improvements, the new approach might have a disruptive impact on quantum optics. First, it could push forward the study of strongly correlated quantum fluids of light, in which many photons are entangled with each other and behave like a quantum fluid. These fluids can mimic quantum phases of matter such as the Mott insulator, the Tonks-Girardeau gas, and the fractional quantum Hall state [6, 7]. Examples of such states have been created using microwave photons in circuit quantum electrodynamics, but demonstrations are so far limited to fluids with a small number of photons [8]. The approach of Tan and colleagues holds potential for scaling up to macroscopic fluids containing many photons.
Another compelling, albeit speculative, use of this approach is the search for anyons—quasiparticles following quantum statistics different from those of fermions or bosons. Anyons are predicted to form in two-dimensional electron systems and, under some conditions, they are expected to have non-Abelian quantum statistics. These exotic statistics could be harnessed to build powerful quantum computers with topological protection [9]. Experiments have observed intriguing hints of anyons in fractional quantum Hall materials, but the evidence is still not fully convincing. A scheme similar to that of Tan and co-workers could provide the smoking gun for these quasiparticles. The idea would be to bind polaritons to fractionally charged anyons in a quantum Hall material, thereby creating anyon-polaritons. As indicated by a recent theoretical study by my group, measurements of the scattering between two such anyon-polaritons could reveal the quantum statistics of these particles [10].
This research is published in Physical Review X.
References
- L. B. Tan et al., “Interacting polaron-polaritons,” Phys. Rev. X 10, 021011 (2020).
- M. Aaboud et al. (ATLAS Collaboration), “Evidence for light-by-light scattering in heavy-ion collisions with the ATLAS detector at the LHC,” Nat. Phys. 13, 852 (2017).
- D. E. Chang et al., “Quantum nonlinear optics — photon by photon,” Nat. Photon. 8, 685 (2014).
- E. Togan et al., “Enhanced interactions between dipolar polaritons,” Phys. Rev. Lett. 121, 227402 (2018).
- T. Peyronel et al., “Quantum nonlinear optics with single photons enabled by strongly interacting atoms,” Nature 488, 57 (2012).
- J. Tangpanitanon and D. G. Angelakis, “Many-body physics and quantum simulations with strongly interacting photons,” arXiv:1907.05030.
- I. Carusotto and C. Ciuti, “Quantum fluids of light,” Rev. Mod. Phys. 85, 299 (2013).
- I. Carusotto et al., “Photonic materials in circuit quantum electrodynamics,” Nat. Phys. 16, 268 (2020).
- C. Nayak et al., “Non-Abelian anyons and topological quantum computation,” Rev. Mod. Phys. 80, 1083 (2008).
- A. Muñoz de las Heras et al., “Anyonic molecules in atomic fractional quantum Hall liquids: a quantitative probe of fractional charge and anyonic statistics,” arXiv:2004.02477.