Postponing Heat Death in Periodically Driven Systems
Speaking of “nonequilibrium systems” is as specific as speaking of “nonelephant animals.” These systems are a diverse bunch, with a tendency for disorder and unpredictability. However, one particular class of nonequilibrium systems—those that are periodically driven—can exhibit order out of this mess. In recent years, mounting theoretical and experimental evidence has shown that periodic driving may be a key ingredient for engineering exotic quantum-mechanical states of matter, such as time crystals and room-temperature superconductors [1]. But a dark cloud has always loomed over this so-called Floquet engineering: the driving leads to heating and the heating kills the order. Antonio Rubio-Abadal from the Max Planck Institute for Quantum Optics in Germany and his colleagues have now explored a window of opportunity where such unwanted heating can be suppressed [2]. Their work motivates further efforts in Floquet engineering to produce new states of matter, such as topological states with no equivalent in the world of equilibrium physics.
In a sense, periodically driven systems occupy a space somewhere between “static” and “nonequilibrium.” The systems oscillate in time, but their behavior can be constant over timescales longer than the oscillation period. At the quantum level, this long-term constancy means the system can be described using an effectively static energy equation, called the Floquet Hamiltonian [1]. Interestingly, the Floquet Hamiltonian can be radically different from its static counterpart or indeed from any physically permitted static Hamiltonian. The Kapitza pendulum, for example, is driven at its suspension point, causing it to oscillate upside down—as though its bob had a negative gravitational mass. Ions trapped in oscillating fields can seemingly defy Maxwell’s equations.
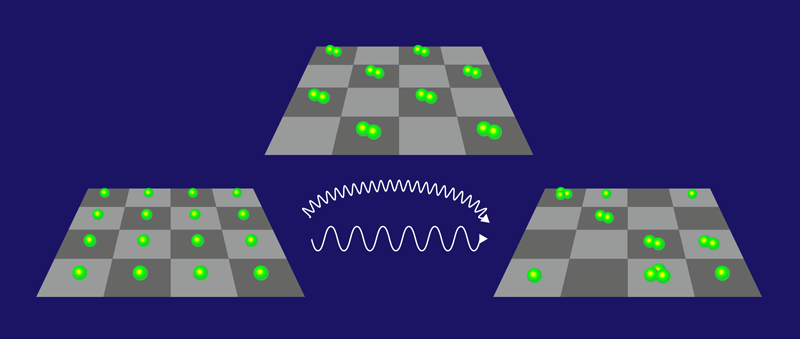
Periodically driven systems might also exhibit novel states of matter. Condensed-matter physicists are exploring the use of periodic driving as a tuning knob that could alter the properties of a material on ultrafast timescales [3]. Experiments have shown how driving with light can produce superconductivity and anomalous topological insulators. However, materials are complex systems that can be hard to control. For this reason, atomic physicists have developed simple models of solids using nanokelvin atomic gases loaded into optical lattices made of intersecting laser beams [4]. Using these “quantum simulators,” researchers have been able to explore the effects of periodic driving by literally shaking the atoms inside the lattices. Recent experiments have simulated a transition from a superfluid to a Mott insulator [5] and the generation of topologically nontrivial band structures [6]. Despite these successes, further progress in Floquet engineering has been hindered by heating: As atoms in an optical lattice are extremely well isolated from their environment, any absorption of energy from the shaking will eventually lead to a maximally disordered “heat death.”
The question is, how long until “eventually”? Can the inevitable heat death be delayed? Recent theoretical work has shown that going to a higher frequency—beyond the scale set by few-body dynamics—should cause an exponential decrease in the heating of a driven system [7]. Such a suppressed heating rate could allow a “prethermal regime” during which the system has time to thermalize within the effective Floquet Hamiltonian. This regime would offer researchers the chance to explore novel properties before their driven system is eventually overwhelmed by heating. Previous work has observed very low heating in a driven system [8], but Rubio-Abadal and colleagues have now provided a systematic study of heating suppression that reveals its exponential character [2].
The team studied a gas of bosonic atoms in one and two-dimensional optical lattices, and periodically modulated the lattice depth to drive the system. Observing an exponential change in the heating rate posed several experimental obstacles. For one, the researchers had to use a very sensitive thermometry technique to precisely measure the temperature of the atoms over a wide range of values. They also needed to control for heating caused by fluctuations in the laser beams and by collisions with atoms floating in the vacuum chamber (these residual particles remain despite the pressure in the chamber being 14 orders of magnitude below atmospheric pressure). By minimizing these backgrounds, the team was able to measure the effect of changing the frequency of the driving. They observed that the heating rate at high frequency was 100 times smaller than at low frequency, in agreement with expectations for the Floquet prethermal regime.
This heat suppression can be understood by taking into account a peculiarity of nature that gives quantum mechanics its name: In general, particles can only absorb energy in quantized amounts. When driving a system, the supplied energy is proportional to the driving frequency. And if that energy is too high, a single atom may not have any way of accommodating it. An ensemble of atoms that interact with each other could collectively absorb much higher energies. But it may require a complex rearrangement that has a low probability of happening and is therefore slow. Imagine that you are trying to give a dollar to each person in a group of one hundred people, but all you have is a one-hundred-dollar note. You will have to make a lot of small transactions to distribute the money.
It should be noted that the theoretical predictions for heating suppression were based on fermions, where arrangements are limited by the Pauli exclusion principle. By contrast, Rubio-Abadal and colleagues used bosonic atoms, where some uncertainty remained as to whether these predictions would hold. The fact that the researchers see heating suppression shows that this phenomenon is more universal than what could initially be proven.
Driving at higher frequencies is not a silver bullet. Certain elements within the Floquet Hamiltonian—corresponding to effects that researchers would like to observe—actually become smaller as the frequency increases. To counteract this reduction, researchers need to use stronger (larger amplitude) driving, which unfortunately increases heating. It is possible to avoid this zero-sum game by going to a high enough frequency, where the exponential suppression dominates the (polynomial) increase from the stronger driving. However, real solids exposed to high-frequency driving can absorb the energy in direct excitations of electrons to higher bands. Hence, successful implementations of Floquet engineering in solids [9, 10] have so far focused on relatively low-frequency driving with mid- or far-infrared light. Nevertheless, the bigger complexity also opens up an exciting opportunity: Solids are never completely isolated systems, so they can also get rid of some excess energy. If their heating rate can be suppressed to below their cooling rate, a Floquet-engineered state may persist indefinitely. Rather than merely delaying heat death, it could be abolished.
But before we get ahead of ourselves, it remains an open question how applicable the Floquet framework is to nonisolated systems. To answer that, optical lattices could make a decisive contribution. Such an experiment would be a formidable challenge, as the lattice-bound atoms would have to be coupled to a reservoir that is kept at a constant temperature. But atomic physicists are renowned for their ambitious pursuits.
This research is published in Physical Review X.
References
- T. Oka and S. Kitamura, “Floquet engineering of quantum materials,” Annu. Rev. Condens. Matter Phys. 10, 387 (2019).
- A. Rubio-Abadal et al., “Floquet prethermalization in a Bose-Hubbard system,” Phys. Rev. X 10, 021044 (2020).
- D. N. Basov et al., “Towards properties on demand in quantum materials,” Nat. Mater. 16, 1077 (2017).
- M. Lewenstein et al., Ultracold Atoms in Optical Lattices: Simulating quantum many-body systems (Oxford University Press, Oxford, 2012)[Amazon][WorldCat].
- A. Zenesini et al., “Coherent control of dressed matter waves,” Phys. Rev. Lett. 102, 100403 (2009).
- G. Jotzu et al., “Experimental realization of the topological Haldane model with ultracold fermions,” Nature 515, 237 (2014).
- D. A. Abanin et al., “Exponentially slow heating in periodically driven many-body systems,” Phys. Rev. Lett. 115, 256803 (2015).
- G. Jotzu et al., “Creating State-Dependent Lattices for Ultracold Fermions by Magnetic Gradient Modulation,” Phys. Rev. Lett. 115, 073002 (2015).
- Y. H. Wang et al., “Observation of Floquet-Bloch states on the surface of a topological insulator,” Science 342, 453 (2013).
- J. W. McIver et al., “Light-induced anomalous Hall effect in graphene,” Nat. Phys. 16, 38 (2019).