Getting a Handle on Timing
Some of the most enigmatic yet exciting problems in science involve electronic, atomic, and molecular processes that unfold on femtosecond ( 10−15s) timescales. Such processes range from the many-body, coherent dynamics of electrons and quasiparticles in semiconductors [1] to energy transfer in photosynthetic light-harvesting complexes [2] to the primary photochemical event in vision—the ultrafast isomerization of the rhodopsin protein [3]. These phenomena are typically studied using images and videos created using femtosecond laser pulses, which “freeze” ultrafast processes much like flashes of light can freeze the motion of a moving object in a series of snapshots. The quality of these photos and videos, and thus our understanding of ultrafast processes, is limited by the precision with which we can estimate the durations of femtosecond pulses and the intervals between them. Now, Vahid Ansari from Paderborn University, Germany, and co-workers have shown how time intervals between femtosecond pulses can be estimated an order of magnitude more precisely than could be achieved using previous techniques [4].
Femtosecond pulses appear and disappear too rapidly to be measured by any clock. In particular, such a short timescale precludes optical detectors involving electronics, the fastest of which respond on timescales of 1000 fs. Durations of femtosecond pulses are therefore measured using the pulses themselves through a method called optical autocorrelation. This method works by interfering a femtosecond pulse with a time-delayed copy of itself within a nonlinear crystal. Then, the resulting intensity is measured as a function of the time delay and frequency.
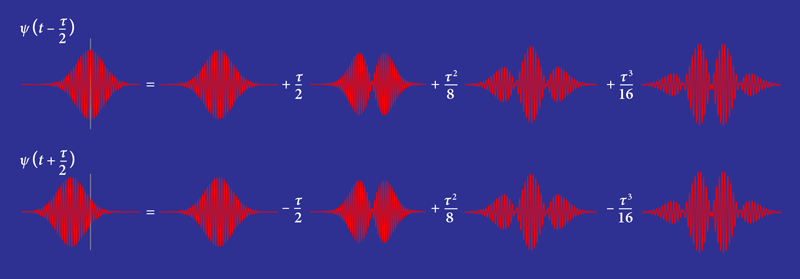
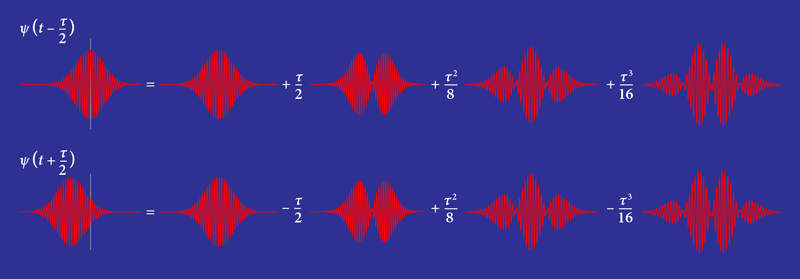
Optical autocorrelation can also be used to estimate the interval between two consecutive but overlapping femtosecond pulses. However, the method performs rather poorly. To understand the reason for this poor performance, consider two pulses separated by a time interval ( 𝜏) that is small compared to each pulse’s duration. Each pulse can be described as the sum of several temporal modes, which are the derivatives of its amplitude pulse shape (Fig. 1). While the contributions of the higher-order modes are dependent on the value of 𝜏, that of the fundamental mode is not. It is the higher-order modes, then, that carry most information about 𝜏, and it is these modes—not the fundamental mode, as in optical autocorrelation—that must be measured to estimate a small interpulse interval. Making such a measurement is what Ansari and colleagues have achieved, and they did it by building on two breakthroughs from the last decade.
The first breakthrough was a theoretical insight obtained in the context of measuring the spatial separation between two incoherent optical point sources. Using tools from so-called quantum estimation theory, researchers showed that the well-known Abbe resolution limit in such a system emerges when measurements are made on the light’s fundamental spatial mode but disappears when the higher-order spatial modes are measured instead [5]. To exploit the latter observation, they proposed a spatial mode demultiplexer (SMD) detector that would decompose the light coming from the two point sources into its component spatial modes, each of which could be measured separately with subdiffraction resolution. Ansari and co-workers “translated” this result from the spatial to the temporal domain, connecting the Abbe spatial resolution limit with the temporal resolution limit encountered when optical autocorrelation is used to measure intervals of time.
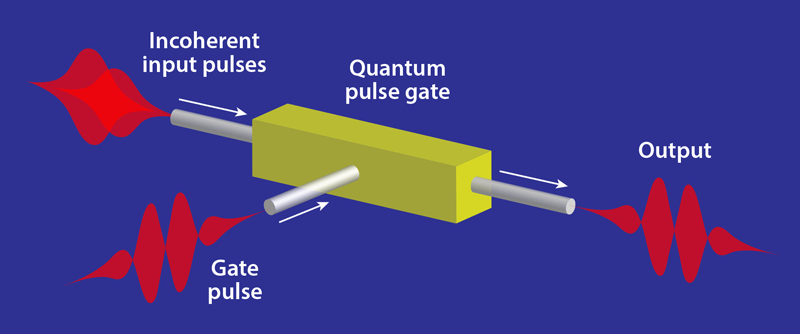
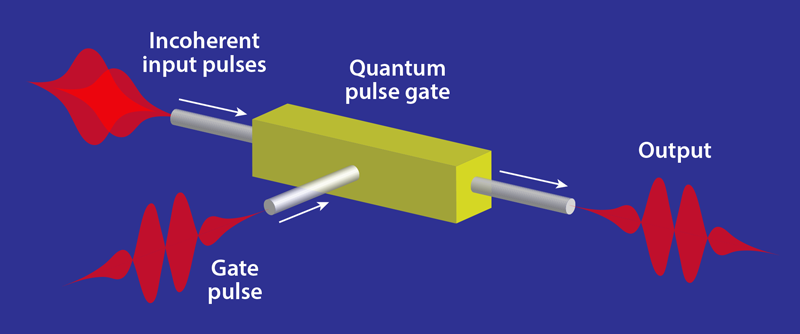
Overcoming the temporal resolution limit, however, requires the temporal equivalent of an SMD—a temporal mode demultiplexer (TMD). Enter the second breakthrough—the 2011 experimental demonstration of a TMD [6]. The scheme, called a quantum pulse gate, was developed as a tool for quantum information processing using femtosecond pulses of quantum light. The central purpose of a TMD is to allow one temporal femtosecond mode to be targeted within a multimode state of light. This targeting happens, as in an optical autocorrelator, inside a nonlinear crystal. The difference with the autocorrelator, however, is that the quantum pulse gate causes the incoming femtosecond pulse to interfere not with a time-delayed copy of itself but with a second, external pulse of light called a gate. This interference picks from the incoming pulse the specific mode that matches the gate pulse (Fig. 2).
To apply this technique to the interval-measurement problem, Ansari and co-workers constructed a quantum pulse gate in which the external gate pulses are successively set to higher-order temporal modes like those shown in Fig. 1. For each gate pulse, the output of the device changes depending on the size of the time interval ( 𝜏) between the input pulses.
Testing this approach in experiments, Ansari and colleagues measured two Gaussian pulses 1570 fs in duration, with the shortest time interval between them estimated at 30 fs. In addition to measuring the time interval, the researchers estimated the average time of arrival and the relative intensity of the pulses. Their key observation was that these quantities could be determined with a precision an order of magnitude higher than that possible using the optical autocorrelator.
The results obtained by Ansari and his colleagues may presage the application of the quantum pulse gate to a number of techniques based on resolving femtosecond timescales. Most interesting among them would be multidimensional femtosecond spectroscopy, in which the ability to resolve multiple femtosecond pulses with relative delays of a few femtoseconds can help pinpoint quantum coherences in complex molecular and solid-state systems. Experimentally, this feat will require extending the present methods down to pulse durations and interpulse intervals of a few femtoseconds [7]. Theoretically, such work will be challenging, as a TMD for estimating time intervals between multiple pulses might be significantly more complex than that demonstrated by Ansari and co-workers for just two pulses.
This temporal challenge is closely related to its spatial counterpart—finding the optimal SMD for locating multiple point sources in space, which is the focus of ongoing efforts [8]. If extended to the multipulse case, the TMD approach by Ansari and colleagues may thus provide leads on creating such an SMD, giving back to the field whose ideas it initially borrowed. This exchange would close a fruitful circular story of mutual enrichment between the fields of high-precision resolution in the space and time domains.
References
- C. L. Smallwood and S. T. Cundiff, “Multidimensional coherent spectroscopy of semiconductors,” Laser Photon. Rev. 12, 1800171 (2018).
- A. Chenu and G. D. Scholes, “Coherence in energy transfer and photosynthesis,” Annu. Rev. Phys. Chem. 66, 69 (2015).
- D. Polli et al., “Conical intersection dynamics of the primary photoisomerization event in vision,” Nature 467, 440 (2010).
- V. Ansari et al., “Achieving the ultimate quantum timing resolution,” PRX Quantum 2, 010301 (2021).
- M. Tsang et al., “Quantum theory of superresolution for two incoherent optical point sources,” Phys. Rev. X 6, 031033 (2016).
- A. Eckstein et al., “A quantum pulse gate based on spectrally engineered sum frequency generation,” Opt. Express 19, 13770 (2011).
- D. Paleček et al., “Potential pitfalls of the early-time dynamics in two-dimensional electronic spectroscopy,” J. Chem. Phys. 151, 024201 (2019).
- E. Bisketzi et al., “Quantum limits of localisation microscopy,” New J. Phys. 21, 123032 (2019).