Quantum Solution to Classical Drag Puzzle
An object moving through a fluid normally generates “drag forces,” which act to slow its motion, yet researchers still disagree about subtle aspects of the origin of such forces. New research has made a surprising connection to quantum physics, giving a unified view of how drag emerges in both ordinary fluids and quantum superfluids [1]. The improved understanding resolves some stubborn puzzles of classical fluid physics and may inspire new techniques for reducing drag in practical fluid flows.
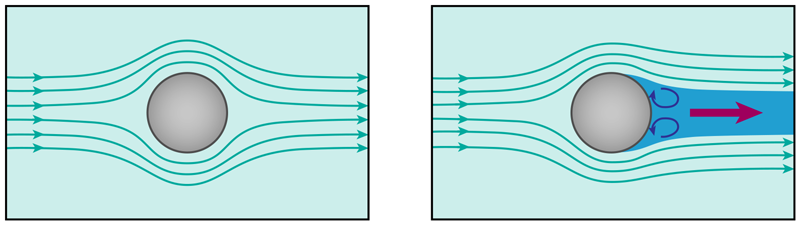
In the mid 18th century, French mathematician Jean-Baptiste le Rond d’Alembert first applied Newtonian physics to the motion of fluids, considering how, for example, a fluid should move past a rigid sphere or similar object. He assumed that the fluid smoothly diverts around the object, forming a stable flow characterized by largely undisturbed streamlines. For ideal fluids lacking viscosity, he showed that the equations implied no force at all acting on the object, in clear contradiction to experience. An object immersed in a stream of water or air undeniably gets pushed along with the flow.
Physicists later resolved this apparent paradox by showing that the nonzero viscosity of real fluids produces drag forces through a variety of mechanisms, including the formation of semi-attached, slow-moving boundary layers near an object’s surface. As Gregory Eyink of the Johns Hopkins University, Maryland, points out, however, this work didn’t completely resolve d’Alembert’s puzzle. The influence of viscosity dwindles as fluids flow more rapidly, so it seems that very fast flows really should behave as d’Alembert showed, producing zero drag. Yet many careful experiments clearly demonstrate that this isn’t true.
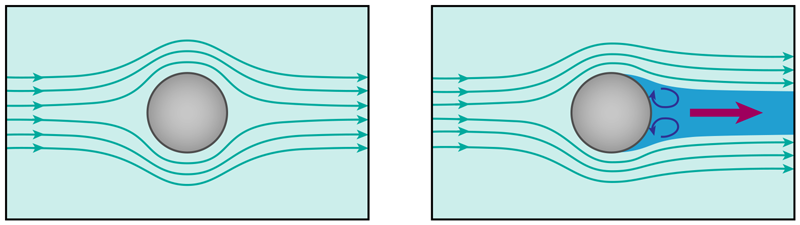
This longstanding paradox, Eyink now argues, can be resolved by taking inspiration from quantum physics. Unlike any classical fluid, quantum superfluids—such as ultracold liquid helium-4—truly have zero viscosity. When the speed is low enough, an object can move through such a fluid with no drag at all. (The fluid is able—counterintuitively—to exert the same pressure on the front and back of the object.) But drag does arise abruptly when the object reaches a critical speed, at which point quantized vortices—localized swirls—form near the surface of the object and move perpendicular to the main flow. The vortices’ motion generates a drop in pressure, creating an effective drag on the object. An equation known as the Josephson-Anderson relation captures this effect in superfluid flows.
Starting from the fundamental equations for classical fluids, Eyink has now derived an analogous relation, showing that essentially the same mechanism also produces drag in classical fluids. Eyink got the idea while studying a previously derived result extending the Josephson-Anderson relation to flow through a channel [2]. He decided to apply the same formalism to flow around a body. “Once I sat down and tried, I worked out the main steps in a single weekend,” Eyink says.
The new relation describes how the flow of fluid past any rigid object, even in the absence of viscosity, stirs up vortices and swirling flows in the fluid, which then move across the prevailing flow. This motion is the origin of drag, according to Eyink. “Even though vorticity, or swirling motion, isn’t quantized in water and air, drag is due to motion of vorticity across the flow,” Eyink says. The effect solves the old puzzle, as the vorticity doesn’t disappear at high speeds.
“I find the analysis very thought-provoking,” says fluid dynamicist Marc Brachet of the École Normale Supérieure in Paris. “This new Josephson-Anderson relation generalizes earlier theories and also allows for a qualitatively and quantitatively new understanding of drag.”
Eyink suggests that it should be possible to explore the consequences of his new relation, as the vorticity within a flow can be measured accurately in modern experiments or calculated precisely in numerical simulations. Such studies might offer insights into drag-reducing strategies that involve adding polymers to a fluid. These polymer mixtures are widely used to increase flow through porous rocks in mining operations and through hoses used by firefighters, but why they work is still somewhat of a mystery. Eyink speculates that the polymers may slow down the vorticity flow from walls—an effect that could be observed in flow measurements.
–Mark Buchanan
Mark Buchanan is a freelance science writer who splits his time between Abergavenny, UK, and Notre Dame de Courson, France.
References
- G. L. Eyink, “Josephson-Anderson relation and the classical d'Alembert paradox,” Phys. Rev. X 11, 031054 (2021).
- E. R. Huggins, “Energy-dissipation theorem and detailed Josephson equation for ideal incompressible fluids,” Phys. Rev. A 1, 332 (1970).