Turning a Quantum Computer into a Time Crystal
Today’s quantum computers are far from ideal—they have only a few dozen quantum bits, and these “qubits” are noisy, prone to random errors that can’t be corrected. However, a team of researchers has now shown that such “noisy intermediate-scale quantum” (NISQ) devices can nevertheless be used to simulate a complex type of quantum behavior. They show theoretically that an NISQ device like Google’s Sycamore quantum computer can be used to simulate an object called a discrete time crystal, whose components undergo spontaneous collective oscillations [1]. In a separate paper the researchers collaborate with the Google team to put their approach into practice on Sycamore [2]. Another team has also recently reported a similar quantum simulation enacted using qubits of a different type [3].
Time crystals, first proposed in 2012 [4], are systems that periodically return to a specific configuration—they are crystals that repeat in time rather than in space. For example, some systems made of many interacting quantum components are predicted to act as time crystals when driven by a periodically varying force. A classical pendulum also oscillates in response to a periodic driving force, but a periodically driven time crystal resonates at an integer multiple of the drive’s period (a lower frequency than that of the driving force). Such a system is called a discrete time crystal (DTC).
However, making a true DTC that oscillates indefinitely is challenging because the driving force injects energy into the system and causes it to heat up, which eventually overwhelms the periodic dynamics. Certain quantum systems that contain disorder can, in theory, avoid such heating through a mechanism called many-body localization (MBL), which prevents energy from spreading through the whole system and thus stabilizes a DTC. But although DTC-like oscillations have been reported previously in quantum experiments [5–7], no one has been able to use MBL (or any other method) to stabilize a DTC and allow it to oscillate indefinitely.
Quantum computers provide a unique opportunity for making a time crystal because they are precisely controllable quantum systems. In principle, any quantum object that can change its state can form a quantum DTC, so when implementing one on a quantum computer, the boundary between simulation and real experiment is blurred. “[It] is best viewed as an experiment on a many-body system, rather than the output of an imperfect [noisy] computer simulation,” says Matteo Ippoliti of Stanford University.
He and his co-workers have now shown that an indefinitely stable DTC can be simulated on Google’s Sycamore quantum processor, which uses superconducting devices as its qubits. The Stanford team writes that their algorithm for realizing a DTC on Sycamore can deliver genuine MBL, so that, in theory, the periodic behavior can be sustained indefinitely. “We lay out a blueprint for the first realization and detection of an MBL DTC, and the Sycamore circuit indeed meets all the desired conditions,” says Ippoliti. In their scheme, the qubits work as a chain of interacting spins that can point “up” or “down.” By controlling their orientation with a periodically varying force, the spins can be made to flip back and forth along the chain at a lower frequency than that of the driving force.
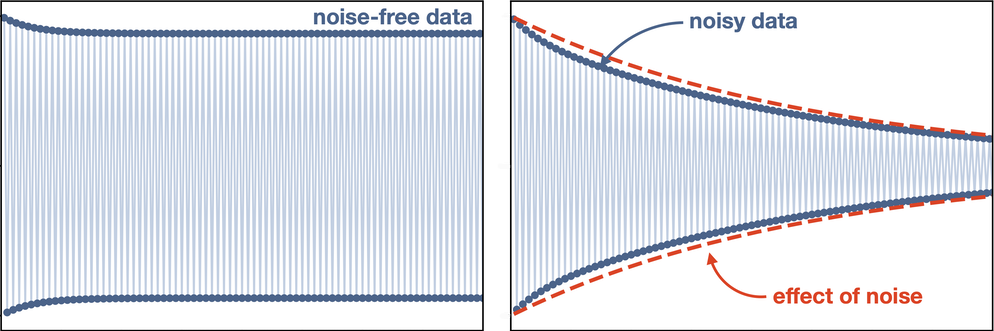
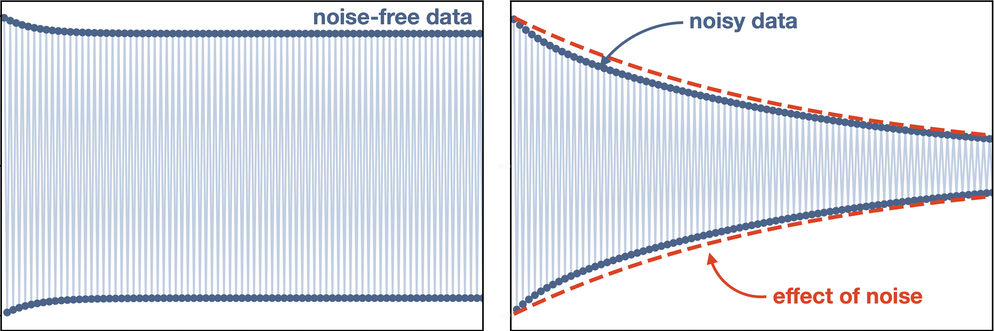
The key MBL DTC signature, the researchers say, is that an oscillatory signal with a period that is some multiple of that of the driving force will emerge from any initial state of the system—a feature that can’t easily be checked in other experiments but is straightforward to investigate using this quantum-computational algorithm.
In collaboration with Google researchers, the team has also shown that their scheme works in practice, using 20 of the 53 qubits in the Sycamore circuit [2]. However, in those experimental runs, the DTC behavior could only be watched for less than a millisecond (about a hundred oscillations). That’s because, as with any quantum computation, the qubits can only be kept in the quantum-coherent state needed for the computation for a short time before interactions with their environment induce decoherence that breaks the simulation. Nevertheless, the strategy outlined by Ippoliti and colleagues describes how to distinguish the fingerprint of true (in principle, indefinitely sustained) DTC behavior from dynamics that might mimic it for short times, as seen in previous experiments. That approach—which the team used in their analysis of the Sycamore data—involves looking at the detailed statistics of fluctuations in the oscillation amplitudes.
The researchers stress that this DTC behavior can also, in principle, be simulated on a classical computer. But in that case, “the bits in the computer evolve in a way that looks nothing like the physics we're interested in but nevertheless output numbers that replicate the outcomes of a hypothetical experiment,” Ippoliti says. In contrast, on a quantum computer, the qubits themselves exhibit the DTC behavior.
“Our work shows the great potential of NISQ devices for exploring nonequilibrium phases of matter,” says Ippoliti. Quantum physicist John Preskill of the California Institute of Technology concurs. “The authors argue persuasively that previous experiments seeking evidence for a DTC phase actually found a transient state instead and that the Sycamore platform provides tools for a more convincing demonstration,” he says. What’s more, Preskill thinks that NISQ devices might be able to probe such periodically driven quantum systems in regimes that classical algorithms can’t easily simulate.
Norman Yao of the University of California at Berkeley says that “it’s a cool result.” He was part of the team, led by researchers at the Delft University of Technology in the Netherlands, that recently also showed sustained MBL DTC behavior in a quantum simulation [3]. In that case, the nine qubits used were carbon nuclear spins in a diamond crystal, and the time crystal oscillated for about 800 cycles. However, direct comparison with the Stanford team’s work is complicated because there are many differences between the two experiments.
–Philip Ball
Philip Ball is a freelance science writer in London. His latest book is How Life Works (Picador, 2024).
References
- M. Ippoliti et al., “Many-body physics in the NISQ era: Quantum programming a discrete time crystal,” PRX Quantum 2, 030346 (2021).
- X. Mi et al., “Observation of time-crystalline Eigenstate order on a quantum processor,” arXiv:2107.13571.
- J. Randall et al., “Observation of a many-body-localized discrete time crystal with a programmable spin-based quantum simulator,” arXiv:2107.00736.
- F. Wilczek, “Quantum Time Crystals,” Phys. Rev. Lett. 109, 160401 (2012).
- S. Choi et al., “Observation of discrete time-crystalline order in a disordered dipolar many-body system,” Nature 543, 221 (2017).
- J. Zhang et al., “Observation of a discrete time crystal,” Nature 543, 217 (2017).
- J. Rovny et al., “Observation of discrete-time-crystal signatures in an ordered dipolar many-body system,” Phys. Rev. Lett. 120, 180603 (2018).