Excitations in the Ultimate Quantum Fluid
At low temperatures, helium is the ultimate quantum fluid, or “superfluid,” exhibiting behaviors that are dominated by quantum-mechanical fluctuations. These fluctuations give rise to a menagerie of effects that can be both entertaining (a cup of liquid helium can empty itself) and potentially problematic (“superleaks” can compromise low-temperature experiments). Understanding and predicting such behaviors has been an active line of research since they were first observed in the 1930s [1, 2]. Now, Henri Godfin at Grenoble Alpes University, France, and colleagues have carried out a new study of superfluid helium’s excitations that provides important constraints that could support or rule out certain theoretical models of superfluidity [3]. The result is an experimental tour de force, establishing the superfluid dispersion relation to an unprecedented precision.
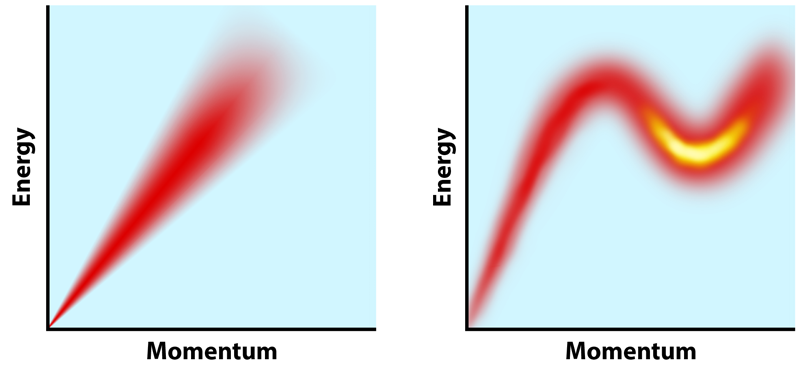
A material’s dispersion relation describes how the material responds to a perturbation. For example, when a sound wave (or phonon) travels in a material, the dispersion relation defines the relationship between the energy and the momentum of the phonon. For small momenta this relationship is linear, and the slope of the line gives the speed of sound in the material. In a conventional fluid, sound waves are strongly damped, and this linear regime therefore represents the complete dispersion spectrum: at higher perturbation energies the phonons cannot be kept coherent and the excitation dies out.
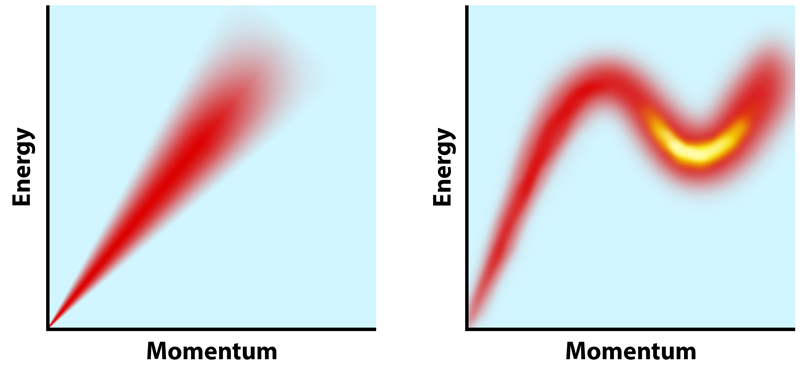
In superfluid helium the dispersion relation is more complicated: the excitation spectrum shows an unusual dip before disappearing (Fig. 1). Although the detailed origin of this dip is still debated, its source is likely the same one that causes the peculiar superfluid behaviors that amuse and confound experimentalists: helium-4, which makes up more than 99% of helium atoms, is a boson, consisting of two protons and two neutrons. In a bosonic fluid, multiple particles can occupy a given quantum state. When liquid helium is cooled below its superfluid transition temperature (2.2 K), a significant fraction of the helium-4 atoms condense into the same lowest-energy quantum state, producing a macroscopic quantum state in which all participating particles travel together.
The result of this coherence is a fluid with zero viscosity, which can sustain excitations beyond the simple longitudinal phonons seen in a normal fluid. Within the anomalous low-energy dip in the dispersion relation, these excitations are called rotons. Like phonons, rotons are the quantized manifestations of sound waves. But whereas phonons oscillate only longitudinally, rotons are more complex, carrying some vorticity—in one model, they resemble a smoke ring. Many scientists have considered the problem of the roton minimum in the dispersion, beginning with Lev Landau [4], who earned the 1962 Nobel Prize for his theory connecting it to sound waves. Despite the attention this problem has received, our understanding of the spectral feature is still incomplete. One reason for this knowledge gap is that superfluid helium’s dispersion relation has been, until now, only partially characterized.
Neutron scattering has been the main technique for measuring dispersion relations, although other methods—in particular those that measure the propagation of ultrasound pulses—have contributed to characterizing limited parts of the spectrum. These experiments have established qualitative features of the spectrum, but the various data do not always match [5]. Godfrin and his colleagues have now made sense of these earlier studies with careful inelastic-neutron-scattering measurements of the excitation spectrum over the full range of energies and momenta. They performed these measurements at various temperatures and at pressures up to 24 bars.
This wide span of parameters allowed them to explore the superfluid’s properties comprehensively, including changes in behavior close to the superfluid’s freezing point. Importantly, the researchers outlined in detail the methods they used to test the data, which should aid future investigations into similar systems. By considering all potential sources of error—in their own as well as in previous experiments—they explained discrepancies between different measurement techniques and benchmarked their work against earlier studies. The result is the most complete and precisely measured dispersion relation for superfluid helium to date.
As a material’s excitations govern its thermodynamic characteristics, knowing the full dispersion relation allows the calculation of properties such as heat capacity and particle density. Prior to the new measurements, such calculations were based on an accepted parametrization derived from conflicting data sets. With more reliable information about the dispersion relation as a function of temperature and pressure, these properties can now be determined with greater confidence. Godfrin and his colleagues have already made progress in this respect, finding good agreement between the empirically derived value for superfluid helium’s heat capacity and the value calculated analytically and numerically from their measured dispersion relation.
Pushing the experimental precision for a specific problem has often resulted in dramatic progress in other areas, as it improves researchers’ ability to vet fundamental models. As the simplest bosonic fluid, superfluid helium offers an ideal system that could help in developing theories for rotons. Models that are favored by new data can be applied to other systems that support roton-like excitations, which include ultracold bosonic gases in which the dimensionality is strongly constrained. The study by Godfrin and colleagues provides a clear benchmark for such winnowing of theories, which I anticipate will significantly further our understanding.
References
- P. Kapitza, “Viscosity of liquid helium below the 𝜆-point,” Nature 141, 74 (1938).
- J. F. Allen and A. D. Misener, “Flow of liquid helium II,” Nature 141, 75 (1938).
- H. Godfrin et al., “Dispersion relation of Landau elementary excitations and thermodynamic properties of superfluid 4He,” Phys. Rev. B 103, 104516 (2021).
- L. Landau, “The theory of superfluidity of helium II,” J. Phys. U.S.S.R. 5, 71 (1941); “On the theory of superfluidity of helium II,” J. Phys. U.S.S.R. 11, 91 (1947).
- H. R. Glyde, “Excitations in the quantum liquid 4He: A review,” Rep. Prog. Phys. 81, 014501 (2017).