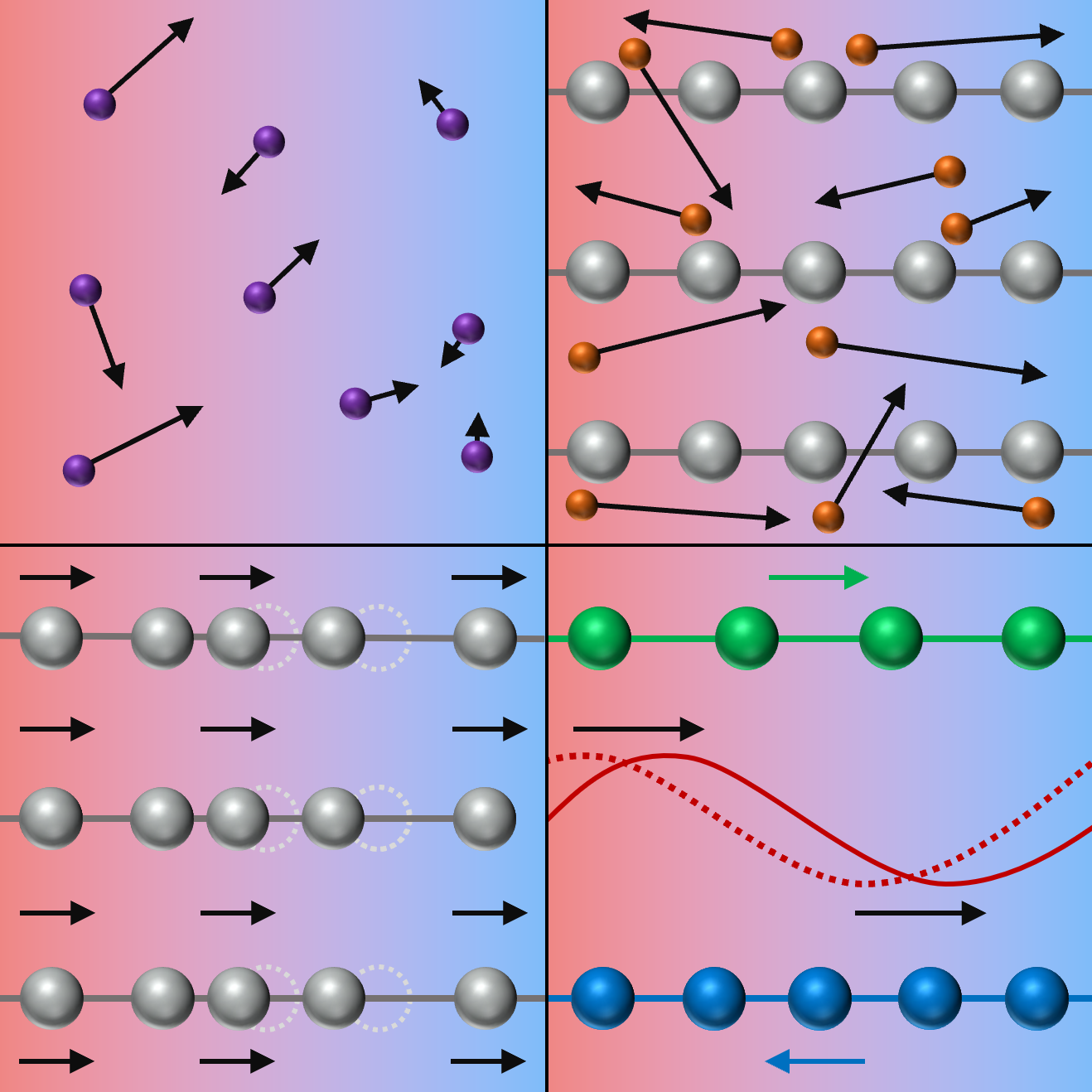
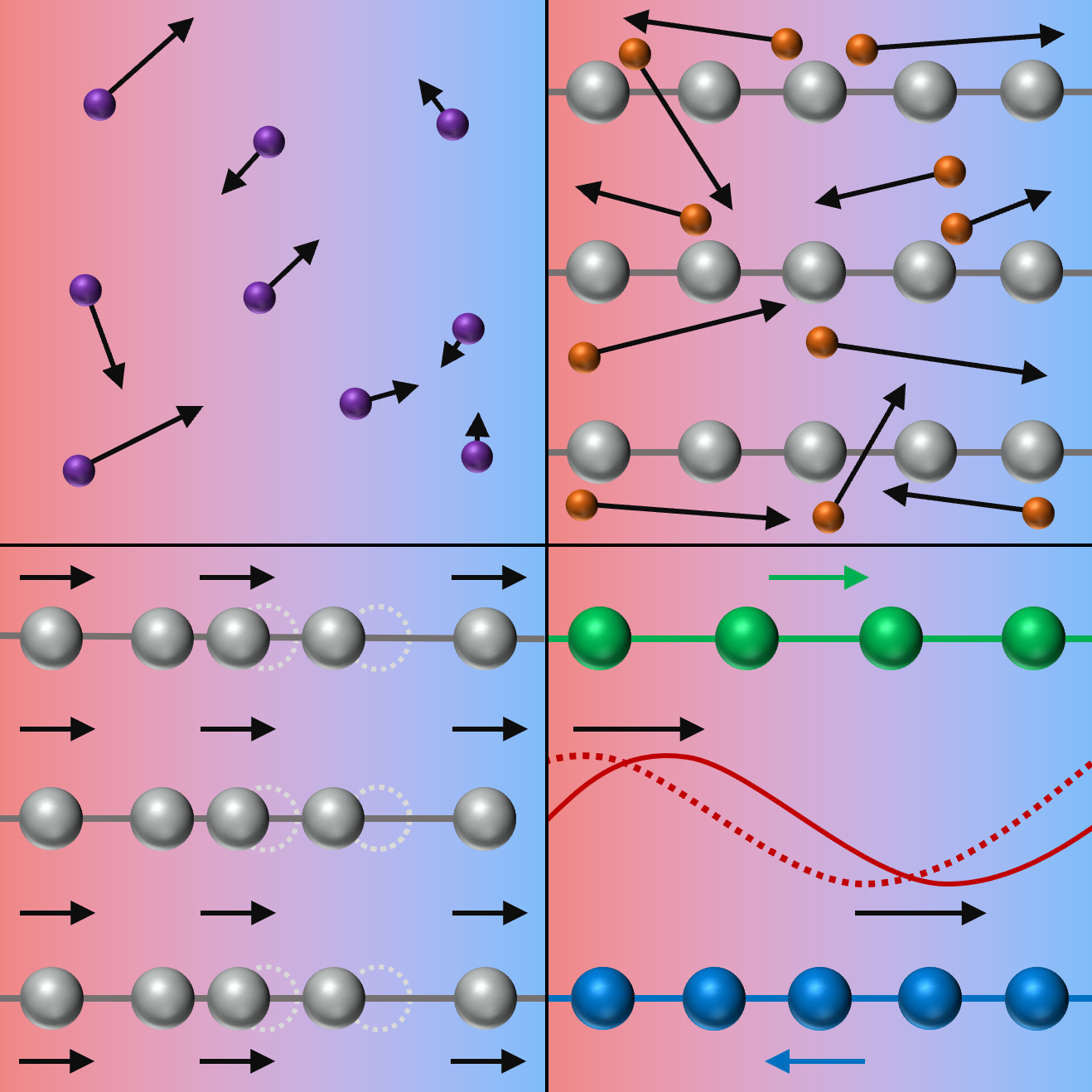
Cooking with Phason Gas

Evan Constable

Viewpoint

Cooking with Phason Gas

Institute for Solid-State Physics, Vienna University of Technology, Vienna, Austria

December 14, 2022• Physics 15, 193

Heat-transport measurements and neutron-scattering spectroscopy probe a form of thermal conduction based on excitations called phasons.

Figure caption — **Figure 1:** Four ways in which heat can be transferred across a temperature gradient. The number, direction, and length of the black arrows reflect the density, propagation direction, and speed of the heat carriers, respectively. In an ideal gas (top left), thermal transport occurs when particles (purple) diffuse from the hot side to the cool side. In an electron gas (top right), the heat carriers are electrons (orange) within an atomic lattice (gray). In a phonon gas (bottom left), heat transfer occurs through phonons (lattice vibrations). Finally, in a phason gas (bottom right), heat is transported by excitations called phasons. A phason (red) is produced by the relative shift of two sublattices (green and blue) with periodicities whose ratio is an irrational number.

The understanding of how substances conduct heat is of great significance in materials science. It is needed for many important technological applications—from heat management in electronics to temperature control in buildings [1]. Therefore, when an unusual form of thermal transport is identified, materials scientists take notice. Michael Manley of Oak Ridge National Laboratory, Tennessee, and his colleagues have shown that excitations called phasons can provide the main contribution to thermal transport in a material known as fresnoite [2]. Phasons are collective lattice oscillations that occur in certain crystals with an aperiodic lattice structure—fresnoite being one of the best known. The researchers’ demonstration could pave the way for new heat-management strategies.

Thermal conductivity is a measure of a material’s ability to transfer heat. It is a property that we are all abruptly reminded of when we accidentally place our hand on a hot kitchen stove. The temperature gradient between our cooler skin and the hotter surface facilitates a transfer of energy into our hand, resulting in an unpleasant sensation. The notion that different materials conduct heat at different rates is similarly experienced when we perceive the cooling sensation of holding a metal spoon relative to a wooden one.

At the microscopic level, thermal conduction is a kinetic process. Just as electrical conduction describes the transport of charge by particles, thermal conduction similarly describes the transport of energy by particles. In an ideal gas, for example, fast-moving particles on the hotter side of a temperature gradient diffuse and collide with slow-moving particles on the cooler side [3] (Fig. 1, top left). Thermal conductivity quantifies how quickly energy is transferred across the gradient. Its value is proportional to the heat capacity of the gas (related to the density of particles), the average particle speed (effectively, the speed of sound in the gas), and the particle mean free path (how far each particle travels on average before colliding with another particle).

A metal, defined by its internal “gas” of freely moving electrons, conducts heat in a similar way to an ideal gas (Fig. 1, top right). In this case, the kinetic particles are electrons that exist in a much higher density than the particles in a typical molecular gas. These electrons have a high speed (about 10⁶ m/s) and a mean free path approaching that of a diffuse gas (roughly 10–100 nm). Thus, for the same reason that metals are good electrical conductors, they are also excellent thermal conductors.

In an electrical insulator, heat must travel via a different pathway—typically, through atomic-lattice vibrations called phonons (Fig. 1, bottom left). At the quantum level, phonons behave as individual particles, and at ambient temperature, they can exist in a high density. However, this high density also means that they frequently scatter off one other, and with speeds limited to the speed of sound in the material (about 10³ m/s), they have a small mean free path (smaller than 10 nm). Therefore, compared with metals, electrical insulators are generally poor thermal conductors.

Whereas phonons represent shifts in the atomic positions of a single lattice, phasons represent shifts in the relative position (phase) of two or more sublattices consisting of many atoms (Fig. 1, bottom right). Phasons emerge only in incommensurate materials—aperiodic crystals that contain multiple sublattices with periodicities whose ratio is an irrational number, such as in fresnoite [4]. Many atoms can contribute to phasons, so the density of phasons is lower than the density of phonons. However, as Manley and colleagues previously demonstrated in fresnoite, phasons can be much faster than phonons because of the nonlinear way in which they interact with the underlying lattice [5].

The possibility that phasons could provide a significant contribution to the thermal conductivity of incommensurate materials had been previously considered [6]. Heat-transport measurements and sophisticated modeling supported the idea, but these approaches alone were not definitive. What remained unknown was whether the mean free path of phasons could be large enough for their contribution to be relevant compared with the phonon contribution.

Manley and colleagues addressed this uncertainty by conducting complementary heat-transport measurements and neutron-scattering spectroscopy of fresnoite. They determined that the speed and mean free path of phasons in fresnoite are, on average, about 3 times higher than the values for phonons. Consequently, the phason contribution to the thermal conductivity is at least 2.5 times that of the phonon contribution.

A direct impact of this work concerns thermoelectric materials—those that can convert waste heat into useful electricity. These materials require a rare combination of high electrical conductivity and low thermal conductivity. Incommensurate metals have been proposed as promising thermoelectric candidates because they are good electrical conductors and poor phonon conductors [7]. However, Manley and colleagues’ results suggest that poor phonon conductivity does not necessarily imply low thermal conductivity because of the significant phason contribution.

Phason-based heat transport in incommensurate materials is not going to rival electron-based transport in metals any time soon. However, harnessing the transport properties of phasons could open paths to efficient thermal-management materials and even to thermal logic circuits—digital circuits based on thermal transport instead of electron transport. Such devices, when integrated with conventional electronic circuits, could collect energy usually lost to heat dissipation and put it back to work in computational processes, greatly improving the efficiency of computing devices [8].

References

M. Beekman and D. G. Cahill, “Inorganic crystals with glass-like and ultralow thermal conductivities,” Cryst. Res. Technol. 52, 1700114 (2017).
M. E. Manley et al., “Phason-dominated thermal transport in fresnoite,” Phys. Rev. Lett. 129, 255901 (2022).
C. Kittel and H. Kroemer, Thermal Physics (W. H. Freeman, New York, 1980)[Amazon][WorldCat].
R. Zeyher and W. Finger, “Phason dynamics of incommensurate crystals,” Phys. Rev. Lett. 49, 1833 (1982).
M. E. Manley et al., “Supersonic propagation of lattice energy by phasons in fresnoite,” Nat. Commun. 9, 1823 (2018).
A. Smontara et al., “Contribution of charge-density-wave phase excitations to thermal conductivity below the Peierls transition,” Phys. Rev. B 48, 4329 (1993).
N. Sato et al., “Glass-like lattice thermal conductivity and thermoelectric properties of incommensurate chimney-ladder compound ${FeGe}_{𝛾}$ ,” Chem. Mater. 28, 529 (2016).
N. Li et al., “Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond,” Rev. Mod. Phys. 84, 1045 (2012).

About the Author

Evan Constable is a senior postdoctoral researcher in the solid-state-spectroscopy group at Vienna University of Technology. He received his PhD in physics from the University of Wollongong in Australia, where his research focused on terahertz spectroscopy of magnetic systems. He previously worked at the Néel Institute in France, where he combined optical and neutron-scattering techniques to study frustrated magnetic systems. He is currently the principal investigator on the EMERGE project, which seeks to probe the emergent electrodynamics of frustrated magnets. His other research topics include terahertz optics, magnetoelectrics, antiferroelectrics, thermoelectrics, and charge-ordered systems.