Optical Fibers Go Topological
Using concepts from the mathematical field of topology, researchers at the University of Bath, UK, have designed an optical fiber that can robustly propagate light, even if there are variations in the properties of its light-guiding materials or in its overall geometry [1]. The team thinks that this newfound topological protection could enable advances in optical communication and photonic quantum computing.
The concept of topology is often explained using a joke about a donut and a coffee cup. A coffee cup made of rubber can be continuously twisted and stretched—no cuts need to be made—so that it takes on the shape of a donut. Even though the object’s outline changes under this transformation, its essence remains the same—it contains one hole. Thus, the quip goes, a topologist cannot tell the difference between the two things.
More explicitly, topology is concerned with the global properties of a system that remain constant when some parameter of the system is continuously changed: for the coffee cup and the donut, the constant property is the number of holes and the changing parameter is the 3D geometry. Quantum systems can also sit in topological states, which retain some global property, even when local perturbations, such as experimental noise, are introduced. That stability can allow these states to survive longer than their nontopological counterparts, making them attractive for use in quantum computing.
For their study, Nathan Roberts and his University of Bath colleagues started with one of the simplest topological models: the Su–Schrieffer–Heeger (SSH) model. In the SSH model, electrons hop along a 1D lattice. The coupling strength of neighboring lattice sites determines how easily the electrons hop and alternates between a high (easy) and low (difficult) value. The model predicts that the two ends of the chain can develop topological states, in which the electrons are confined to these edge sites. These states are highly localized and are robust against small changes in the coupling strengths between sites. That the SSH model is simple to implement and exhibits these localized, topological states made it an attractive starting point for building topologically protected fibers.
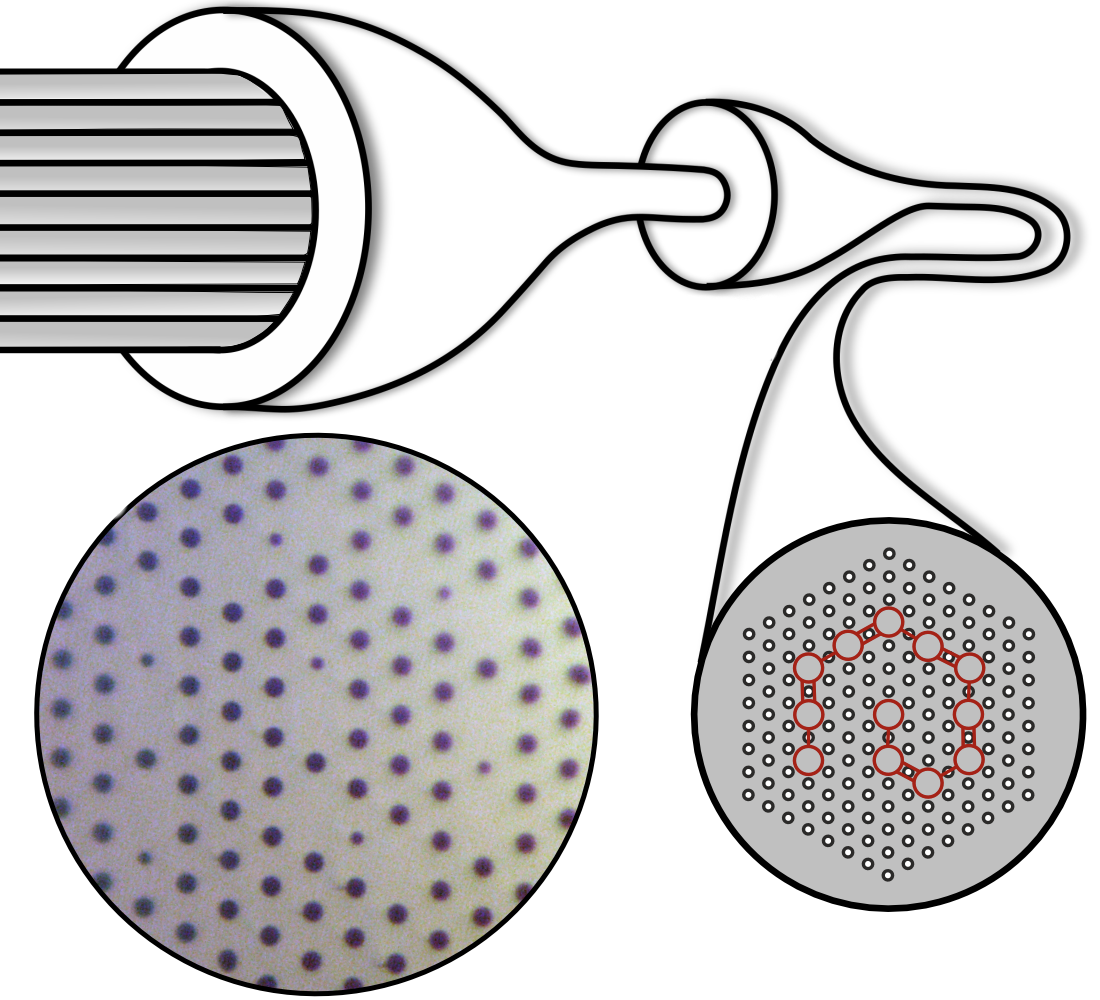
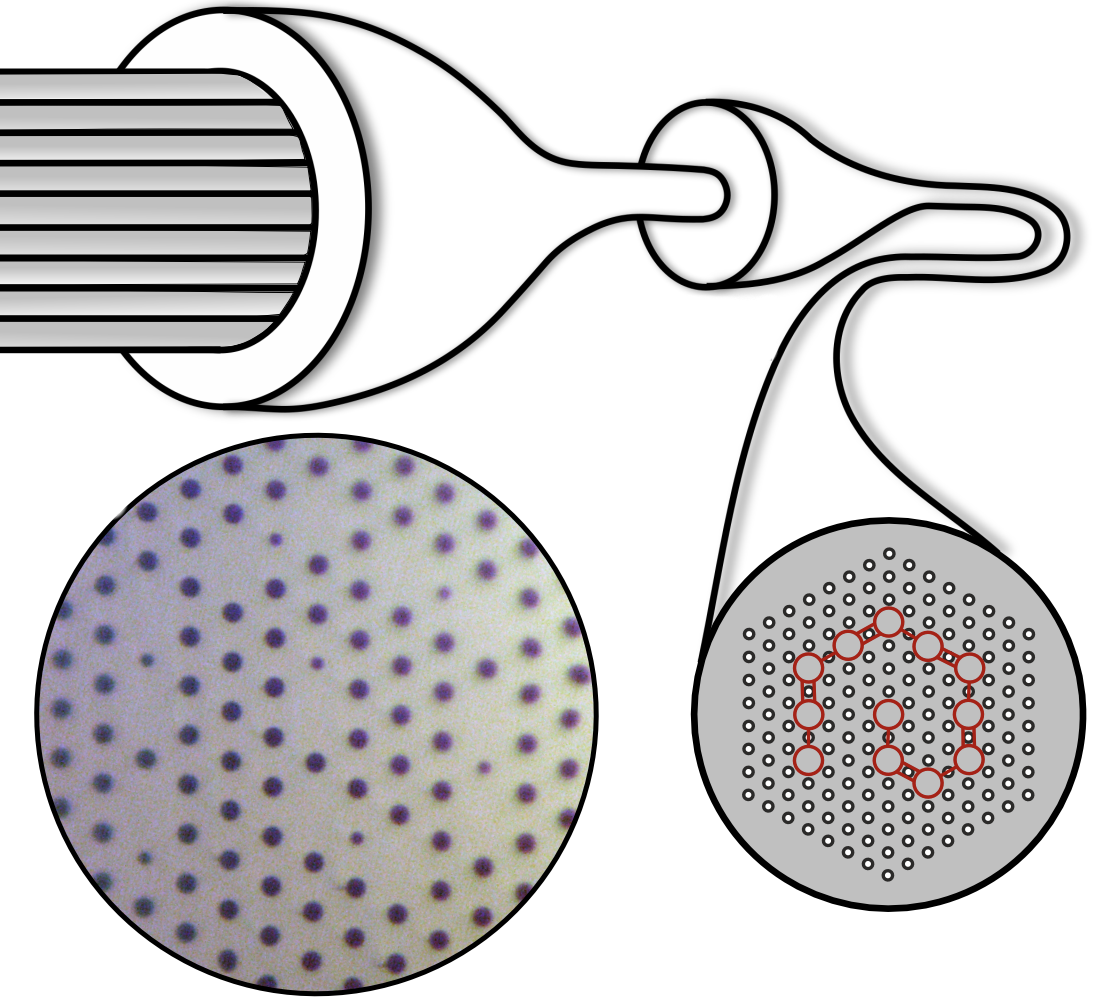
To implement the model in an optical fiber, the researchers replaced the electrons with photons and the lattice sites with solid-core rods through which light could propagate. To make the fiber, they stacked hollow glass tubes and the rods in a hexagonal pattern. The rods spiraled outward from the center of the stack and the tubes encased the whole structure. The complete assembly was then stretched like taffy and drawn into a thin 160- 𝜇m-diameter fiber.
The periodic pattern of holes created from the encasing tubes formed the fiber’s outer “cladding”—a region through which light cannot propagate—while each of the 12 rods formed a separate channel through which light could travel, the equivalent of an SSH site. The team adjusted the air gaps between the 12 cores so that they alternated between short and long, giving them high and low coupling between neighboring cores and a 1D SHH chain. The researchers then shone light down each core and observed how it propagated.
The team found that when light was shone down a core in the middle of the SSH chain, the light quickly spread out, populating neighboring cores. But when light was shone down either of the rods at the ends of the spiral, the light stayed confined in that core as it traveled along the length of the fiber.
To test whether these “edge” states were topological, as the SSH model predicts, Roberts and his colleagues looked at how the fiber transported light when there were imperfections in its properties, which they induced by gently bending the fiber. Like a race car speeding around a circular track, light traveling around the outside of a bent fiber must travel farther than light traveling around the inside. Such position-dependent disorder can be a problem for maintaining light coherence along a fiber. But this disorder wasn’t as much of a problem for the system when the team exploited one of the fiber’s topological states.
Andrea Alù, a theoretical physicist at City University of New York, finds this new experiment exciting. “While the theoretical framework is somewhat established, the application [of topology] to optical fibers is interesting and makes the guided mode more robust and resilient to certain types of defects,” he says.
Roberts and his colleagues now plan to build on this work by designing other optical fibers with topological states. They also plan to expand from 1D to 2D. Team member Peter Mosley says, “With 2D designs we’re more likely to find [applications] that are actually of some possible practical use.”
–Katie McCormick
Katie McCormick is a freelance science writer based in Sacramento, California.
References
- N. Roberts et al., “Topological supermodes in photonic crystal fiber,” Sci. Adv. 8 (2022).