Fractional Jumps in Quantum Hall Interferometer

Steven H. Simon

Viewpoint

Fractional Jumps in Quantum Hall Interferometer

Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford, UK

October 23, 2023• Physics 16, 183

A new experiment with fractional quantum Hall states provides further evidence that the states’ characteristic quasiparticles obey fractional statistics.

Figure caption — **Figure 1:** The quantum Hall interferometer consists of a two-dimensional material (blue) with a cavity structure (yellow) in its center. When a magnetic field and a voltage are turned on, currents (red lines) flow along the edge of the material. Reflections at the entrances of the cavity lead to interference effects in the measured conductance. For certain field and voltage values, the interference pattern exhibits phase jumps because of the changes in the number of quasiparticles (orange) inside the cavity.

Particles such as electrons and photons belong to one of two camps, fermions or bosons, that differ in their statistical behavior. However, in 1977, Jon Magne Leinaas and Jan Myrheim postulated that particles confined to two dimensions can have “fractional” statistics lying between those of fermions and bosons [1]. Now an experiment by James Nakamura and colleagues from Purdue University in Indiana offers a direct measure of fractional statistics in a system long predicted to harbor them: a thin strip of semiconductor exhibiting the fractional quantum Hall effect (FQHE) [2]. Previous work by the same authors saw evidence of this predicted behavior, but the new experiment probes an FQHE state whose statistics are more unambiguously fractional. The signal is still not as clear as one might like, but the odds are that further experimental refinements will give undeniable confirmation of statistics beyond those of fermions and bosons.

The notion of fractional statistics can be understood by imagining the swapping of two identical particles in a counterclockwise direction on a two-dimensional (2D) surface. At the end of such an exchange, the wave function accumulates a phase $e^{i 𝜃}$ , where $𝜃$ defines the exchange statistics. For bosons $𝜃 = 0$ , whereas for fermions $𝜃 = 𝜋$ . But other values of $𝜃$ are also possible, in which case we say that the statistics are fractional. One place to look for fractional statistics is in FQHE—a quantized conductance in 2D materials exposed to a magnetic field. Soon after the discovery of FQHE in 1986, theorists predicted that the quasiparticle excitations of FQHE states should have both fractional charge and fractional statistics [3]. While the fractional charge of these exotic particles was measured long ago (first in the 1990’s [4], and many times since), the measurement of the fractional statistics has proved more elusive.

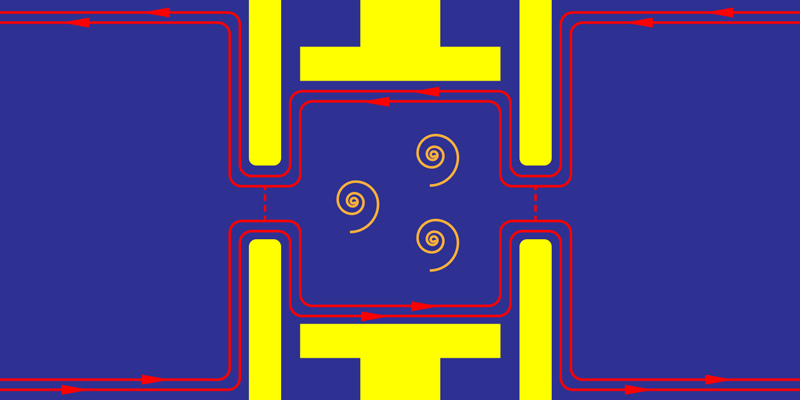
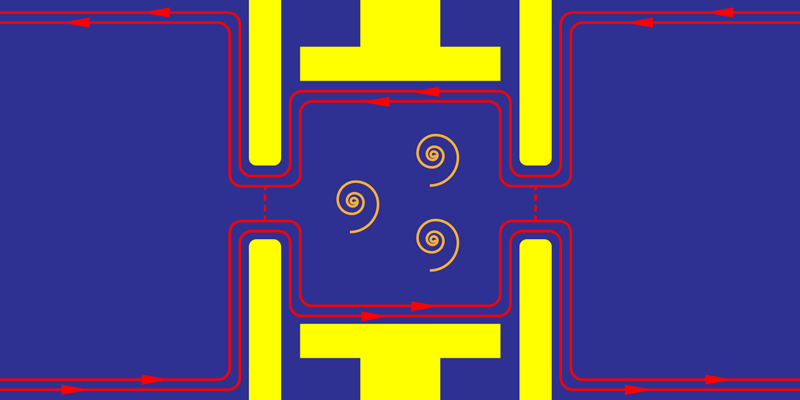
Just in the past few years, several new experiments have been performed that have finally given fairly clear evidence of fractional statistics [5–9]. The most direct, and potentially the most conclusive, is the set of experiments by Nakamura and colleagues [5, 6]. These experiments use a Fabry-Pérot edge-state interferometer—a setup based on an earlier proposal [10]. In this experiment, two constrictions are added to the surface of a 2D material in an FQHE state. These constrictions, or “point contacts,” act like partially reflecting mirrors for the FQHE edge modes, which one can think of as currents of quasiparticles moving around the border of the 2D material. Together, the two point contacts form a cavity. When, for example, a right-moving edge mode approaches this cavity, it is split into two partial waves. One partial wave is immediately reflected back to the left. The other partial wave encircles the cavity and then interferes with the first partial wave (Fig. 1). The researchers measure the conductance through the device as the parameters of the experiment (gate voltage and magnetic field) are varied, and they observe an oscillation between constructive and destructive interference.

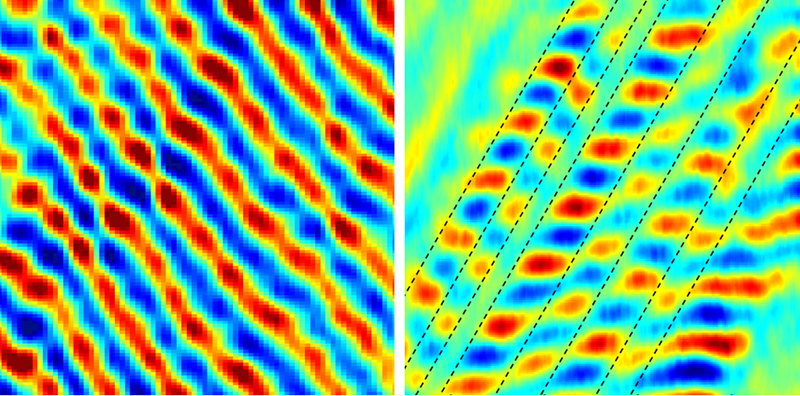
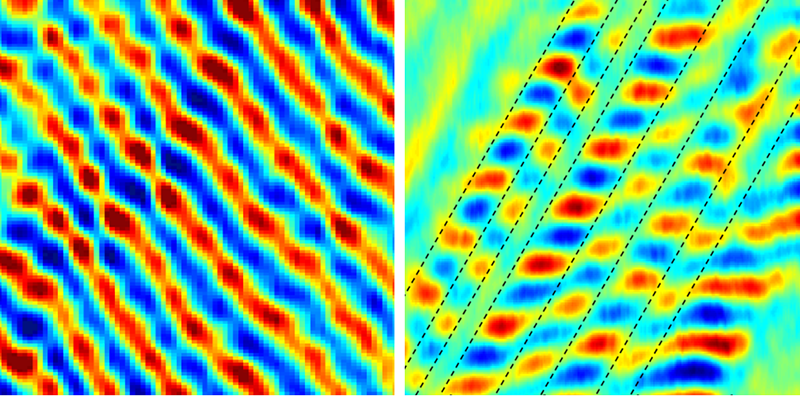
The interference oscillations are simply a wave effect, but there is a signature of fractional statistics within the oscillations. In a certain region of parameter space, small changes of the magnetic field or gate voltage can induce the appearance of one extra quasiparticle in the middle of the cavity. The added quasiparticle causes the mode running around the cavity to accumulate an additional phase of $e^{2 i 𝜃}$ (corresponding to two counterclockwise exchanges), which is then measured as a sudden change, or discrete phase jump, in the pattern of interference oscillations (Fig. 2). Similar experiments had been attempted many times but were previously confounded by the effects of strong Coulomb interactions between the bulk and the edge of the cavity. The crucial technical advance that made these experiments possible was the development of special-purpose high-mobility materials with nearby metallic layers to screen the Coulomb interactions [5].

In the first generation of these experiments, Nakamura and colleagues focused on the FQHE state at filling fraction $𝜈 = 1 ∕ 3$ [6]. The filling fraction, which is the ratio of the electron density to the density of magnetic flux quanta, is controlled by tuning the voltage and magnetic field. The data in the $𝜈 = 1 ∕ 3$ case looks delightfully clean. With precious little theoretical interpretation, one can clearly see phase jumps of approximately $2 𝜃 = 2 𝜋 ∕ 3$ , which are exactly what one expects when a single quasiparticle jumps into the middle of the cavity. Further, as a cross-check, the researchers show small corrections to the measured phase depending on the strength of the Coulomb interaction, which agrees well with theory. This verification gives one confidence that the experiment is actually measuring fractional statistics as claimed.

However, the devil’s advocate might say that the phase jumps in the $𝜈 = 1 ∕ 3$ case are not definitive proof of fractional statistics. The reason for the uncertainty is that the fractional charge is $q = 1 ∕ 3 \cdot e = 𝜈 e$ , and the fractional statistics phase angle is $2 𝜃 = 2 𝜋 ∕ 3 = 2 𝜋 𝜈$ . It’s possible, therefore, that the sudden interference changes are tied in some roundabout way to the filling factor or to the fractional charge and are not an effect related to the exchange interaction.

To resolve this ambiguity, Nakamura and colleagues have now performed an interferometer experiment at filling fraction $𝜈 = 2 ∕ 5$ [2]. This is a more complicated FQHE state having two edge modes rather than just one. With careful placing of voltage gates, the researchers were able to route edge states in such a way that they could target the particular edge modes that they wanted to measure. Consequently, they succeeded in extracting a fractional statistics angle of $2 𝜃 = - 4 𝜋 ∕ 5$ , as expected. What makes this measurement especially interesting is that this angle is not simply $2 𝜋 𝜈$ , which makes it far less likely that the interference signal was a consequence of something other than the fractional statistics.

While the results of this experiment are certainly not as crystal clear as the earlier experiments on $𝜈 = 1 ∕ 3$ [6], they still look fairly good. Similar to the data at $𝜈 = 1 ∕ 3$ , there are smooth oscillations interrupted by discrete phase slips, presumably from quasiparticles jumping into the cavity. The value of these phase slips seems to match fairly well with the expectation.

As with any good experiment, we may hope that nice results will beget even nicer results. We can also hope that what we learn from this experiment will lead to technology for doing even more sophisticated experiments in the future, such as interferometry of FQHE states with filling factor of $𝜈 = 5 ∕ 2$ . These states are harder to work with, but they might be useful in possible topological quantum computers.

References

J. M. Leinaas and J. Myrheim, “On the theory of identical particles,” Nuovo Cim. B 37, 1 (1977).
J. Nakamura et al., “Fabry-Pérot interferometry at the $𝜈 = 2 ∕ 5$ fractional quantum Hall state,” Phys. Rev. X 13, 041012 (2023).
R. E. Prange and S. M. Girvin, The Quantum Hall Effect (Springer, New York, 1990)[Amazon][WorldCat].
R. de Picciotto et al., “Direct observation of a fractional charge,” Nature 389, 162 (1997); L. Saminadayar et al., “Observation of the e/3 fractionally charged laughlin quasiparticle,” Phys. Rev. Lett. 79, 2526 (1997).
J. Nakamura et al., “Aharonov–Bohm interference of fractional quantum Hall edge modes,” Nat. Phys. 15, 563 (2019).
J. Nakamura et al., “Direct observation of anyonic braiding statistics,” Nat. Phys. 16, 931 (2020); “Impact of bulk-edge coupling on observation of anyonic braiding statistics in quantum Hall interferometers,” Nat. Commun. 13, 344 (2022).
H. Bartolomei et al., “Fractional statistics in anyon collisions,” Science 368, 173 (2020); M. Ruelle et al., “Comparing fractional quantum Hall Laughlin and Jain topological orders with the anyon collider,” Phys. Rev. X 13, 011031 (2023).
H. Kumar Kundu et al., “Anyonic interference and braiding phase in a Mach-Zehnder interferometer,” Nat. Phys. 19, 515 (2023).
J.-Y. M. Lee et al., “Partitioning of diluted anyons reveals their braiding statistics,” Nature 617, 277 (2023).
C. de C. Chamon et al., “Two point-contact interferometer for quantum Hall systems,” Phys. Rev. B 55, 2331 (1997).

About the Author

Steven H. Simon is a theoretical physics professor at the University of Oxford and a professorial fellow of Somerville College, University of Oxford. Previously, he was the director of theoretical physics research at Bell Laboratories. He has served on the UK EPSRC Physical Sciences Strategic Advisory Board. He is known for his work on topological phases of matter, topological quantum computation, and the fractional quantum Hall effect. He is the author of a popular introductory book on solid-state physics, The Oxford Solid State Basics, and a new book, Topological Quantum.