Seeking a Quantum Hall Effect for Light
Place a conductor in a magnetic field and the electrical current driven by an applied voltage will not flow in a straight line but in a direction perpendicular to the electric field—a behavior known as the Hall effect [1]. Reduce the temperature to the point where the electrons manifest quantum-mechanical behavior, and the plot thickens. The conductivity (defined as the ratio between the sideways current and the voltage) exhibits discrete jumps as the magnetic field is varied—the quantum Hall effect [2]. Since electrons at low temperature and photons obey a similar wave equation [3], should we also expect a quantum Hall effect for light? This question has been bubbling under the surface for the past decade, leading to the observation of some aspects of an optical quantum Hall effect [4, 5]. But the analogy between photons and electrons remains incomplete. Now a theoretical study by Mário Silveirinha from the University of Lisbon, Portugal, forges a new parallel between the physics of electrons and that of photons by defining the concept of a “photon conductivity” that characterizes the flow of light in response to the motion of matter [6]. Silveirinha’s innovative viewpoint on light–matter interaction could help researchers uncover a wealth of motion-induced wave effects.
The quantum Hall effect can be understood through the lens of topology—namely, through the link of the Hall conductance to topological invariants known as Chern numbers. In a conductor, the atoms form a periodic lattice, in which the behavior of electrons can be fully characterized through a single Brillouin zone—a primitive cell in the reciprocal, or momentum, space representation of the lattice. A convenient representation of such a Brillouin zone involves “cutting it out” from the momentum space and gluing its edges together to form a closed surface—a torus [7]. Each electron wave function in the conductor is then associated with a point on the surface of this torus. Chern numbers are integer numbers that tell us whether different sets of wave functions “attached” to the torus can be smoothly turned into each other [8]. One can show that the Hall conductivity can be expressed in terms of the product of several physical constants times a sum over these Chern numbers. Since these numbers are integers, the formula implies the conductivity’s quantization [7].
The topological description shows that the essential ingredients of the quantum Hall effect aren’t exclusive to electrons in magnetic fields. Integer Chern numbers can emerge for any kind of wave propagating through a periodic structure with a Brillouin zone that can be mapped onto the surface of a torus. This analogy has been enthusiastically recognized in the past decade, leading to a burst of research into engineered electromagnetic, acoustic, and elastic materials with nonzero Chern numbers of the bands characterizing wave propagation [9]. It is now well established, for instance, that, in analogy to the electronic edge states of a conductor in a magnetic field, nonzero Chern numbers can describe edge states for classical light waves propagating in systems such as photonic crystals [4].
Nevertheless, there are wrinkles. At least two missing ingredients make the connection between electrons and classical waves less than perfect. The first is fundamental: unlike classical electromagnetic waves, electrons are fermions and thus have half integer spin, obey the Pauli exclusion principle, and fill energy bands up to the so-called Fermi level. The second is the absence, in these classical systems, of a quantity that obviously corresponds to a conductance, let alone one that takes quantized values. Can one define a quantity that, like an electrical current, flows in response to an applied stimulus?
Silveirinha’s work answers this question for the case of electromagnetic waves. Understanding his approach involves inverting our usual perspective of light–matter interaction. While we are used to thinking of the electromagnetic field as producing charge acceleration, and thus currents, we are much less used to thinking of the reverse: the acceleration of matter can induce a flow of electromagnetic energy. Take radiation pressure, for instance. When an electromagnetic wave reflects from a mirror, the mirror will accelerate, leading to a flow of energy from the electromagnetic field to the mirror. We can understand this flow as a current of electromagnetic energy driven by the acceleration of matter—an idea fundamentally related to quantum phenomena such as the Unruh and the dynamic Casimir effects, in which the acceleration of a mirror in vacuum leads to the creation of a photon current [10]. Accounting for this relationship between mirror acceleration and electromagnetic energy flow, Silveirinha develops a mathematical formulation for a “photon conductivity.”
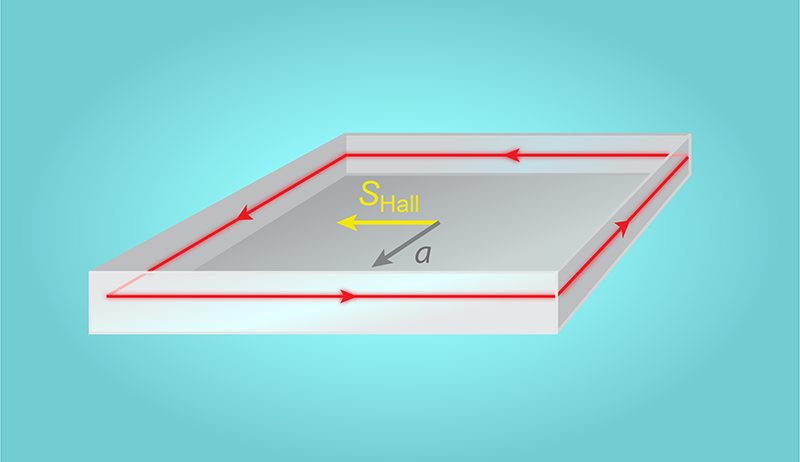
The definition allows him to uncover the possibility of a direct and unexpected light analog of the Hall effect. The researcher predicts that such effect emerges in a geometry where light is confined to an optical cavity containing an exotic crystal that is nonreciprocal, meaning that it behaves differently for forward and backward propagation (Fig. 1). In this configuration, the mechanical acceleration of the cavity is the counterpart of the electric field within a conductor, while the nonreciprocal medium plays the role of the magnetic field. Silveirinha demonstrates that, under appropriate conditions, there should be a sideways flow of electromagnetic energy—in analogy to the Hall effect for electrons. What’s more, he demonstrates that the topology of the band gaps of the periodic medium implies that this sideways conductivity is quantized—as in the quantum Hall effect.
For the time being, experiments to directly test this optical Hall effect are likely to be extremely difficult, as they require both exotic nonreciprocal materials and a large and precisely controllable acceleration of the cavity. And given the intricate mathematical expressions for the derived photon conductivity, it may take some time until the implications of this novel viewpoint will be fully appreciated. But the unifying perspective on wave physics offered by Silveirinha will likely open up new lines of inquiry. In particular, the novel definition of conductivity might be applicable to broader categories of systems than envisioned in this work, extending, for example, to acoustic and elastic materials where the presence of topological edge states has long been established.
References
- E. H. Hall, “On a new action of the magnet on electric currents,” Amer. J. Math. 2, 287 (1879).
- K. v. Klitzing et al., “New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance,” Phys. Rev. Lett. 45, 494 (1980).
- S. M. Barnett, “Optical Dirac equation,” New J. Phys. 16, 093008 (2014).
- S. Raghu and F. D. M. Haldane, “Analogs of quantum-Hall-effect edge states in photonic crystals,” Phys. Rev. A 78, 033834 (2008).
- K. Y. Bliokh et al., “Quantum spin Hall effect of light,” Science 348, 1448 (2015).
- M. G. Silveirinha, “Shaking photons out of a topological material,” Phys. Rev. B 108, 205142 (2023).
- D. J. Thouless et al., “Quantized Hall conductance in a two-dimensional periodic potential,” Phys. Rev. Lett. 49, 405 (1982).
- S.-S. Chern, “Characteristic classes of Hermitian manifolds,” Ann. Math. 47, 85 (1946).
- M. Kim et al., “Recent advances in 2D, 3D and higher-order topological photonics,” Light: Sci. Appl. 9, 130 (2020).
- D. A. R. Dalvit et al., “Fluctuations, Dissipation, and the Dynamical Casimir Effect,” Casimir Physics, edited by D. Dalvit et al. Lecture Notes in Physics (Springer, Berlin, Heidelberg, 2011) Vol. 834.