Signatures of Competing Cardiac Pacemakers
Our hearts maintain a steady beat thanks to the synchronization of electrical activity in cardiac cells. A team of researchers has explored one way in which this regularity can break down to generate a mixture of normal and abnormal beats: when two competing “pacemaker” regions pulse with different frequencies in the heart tissue [1]. Through experiments and theory, the researchers have identified telltale mathematical patterns of the resulting electrical waves. They say that their finding might help physicians spot this mechanism of aberrant beating in patients’ electrocardiogram recordings.
A collection of pacemaker cells in the heart produces periodic electrical waves—“sinus” pulses—that move across the tissue and cause coordinated contractions of the cardiac muscle. However, if a second (“ectopic”) pacemaker source appears elsewhere in the heart, an abnormal beating pattern called premature ventricular contraction (PVC) can be the result. PVCs have multiple causes and can sometimes lead to a life-threatening irregular heartbeat (arrhythmia). Physicians would like to distinguish benign PVCs from dangerous ones, but the first step is to simply identify the cause of a patient’s PVCs.
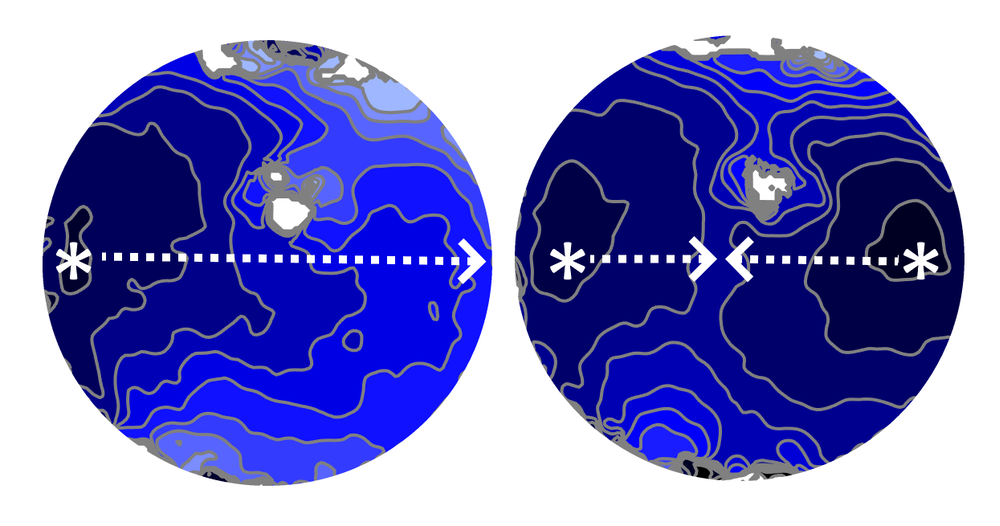
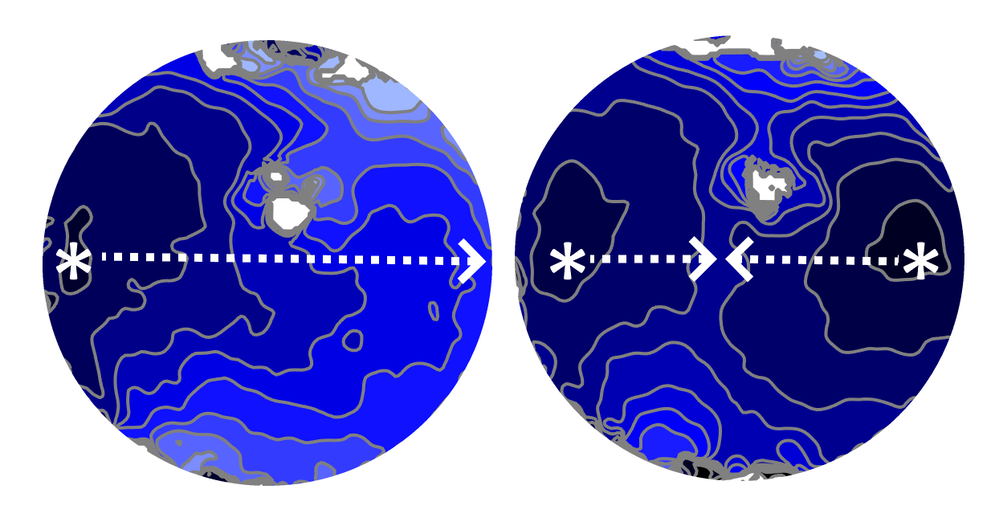
How two sets of waves from competing pacemakers interact in heart tissue is complicated. In 1986, physiologist Leon Glass of McGill University in Canada and his co-workers used a simple mathematical model to show that the resulting beating pattern is dictated by principles previously known in the mathematical discipline of number theory [2]. To better understand how this phenomenon manifests in a real heart, Glass and colleagues have now looked at the spatial pattern of the resulting electrical waves in a layer of mouse cardiac cells.
The researchers genetically modified the cells to allow the cell membrane voltages to be controlled using light. In this way, they could generate a pacemaker region with a particular frequency in a specified part of the tissue layer.
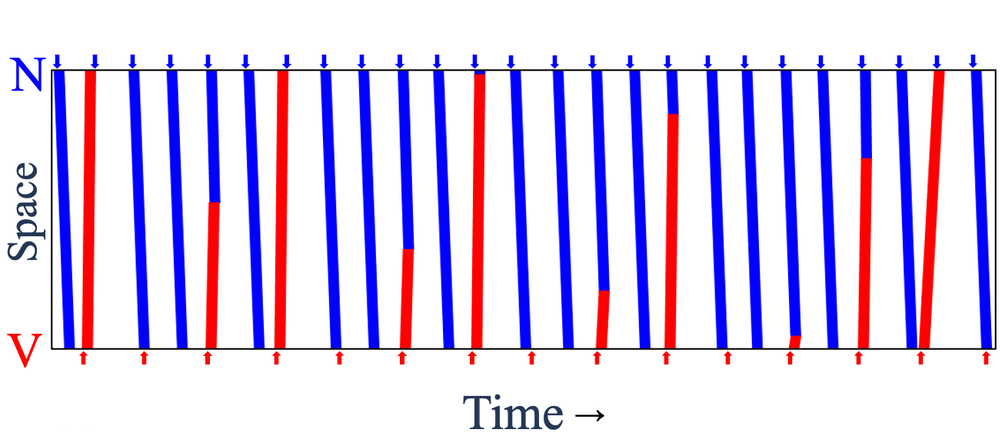
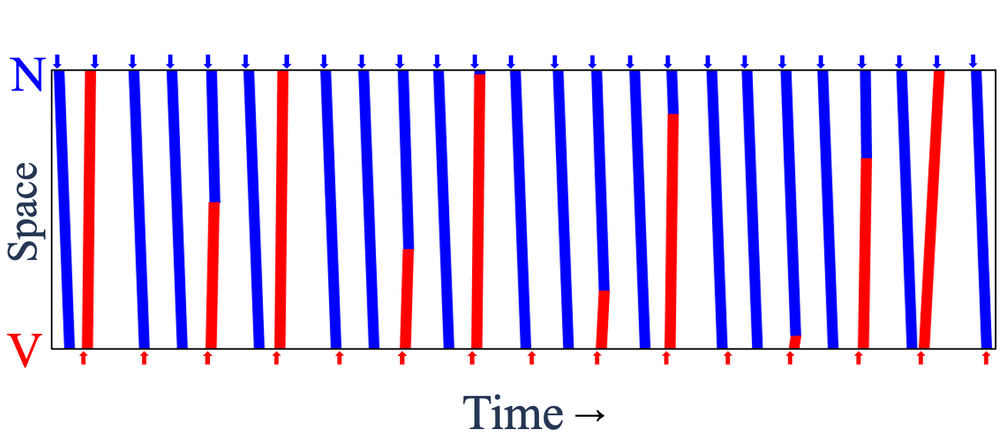
The researchers created a sinus pacemaker and a lower-frequency ectopic pacemaker about 8.5 mm apart and monitored the electrical activity in the region in between. Each pair of successive ectopic waves, or “beats,” had a certain number of intervening sinus beats (denoted NIB), which could vary from place to place and time to time because waves from the two sources often collided and canceled each other.
The team found that these NIB values in a given part of the tissue layer came in distinct triplets, such as 1, 4, 6—that is, there may be either 1, 4, or 6 intervening sinus beats between two ectopic beats. For all of the observed triplets, one number was odd, and the sum of the two smaller ones was one less than the largest number. “We do not have a simple, intuitive way to explain these numbers,” says team member and McGill graduate student Khady Diagne, but she adds that the same patterns occur in the number theory context too.
Glass and colleagues reproduced these patterns using a simple computational model called a cellular automaton consisting of a chain of cells that are switched between three different states according to the states of their neighbors. The triplets of NIB values appear in this model too. The researchers show that such triplets are picked out in a mathematical analysis of interacting oscillators.
The team says that these NIB triplets are a signature of the presence of an ectopic pacemaker interacting with the normal sinus pacemaker, which is one of the causes of PVCs. To look for that signature in real data, the researchers examined heart electrical recordings (electrocardiograms, or ECGs) from 47 patients known to experience regular PVCs. Eight of the patients were found to have ECGs with NIB values corresponding to one of the triplets in the model (such as 1, 4, 6), suggesting that those patients’ PVCs could be caused by the dual-pacemaker mechanism. Diagne says the team hopes that a future wearable heartbeat monitor might identify both this and other mechanisms of PVCs and might ultimately enable clinicians to evaluate the resulting health risk.
“The most wonderful thing about this work is that their mathematical model is extremely simple, and yet it accounts in surprising detail for what they see in their experiments,” says Steven Strogatz of Cornell University, a specialist in the mathematics of complex and nonlinear systems. “It’s a beautiful case study of the power of mathematics to illuminate otherwise puzzling phenomena in biology and medicine.”
“The comparison of cellular automaton simulations and experiments is remarkable given the simplicity of the model and the complexity of cardiac biology,” says Alain Karma, a specialist in the physics of complex systems at Northeastern University in Boston. He believes that the theory “holds promise for understanding [PVCs] in a clinical setting.”
–Phillip Ball
Philip Ball is a freelance science writer in London. His latest book is How Life Works (Picador, 2024).
References
- K. Diagne et al., “Rhythms from two competing periodic sources embedded in an excitable medium,” Phys. Rev. Lett. 130, 028401 (2023).
- L. Glass et al., “Dynamics of pure parasystole,” Am. J. Physiology 251, H841 (1986).