Evidence Found for a Majorana “Cousin”
The search for Majorana fermions—exotic quantum states that have the potential to revolutionize quantum computing—has been anything but straightforward. Experimental hints of the states were first seen in 2012. In 2018, researchers at a Microsoft laboratory in the Netherlands claimed they had unequivocal experimental evidence for Majorana fermions but later retracted their claim. Now a team containing some of the researchers on that 2018 study has found evidence for a cousin of the Majorana fermion, the so-called poor man’s Majorana [1]. The team anticipates that the finding will revive the field and the hunt for these elusive states.
When the experimental realization of the Majorana fermion was retracted, “there was a crisis in the Majorana field,” says Tom Dvir of Delft University of Technology, Netherlands, and a researcher on the new study. “We hope that our finding will help refocus efforts.”
The Majorana fermion is a hypothetical collective electronic state that acts like a particle that is its own antiparticle. Theorists predict that Majorana fermions are topologically protected, which makes them robust to thermal or electrical perturbations from the environment. The poor man’s Majorana is also its own antiparticle, but it lacks the Majorana’s topological protection. This difference means that the poor man’s Majorana’s is only stable for a very small range of parameters, says Dvir.
The Majorana fermion’s topological protection comes because of the highly localized nature of the state—in a nanowire, a popular system for Majorana searches, Majorana states are predicted to be bound to the two ends of the wire. This localization means that if the positions of two Majoranas are swapped, the states don’t interact and thus retain their original encoding. This property is what makes the states interesting for qubits, as operations could be performed with the qubits without noise degrading or changing the information that they contain. Poor man’s Majoranas, however, behave a little like leaky Tupperware boxes—put two in your bag and their contents will spill and mix. “They can exchange information,” Dvir says. But some researchers think that realizing these “poorer” states is still an important step in the goal of Majorana-based quantum computing. “The system is imperfect, but we could make a qubit out of it and then learn how that qubit behaves,” Dvir says.
Dvir and his colleagues realize their poor man’s Majoranas in a quantum-dot device in which two quantum dots are connected via a semiconducting wire that is coated with a superconducting film. This device is the shortest possible realization of a Kitaev chain—a 1D chain of fermions with zero spin. When longer—five quantum dots or more—the Kitaev chain should host topological Majoranas.
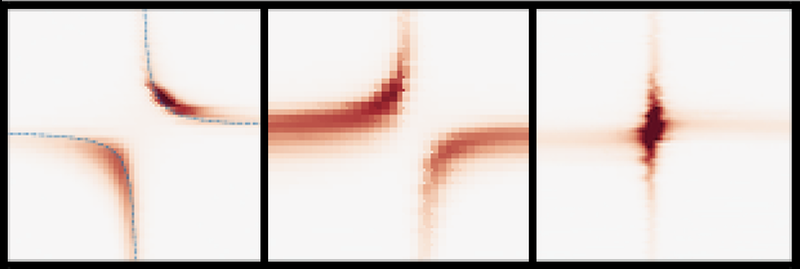
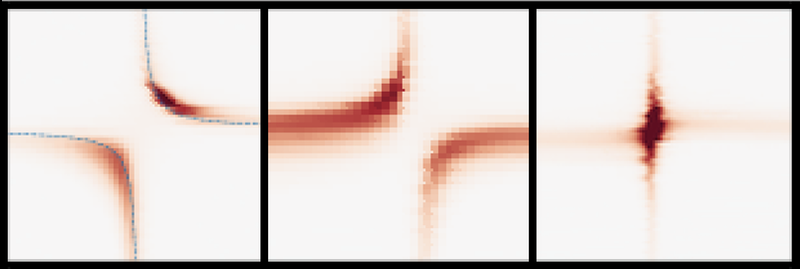
When electrons in a minimal Kitaev chain move between the quantum dots they do so via one of two processes: normal tunneling, where the electrons simply hop from one dot to the other; or Andreev tunneling, where electrons from the two dots simultaneously enter the superconductor. There they join to form a Cooper pair that is then injected into both dots, connecting them. Kitaev predicted that when the normal and Andreev tunneling rates match, Majorana states appear.
Dvir and his colleagues show that this is indeed the case. They demonstrate that by tuning the voltages applied to each element in their device, they can electrically switch the device from a regime where normal tunneling dominates to one where Andreev reflection dominates to one where the two processes have equal rates. In their experiments, they detected the signals of all these regimes and those predicted for the two poor man’s Majorana states.
This demonstration is the first of a poor man’s Majorana, says Karsten Flensberg of the University of Copenhagen in Denmark, one of the theorists who predicted that this quantum-dot system would host poor man’s Majoranas [2]. “The [researchers] came up with an ingenious way to tune the ratio of normal tunneling and Andreev tunneling between the two quantum dots.” Previous proposals for connecting the dots and tuning the system involved multiple magnetic fields, which Flensberg notes are difficult to control with the nanoscale precision required for Majorana experiments. By using the superconductor and electric gates, the team got around this problem. “It is a breakthrough in Majorana research,” he says. That sentiment is echoed by Jagadeesh Moodera, an experimentalist at the Massachusetts Institute of Technology who is actively searching for topological Majoranas. The new platform “opens a new frontier in the study of Majorana physics,” he says. Majorana research “has been mired in some controversy and it is refreshing to see good basic science being done on [this topic].”
The demonstration does however have a limitation. The wave functions of the two realized poor man’s Majorana appear to slightly overlap, meaning that they aren’t completely confined to their respective quantum dots. “The states are imperfect,” Dvir says. Dvir notes, however, that it is unclear if the imperfection matters for qubits based on poor man’s Majoranas; they are working with theorists to find that out. Flensberg hopes that researchers will also investigate other qubit-related properties of this system. “It is not a priori clear that topologically protected Majorana are better [for quantum computing],” he says.
For Dvir, this realization of a poor man’s Majorana is special for another reason. For most physics experiments, significant analysis and interpretation is required to go from experimental data to a plot that can be compared to the output of a theoretical model. “It’s rare that abstract physics appears in the lab exactly as predicted,” he says. “Here we see it with no interpretation; it’s really fun.”
–Katherine Wright
Katherine Wright is the Deputy Editor of Physics Magazine.
References
- T. Dvir et al., “Realization of a minimal Kitaev chain in coupled quantum dots,” Nature 614, 445 (2023).
- M. Leijnse and K. Flensberg, “Parity qubits and poor man’s Majorana bound states in double quantum dots,” Phys. Rev. B 86, 134528 (2012).