Probing the Helium Nucleus beyond the Ground State

Evgeny Epelbaum

Viewpoint

Probing the Helium Nucleus beyond the Ground State

Evgeny Epelbaum

Faculty of Physics and Astronomy, Ruhr University Bochum, Bochum, Germany

April 10, 2023• Physics 16, 58

A new electron-scattering experiment challenges our understanding of the first excited state of the helium nucleus.

Figure caption — **Figure 1:** Inelastic electron scattering off helium nuclei can provide information about the first excited state of helium, which is called $0_{2}^{+}$ . New experiments confirm a discrepancy with theoretical predictions.

A helium nucleus, also known as an $𝛼$ particle, consists of two protons and two neutrons and is one of the most extensively studied atomic nuclei. Given the small number of constituents, the $𝛼$ particle can be accurately described by first principles calculations. And yet, the excited states of the $𝛼$ particle remain a bit of a mystery, as evidenced by a disagreement surrounding the excitation from the ground state $0_{1}^{+}$ to the first excited state $0_{2}^{+}$ [1]. Theoretical predictions for this transition do not match measurements, but the experimental uncertainties have been too large for implications to be drawn. Now, the A1 Collaboration at Mainz Microtron (MAMI) in Germany has remeasured this transition via inelastic electron scattering [2]. The new data significantly improves the precision compared to previous measurements and confirms the initial discrepancy. The results yield new insights into the spatial structure of the $0_{2}^{+}$ state while touching on fundamental questions about our understanding of nuclear interactions.

Low-energy properties of nuclei can be studied by solving the quantum mechanical Schrödinger equation for interacting nucleons. Recent progress in ab initio few-body methods, coupled with rapidly increasing computational power, allow for a reliable description of light- and medium-mass nuclei [3]. The currently most established approach is based on chiral effective field theory ( $𝜒$ EFT) [4]. This theory allows one to derive nuclear interactions via a perturbative expansion in quark masses and in the three momenta of the nucleons. It offers a natural explanation of the observed hierarchy of nuclear forces, in which two-nucleon interactions dominate multinucleon interactions. $𝜒$ EFT has been successfully and extensively applied to a wide range of nuclear systems [5].

For the $𝛼$ particle, the energy of the $0_{1}^{+}$ ground state is correctly reproduced in $𝜒$ EFT calculations. But as it turns out, the ground-state energy is driven by universal properties of few-nucleon systems [6] and, therefore, it is largely insensitive to details of the interaction. A more rigorous test comes from reproducing the electric form factor $𝓕 (Q^{2})$ , which depends on the four-momenta transfer $Q$ and can be interpreted as a measure of charge distribution within the nucleus. Theoretical calculations of $𝓕 (Q^{2})$ for the $𝛼$ particle and other light nuclei demonstrate good agreement with experimental data at low $Q^{2}$ values [7], indicating that the ground-state structure of these nuclei is well understood. Low-energy scattering of two $𝛼$ particles is also appropriately described using $𝜒$ EFT [8].

The $𝛼$ particle can be excited from its ground state to the $0_{2}^{+}$ state with an energy of 20.2 MeV, which lies slightly above the two-body breakup threshold of 19.8 MeV—where the $𝛼$ particle breaks up into a proton and a hydrogen-3 nucleus. It might seem strange that $0_{2}^{+}$ lies in the “continuum” of unbound states, but this above-threshold situation is common in nuclear physics, which is why many excited states are referred to as resonances. Given the above-threshold energy, researchers still debate how to interpret the $0_{2}^{+}$ state: is it predominantly a collective excitation of the four-nucleon system or is it a molecular-like state consisting of the proton and a hydrogen-3 nucleus?

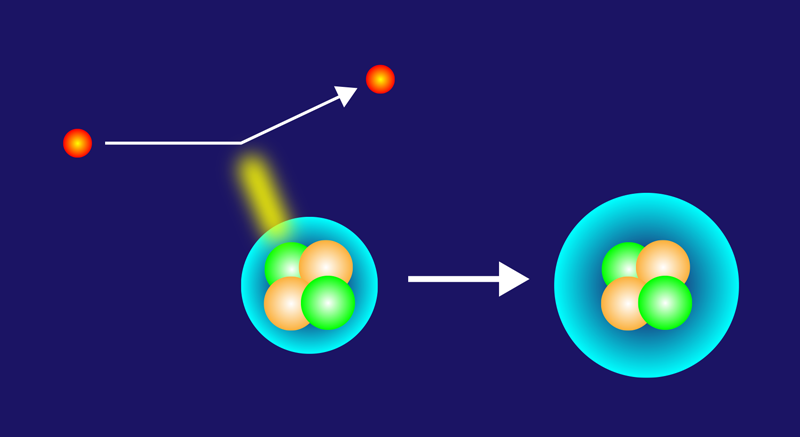
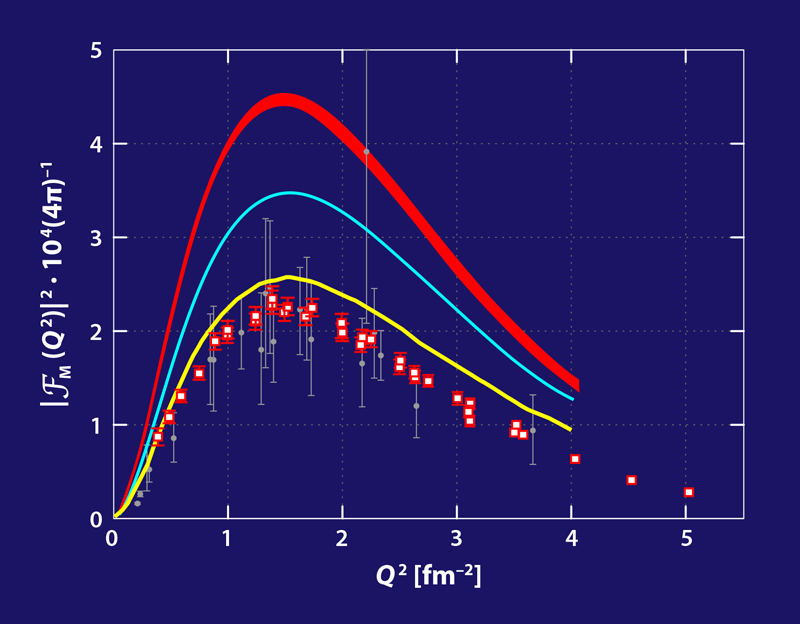
To help understand the $0_{2}^{+}$ state, experimentalists can probe this resonance with inelastic electron scattering (Fig. 1), recovering the so-called monopole transition form factor $𝓕_{M} (Q^{2})$ , which is sensitive to the structure of the excited state. Several experiments in the 1970s measured the square of the absolute value of $𝓕_{M}$ for a range of $Q^{2}$ values. On the theory side, calculations of the form factor have been challenging because of the location of the $0_{2}^{+}$ state above the continuum threshold, as most ab initio calculations are limited to bound states. This complication was overcome in 2013 using a technique that implicitly takes into account continuum effects [1]. The calculations using $𝜒$ EFT—as well as phenomenological models—were found to disagree with the data, but no strong conclusions could be drawn due to the low precision of the experimental data taken almost half a century ago.

Simon Kegel from the Johannes Gutenberg University Mainz, Germany, and colleagues have now measured the monopole form factor over a broad range of $Q^{2}$ values with strongly reduced uncertainties compared to previous measurements [2]. To achieve this improvement, the team exposed a helium gas target in an aluminum cell to the MAMI electron beam at three different energies. The essential element of the analysis was a careful treatment of background contributions caused by scattering of electrons on the aluminum cell walls. To isolate this background, the team performed separate measurements with strongly reduced helium density inside the cell. The new high-precision data for the transition form factor agree with the previous measurements and confirm the disagreement with the calculations (Fig. 2). Kegel and his colleagues have also extracted the first two coefficients in the low-momentum expansion of the transition form factor. These quantities, which provide information about the spatial extension of the $0_{2}^{+}$ state, were also found to deviate from theoretical predictions.

So, what do these discrepancies imply for the modern theory of nuclear forces? First of all, the predictions for the transition form factor differ by about 100%, depending on the interaction inputs used. This large spread in theoretical predictions suggests that the form factor may serve as a tool, or “magnifying glass,” for probing small contributions to nuclear forces [1]. However, before such analysis can be done, researchers need a better understanding of the theoretical uncertainties. In contrast to phenomenological models, $𝜒$ EFT provides a systematic order-by-order expansion of low-energy observables and permits estimation of the truncation error from neglected higher-order interactions. In recent years, Bayesian methods have been developed to quantify truncation errors by “learning” how the $𝜒$ EFT expansion converges as more orders are calculated [9]. If future work shows that these truncation errors are large for the transition form factor, as already suggested by its extreme sensitivity to the interaction inputs, then the significance of the observed discrepancy may be called into question.

Regardless of the uncertainty issues discussed above, the origin of the strong sensitivity of the form factor to details of the nuclear force is an interesting question in itself. One possible explanation relates to how close the $0_{2}^{+}$ excitation energy (20.2 MeV) is to the two-body breakup threshold (19.8 MeV). The form factor may depend on this energy difference, so any uncertainties in calculating the excitation energy would translate into relatively large uncertainties in the form factor predictions. Recently, researchers extracted the characteristics (energy and width) of the $0_{2}^{+}$ resonance from the proton-plus-hydrogen-3 phase shifts by solving the four-body scattering problem using $𝜒$ EFT [10]. In line with the suggested explanation, the width of the $0_{2}^{+}$ resonance was found to exhibit a very strong sensitivity to the details of the interactions. Further theoretical research is needed to explore the relationship between the form factor and the location of the $0_{2}^{+}$ resonance.

References

S. Bacca et al., “Isoscalar monopole resonance of the alpha particle: A prism to nuclear Hamiltonians,” Phys. Rev. Lett. 110, 042503 (2013).
S. Kegel et al., “Measurement of the $𝛼$ -particle monopole transition form factor challenges theory: A low-energy puzzle for nuclear forces?” Phys. Rev. Lett. 130, 152502 (2023).
H. Hergert, “A guided tour of ab initio nuclear many-body theory,” Front. Phys. 8 (2020).
S. Weinberg, “Nuclear forces from chiral lagrangians,” Phys. Lett. B 251, 288 (1990).
E. Epelbaum et al., “Modern theory of nuclear forces,” Rev. Mod. Phys. 81, 1773 (2009).
E. Braaten and H.-W. Hammer, “Universality in few-body systems with large scattering length,” Phys. Rept. 428, 259 (2006).
L. E. Marcucci et al., “Electromagnetic structure of few-nucleon ground states,” J. Phys. G: Nucl. Part. Phys. 43, 023002 (2016).
S. Elhatisari et al., “Ab initio alpha–alpha scattering,” Nature 528, 111 (2015).
R. J. Furnstahl et al., “Quantifying truncation errors in effective field theory,” Phys. Rev. C 92, 024005 (2015).
M. Viviani et al., “n + ³H, p + ³He, p + ³H, and n + ³He scattering with the hyperspherical harmonic method,” Phys. Rev. C 102, 034007 (2020).

About the Author

Evgeny Epelbaum received his PhD in 2000 from Ruhr University Bochum, Germany, and worked as a postdoctoral researcher at the Ruhr University Bochum, Forschungszentrum Jülich in Germany, the Paris-Sud University, and the Jefferson Lab in Virginia. In 2006, he became an associate professor at the University of Bonn, Germany. Since 2010, he has been a full professor of theoretical physics at the Ruhr University Bochum. His research focuses on understanding the structure and dynamics of strongly interacting hadronic and nuclear systems using effective field theory. He is a recipient of the 2021 Faddeev Medal.