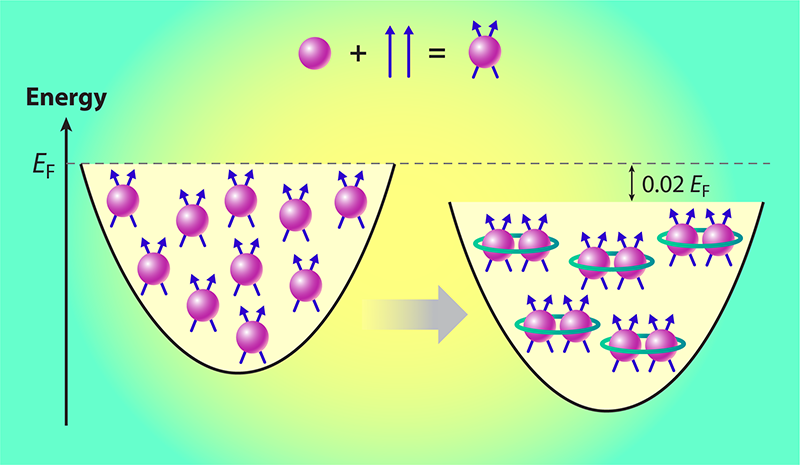
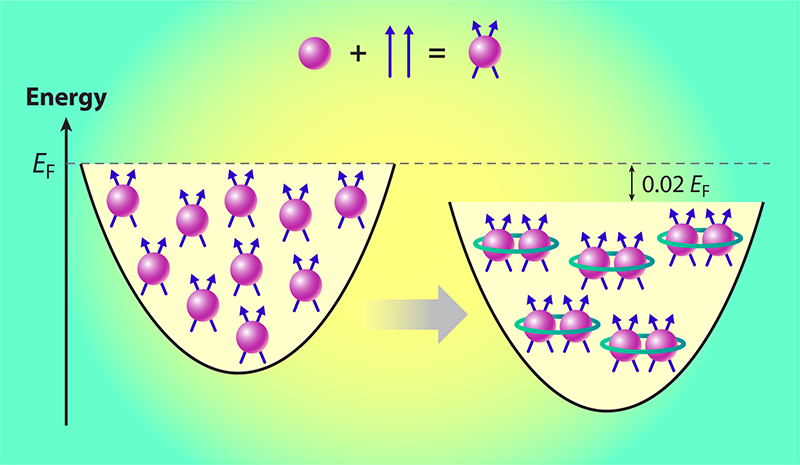
Composite Fermions Are Better Together

Noah Bray-Ali

Viewpoint

Composite Fermions Are Better Together

Physical Sciences Department, Mount Saint Mary’s University-Los Angeles, Los Angeles, CA, US

January 22, 2024• Physics 17, 10

Particle pairing seen in nanoscale semiconductor devices could point the way to materials that superconduct at high temperatures.

Figure caption — **Figure 1:** If an electron liquid flows in a strong magnetic field, its electrons (purple) can capture an even number of magnetic-flux quanta (blue) to form exotic particles known as composite fermions. Usually, each particle has a maximum energy given by the so-called Fermi energy *E_F*. Sharma and colleagues argue that, if the flux quanta add up to a field whose strength roughly matches that of the external field, the composite fermions pair up [3]. This pairing releases an energy of 0.02 *E_F* per particle and induces the fractional quantum Hall effect, whereby the liquid flows without heat loss.

In 1986, materials physicists discovered a new kind of superconductor that is surprisingly resilient to heat, electrical currents, and magnetic fields [1]. Six years later, device physicists found something similar in a nanoscale semiconductor device: an incompressible electron liquid, known as a fractional quantum Hall fluid, that flows without heat loss at much higher temperatures than expected [2]. Now, after more than 30 years, Anirban Sharma at Pennsylvania State University, University Park, and colleagues think they have developed the right picture to help scientists understand the properties of this electron liquid (Fig. 1) [3]. The picture might shed light on the way electrons form pairs to flow without energy dissipation in high-temperature superconductors.

When an electron travels through a magnetic field with strength B and with a direction perpendicular to the particle’s velocity, it moves in a circle. What sets the extreme quantum limit, called the magnetic length l_B, for the radius of the smallest possible circle? As Niels Bohr could have guessed and as Lev Landau showed [4], the quantum of angular momentum given by Planck’s constant h does the trick when it is combined with the electron charge e: their ratio h/e = 4.14 × 10^–¹⁵ T m² can be expressed as 2 $𝜋$ Bl_B². For electrons moving in a magnetic field of roughly 15 T, the magnetic length is only about 7 nm. It is under these conditions that fractional quantum Hall fluids were first found more than 40 years ago in nanoscale semiconductor devices known as quantum wells [5].

In 2023, fractional quantum Hall fluids were seen for the first time without an applied magnetic field by having the electrons instead move within a magnetic semiconductor device [6]. Yet, the basic physical picture remains the same (Fig. 1). Each electron captures an even number of magnetic-flux quanta from the surrounding electron liquid, resulting in a composite object called a composite fermion. But what happens when the little bits of magnetic flux attached to each electron add up to a field that roughly matches that of the magnet or magnetic semiconductor device in which the fluid flows? The composite-fermion liquid effectively “feels” no net magnetic field, yet it still condenses into a fractional quantum Hall fluid, as was found back in 1992 [2].

In a nanoscale semiconductor device with static dielectric constant $𝜀$ , a pair of composite fermions separated by the magnetic length will create static electricity of energy e²/ $𝜀$ l_B. This energy sets the fundamental temperature scale of a fractional quantum Hall fluid. For a typical device made with the semiconducting material gallium arsenide in a 15-T magnet, the temperature scale works out to 23 K [2]. However, experiments have shown that actual devices must be cooled to about 2 K to manifest the fractional quantum Hall effect, in which the composite fermions flow without heat loss [5].

Sharma and colleagues took this real-world energy scale of about 0.1 e²/ $𝜀$ l_B as the composite-fermion liquid’s Fermi energy E_F [3]. Here, E_F corresponds to the maximum kinetic energy that a composite fermion in the liquid at zero net magnetic field would have if the potential energy from static electricity were “turned off” by cranking up the dielectric constant to infinity. The researchers argue that the composite fermions pair up and that the pairing releases an energy of 0.02 E_F per particle (Fig. 1). This estimate, if correct, means that these pairs of particles are around 20 times more stable than the electron pairs responsible for superconductivity in almost all known materials. When measured relative to the Fermi energy, the energy released during the pairing of composite fermions in zero net magnetic field would instead be roughly comparable to the pairing energy seen in the highest-temperature superconductors yet found [1].

Perhaps the clearest and most pressing test of Sharma and colleagues’ argument could be performed in the magnetic semiconductor devices in which the fractional quantum Hall effect was recently seen without an applied magnetic field [6]. To do so, however, major improvements to the quality of the devices will likely be needed. For instance, the ability of an electron to flow in circles—known as the electron mobility—is roughly 100 times lower in these new devices than it was in the devices that led to the discovery of the fractional quantum Hall effect [2].

A less-clear, but more far-reaching, direction for future work concerns the difference in scale between the fundamental energy e²/ $𝜀$ l_B set by the static electricity of a pair of composite fermions and the much lower Fermi energy E_F = 0.1 e²/ $𝜀$ l_B set by the temperature at which the fractional quantum Hall effect manifests in actual devices. Assuming Sharma and colleagues’ argument is correct, their result can just as well be interpreted to say that, relative to the pairing energy per particle, the Fermi energy of composite fermions in nanoscale semiconductor devices is 20 times smaller than that of the electrons that pair up in a typical superconducting material. A step forward—which surprisingly has not yet been taken—would be to directly measure the Fermi energy of composite fermions in high-quality gallium arsenide devices. One could then verify if it is indeed 10 times smaller than the static electric energy of a pair of composite fermions separated by the magnetic length.

References

J. G. Bednorz and K. A. Müller, “Possible highT_c superconductivity in the Ba-La-Cu-O system,” Z. Phys. B 64, 189 (1986).
Y. W. Suen et al., “Observation of a $𝜈$ =1/2 fractional quantum Hall state in a double-layer electron system,” Phys. Rev. Lett. 68, 1379 (1992).
A. Sharma et al., “Composite-fermion pairing at half-filled and quarter-filled lowest Landau level,” Phys. Rev. B 109, 035306 (2024).
L. Landau, “Diamagnetismus der Metalle,” Z. Physik 64, 629 (1930).
D. C. Tsui et al., “Two-dimensional magnetotransport in the extreme quantum limit,” Phys. Rev. Lett. 48, 1559 (1982).
J. Jain, “In a twist, composite fermions form and flow without a magnetic field,” Physics 16, 163 (2023).
M. R. Peterson et al., “Fractional quantum Hall effects in bilayers in the presence of interlayer tunneling and charge imbalance,” Phys. Rev. B 82, 235312 (2010).

About the Author

Noah Bray-Ali is a lecturer in the Physical Sciences Department of Mount Saint Mary’s University-Los Angeles. He earned a PhD in physics from the University of California, Berkeley, in 2006 for work on low-dimensional and strongly correlated electron systems. He then held postdoctoral positions in condensed-matter physics, quantum information science, and atomic physics. Recently, he has worked on resolving long-standing tensions and large-scale discrepancies between the standard model of particle physics and precision measurements of fundamental particle properties using accelerated particle beams in colliders and storage rings.