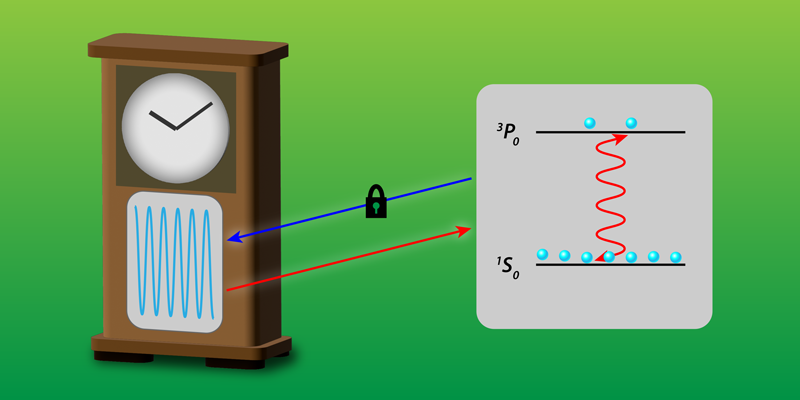
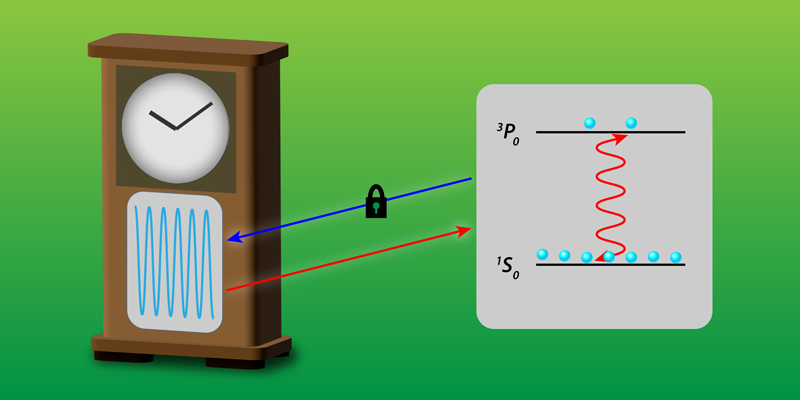
Reducing Uncertainty in an Optical Lattice Clock

Han-Ning Dai; Yu-Ao Chen

Viewpoint

Reducing Uncertainty in an Optical Lattice Clock

School of Physical Sciences, University of Science and Technology of China, Hefei, China

July 29, 2024• Physics 17, 118

By reducing the effect of systematic errors, researchers have created an atomic clock that sets a new record for precision.

Figure caption — **Figure 1:** A transition between the ¹S₀ and ³P₀ states of a strontium atom acts as the reference for the optical lattice clock. When a light signal is resonant with the transition, its frequency can be defined very precisely.

The advent of atomic clocks in the 1950s marked a paradigm shift in our ability to measure time with ultrahigh precision. Today’s most precise devices are so accurate that, if you had started one ticking at the big bang, it would by now be off by barely a second. These precise clocks have found various applications in fields such as fundamental physics [1], metrology [2], and navigation [3]. Further improvements could lead to a host of new applications and new tests of fundamental physics. However, achieving such improvements is fraught with challenges, primarily stemming from environmental noise, such as magnetic fluctuations and temperature variations, and from difficulties in manipulating the intricate atomic interactions that govern the clock’s operation. Tackling these challenges, a team of researchers from JILA in Colorado and the University of Colorado Boulder has broken the record for the precision of an atomic clock [4]. Using an optical lattice clock (OLC) based on neutral strontium atoms, the team measured the frequency of an atomic transition with a systematic uncertainty of 8.1 $\times$ 10⁻¹⁹, an improvement of more than a factor of 2 over the previous record holder, another strontium OLC [5]. This achievement signifies a leap in timekeeping accuracy, setting the benchmark for the next generation of atomic clocks.

The first atomic clocks marked time using the frequency of a microwave signal as their “pendulum.” Nowadays, the best technology for timekeeping is based on the light emitted by certain atomic transitions known as clock transitions. The high frequencies (typically several hundreds of terahertz) and narrow linewidths (typically 1–100 mHz) of these transitions mean that optical atomic clocks can measure time with greater precision than microwave-based atomic clocks, which tick at lower frequencies. Thanks to the efforts of researchers over the past few decades [4, 6], optical clocks now outperform those earlier devices by more than 2 orders of magnitude. Improving their performance even further means reducing the size of systematic errors.

Working toward this goal, the team from JILA and the University of Colorado Boulder has reevaluated the coefficients of certain atomic parameters that are critical for an optical atomic clock’s operation. In particular, the researchers performed a precise calibration of the second-order Zeeman coefficient on the least magnetically sensitive clock transition in strontium atoms—the transition between the ³P₀ and ¹S₀ states (see Fig. 1). The Zeeman coefficients describe the effect of a magnetic field on electronic energy levels, and therefore on the frequency of light that is emitted during the relevant transition. Typically, magnetically insensitive clock transitions are chosen so that the dominant first-order Zeeman frequency shift is minimized. Such minimization reduces the clock’s sensitivity to environmental magnetic fluctuations. But weaker second-order effects remain. The team’s calibration of this coefficient reduces the uncertainty due to the second-order Zeeman shift to 1 $\times$ 10⁻¹⁹, a twofold improvement compared to previous such calibrations.

The researchers also addressed a second factor contributing to clock uncertainty: the so-called dynamic black-body-radiation correction. Black-body radiation can shift an atom’s energy levels via the radiation’s electric field, an unavoidable consequence of operating the clock in a room-temperature environment. The dynamic component of this effect refers to the differential shift between an atom’s energy levels. In previous generations of strontium OLCs, accuracy was limited especially by the uncertainty in the shift of the ³P₀ level, the upper of the two states defining the clock transition. The size of this shift is tied to a transition whose energy lies within the energy spectrum of the black-body radiation—a transition between ³P₀ and a higher-energy state ³D₁—and can be determined by measuring the ³D₁ state’s lifetime. By making such measurements, the team reduced the uncertainty in the black-body-radiation shift to 7.3 $\times$ 10⁻¹⁹ (down from the 1.5 $\times$ 10⁻¹⁸ value that they achieved previously). Combining the reduction of black-body-radiation shifts with other environmental control measures such as temperature stabilization, the researchers determined the sum of all systematic effects on the clock transition’s energy levels to be less than one part in 1 $\times$ 10¹⁸.

To control and measure the atoms in their OLC, the researchers used an optical lattice with a “magic wavelength.” In an optical lattice trap, the atoms’ energy levels can be shifted by the electric fields of the laser beams. In a trap operating at the magic wavelength, however, the trapping potential is the same for all atoms regardless of their electronic state. This means that the relative energy shift that the laser beams induce between the clock transition states is minimized, which helps to make the transition’s linewidth as narrow as possible. The researchers also implemented a cooling process that allowed them to confine the atoms using a shallow lattice. The size of the energy shift induced by the laser beams is greater when the atoms are more tightly confined, so the shallow potential minimized such shifts.

These methodologies enable their device to surpass the precision of all previous OLCs, with a timekeeping error of less than a second over 39.6 billion years. The implications of this improvement are profound. For example, a new generation of instruments incorporating the Colorado team’s advances could help set a new benchmark for the definition of the second [7]. Future efforts may focus on refining these techniques, further reducing uncertainties by, for example, cryogenic operation [8]. The newfound precision could be employed to delve into fundamental problems at the frontiers of physics research, potentially shedding light on the quantum nature of gravity through gravitational-wave observations [9] as well as on the nature of dark matter [4, 10].

References

A. Derevianko and M. Pospelov, “Hunting for topological dark matter with atomic clocks,” Nat. Phys. 10, 933 (2014).
J. Grotti et al., “Geodesy and metrology with a transportable optical clock,” Nat. Phys. 14, 437 (2018).
J. M. Dow et al., “The International GNSS Service in a changing landscape of Global Navigation Satellite Systems,” J. Geod. 83, 191 (2009).
A. Aeppli et al., “Clock with 8 $\times$ 10⁻¹⁹ systematic uncertainty,” Phys. Rev. Lett. 133, 023401 (2024).
T. Bothwell et al., “JILA SrI optical lattice clock with uncertainty of 2.0 $\times$ 10⁻¹⁸,” Metrologia 56, 065004 (2019).
E. Oelker et al., “Demonstration of 4.8 $\times$ 10⁻¹⁷ stability at 1 s for two independent optical clocks,” Nat. Photonics 13, 714 (2019).
F. Riehle et al., “The CIPM list of recommended frequency standard values: Guidelines and procedures,” Metrologia 55, 188 (2018).
I. Ushijima et al., “Cryogenic optical lattice clocks,” Nat. Photonics 9, 185 (2015).
S. Kolkowitz et al., “Gravitational wave detection with optical lattice atomic clocks,” Phys. Rev. D 94, 124043 (2016).
C. J. Kennedy et al., “Precision metrology meets cosmology: Improved constraints on ultralight dark matter from atom-cavity frequency comparisons,” Phys. Rev. Lett. 125, 201302 (2020).

About the Authors

Han-Ning Dai is a professor of physics at the University of Science and Technology of China (USTC). He obtained his PhD from the USTC and completed a postdoc at the University of Heidelberg, Germany. His research group at the USTC performs experiments related to a range of topics in atomic, molecular, and optical physics, including ultracold lattice gases and quantum metrology.

Yu-Ao Chen is a professor at the University of Science and Technology of China (USTC). He obtained a doctoral degree from the University of Heidelberg, Germany, and he has conducted research at the University of Heidelberg, the University of Mainz, and the Max Planck Institute for Quantum Optics, all in Germany. His current research focuses on quantum manipulation of photons and atoms including multiphoton entanglement, ultracold atoms in optical lattices aiming at quantum simulation of many-body physics, and quantum metrology.