Constraining Many-Body Localization
A foundational tenet of statistical physics is the ergodic hypothesis, which states that macroscopic systems eventually explore all allowed microscopic configurations. Its far-reaching consequences include the impossibility of perpetual motion and the arrow of time. However, not all physical systems are ergodic. Systems with microscopic inhomogeneity can get stuck in certain configurations with striking consequences for their macroscopic properties. In both classical and quantum systems, the theoretical description of these nonergodic systems is incomplete. Simple models exhibit intricate phases with varying degrees of nonergodicity, but it is unclear how much they teach us about real-world systems. Two years ago, Alan Morningstar, now at Global Quantitative Strategies in Chicago, and colleagues identified several important regimes in inhomogeneous quantum systems and reconciled tensions between theoretical predictions and numerical observations [1]. Their research has since stimulated probes of nonergodicity and revitalized attempts to connect quantum and classical glasses.
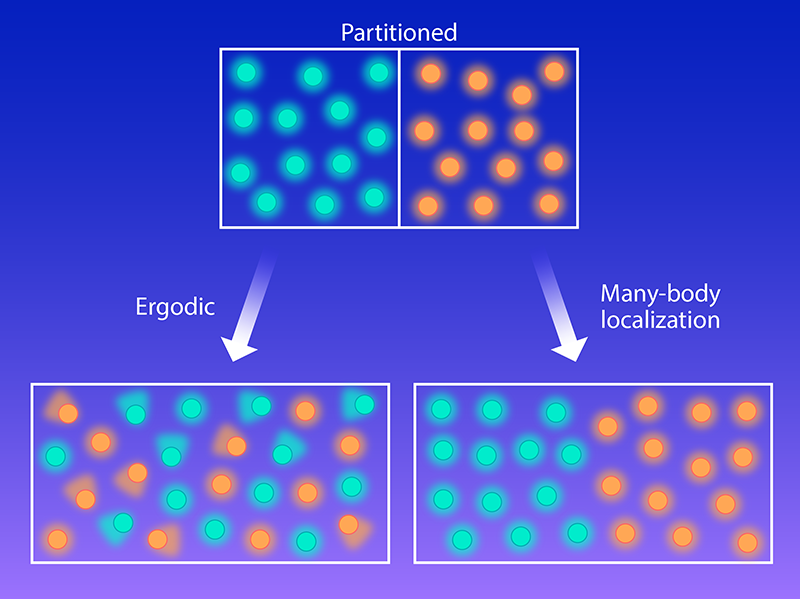
In 1958, physicist Philip Anderson showed that in a sufficiently disordered potential landscape, a single quantum particle, such as an electron, becomes spatially localized within a small region in the vicinity of its initial position [2]. What about multiple particles in the same potential landscape? Conceivably, they can scatter off one another, yielding new pathways to escape localization. But if despite these pathways, the system remains spatially localized, it is said to exhibit many-body localization (MBL). MBL systems constitute a nonergodic phase of matter. They are perfect insulators at nonzero temperature.
Over the past 70 years, a growing body of theoretical work has shown that in one-dimensional systems, MBL is stable and resists thermalization. In higher dimensions, rare, large regions with low spatial disorder destabilize MBL. These regions behave as poor heat baths, with low specific heats and granularity in the heat that they can absorb. Nevertheless, they can become better heat baths by equilibrating localized degrees of freedom at their boundaries and absorbing them. Only in one dimension can this runaway process (dubbed a quantum avalanche) be stopped, allowing for the possibility of stable MBL.
Attempts to empirically confirm MBL and the broader dynamical phase diagram of disordered quantum systems have been beset by controversy. Quantum simulators can mimic the idealized dynamical experiment of letting particles go in a disordered potential and watching what happens, but they are limited to relatively short times. These experiments observe an MBL-like regime in all dimensions. By contrast, numerically exact studies are restricted not by time but to small numbers of particles (around ten particles across 20 sites). The results they yield are inconsistent with a simple theoretical picture of two phases: an MBL phase at strong disorder and an ergodic phase at weak disorder. Subsequently, dissenting opinions have emerged. In 2020 Jan Šuntajs of the Jožef Stefan Institute, Slovenia, and his collaborators argued that the MBL phase does not exist; in sufficiently large systems, particles always spatially delocalize [3].
Morningstar and his colleagues elucidated how empirical findings can be squared with theory. They emphasized that the phase diagram has three regimes: an ergodic phase, an MBL phase (where even large systems remain nonergodic), and, significantly, an intervening “MBL regime” (where accessible systems are nonergodic, but sufficiently large systems are ergodic). Numerical simulations probed the crossover from the ergodic regime to the MBL regime. At this crossover, numerical systems are just too small to host the poor baths that seed quantum avalanches. Instead, the crossover is determined by entirely distinct physics—the proliferation of many-body resonances [4, 5]. Loosely speaking, in a many-body resonance, multiple particles spread over multiple sites flip-flop between two configurations. Resonances unstick the particles and can cause delocalization. In the crossover region, the probability to form a resonance atop a localized configuration of particles changes dramatically, from being a rare event in the MBL regime to being common at all length scales in the ergodic phase.
If numerical systems are too small to host poor baths, how can one probe the crossover to the true MBL phase? The key technical innovation devised by Morningstar, in conjunction with Dries Sels [6] of New York University, is recasting the criterion for quantum avalanches: if, when connected to a perfect bath, the equilibration time of a localized chunk of system is too long, then it is not possible for a poor bath to trigger the equilibrating avalanche. Importantly, this perfect bath equilibration time is numerically measurable and provides a lower bound on the disorder strength necessary for the MBL phase. Morningstar and Sels found that the MBL phase requires much larger disorder strengths than previously anticipated: at least 7 times the strength at which the MBL regime develops in numerically studied models.
As the relevant timescales are exponentially sensitive to the disorder strength, the researchers’ results suggest that the MBL phase is physically inaccessible. In ultracold atomic experiments that probe MBL [7], for example, the dynamics of the MBL phase and the MBL regime become distinct only after approximately 1018 seconds. More than double the age of the Universe!
The work of Morningstar and colleagues and others has resolved several puzzles about the dynamical phase diagram of disordered systems. Looking ahead, the characterization of the physically accessible MBL regime is paramount. One question regards its dynamical signatures. For large sizes, recent work predicts a large hierarchy of timescales for different microscopic configurations to reach local thermal equilibrium. This property is reminiscent of classical glasses, so exploring the precise connection between such glasses and MBL is an exciting front.
Another application is to optimization problems. Solutions to these problems can be recast as searches for the ground states of disordered systems of many particles. Heuristic quantum algorithms that seek such ground states may go through the MBL regime before finding them. In the MBL regime, the system tunnels between resonant configurations; whether access to these resonances make the heuristic quantum algorithms faster than their classical counterparts remains to be seen.
References
- A. Morningstar et al., “Avalanches and many-body resonances in many-body localized systems,” Phys. Rev. B 105, 174205 (2022).
- P. W. Anderson, Local Moments and Localized States, Nobel Lecture, Nobel Prize in Physics (1977).
- J. Šuntajs et al., “Quantum chaos challenges many-body localization,” Phys. Rev. E 102, 062144 (2020).
- B. Villalonga and B. K. Clark, “Characterizing the many-body localization transition through correlations,” arXiv:2007.06586.
- P. J. D. Crowley and A. Chandran, “A constructive theory of the numerically accessible many-body localized to thermal crossover,” SciPost Phys. 12, 201 (2022).
- D. Sels, “Bath-induced delocalization in interacting disordered spin chains,” Phys. Rev. B 106, L020202 (2022).
- J.-Y. Choi et al., “Exploring the many-body localization transition in two dimensions,” Science 352, 1547 (2016).