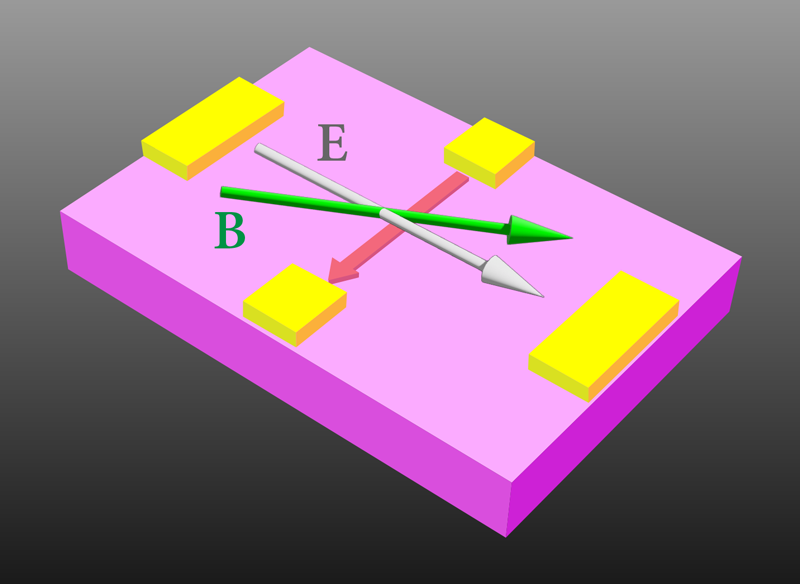
A New Hall Effect from Quantum Geometry
Throughout many branches of physics, a connection can be drawn between geometry and dynamics. In general relativity, for example, the motion of stars and planets is governed by the geometry of spacetime. In condensed matter, the motion of electrons in solids is influenced by the so-called quantum geometry, which describes how the electronic wave function evolves in momentum space. The quantum geometry can explain a wide range of observed phenomena, such as topological phases and quantum Hall effects, but it can also lead researchers to new electromagnetic responses. Guided by quantum-geometry predictions, Lujunyu Wang from Peking University and colleagues present experimental evidence of a new Hall effect, the magneto-nonlinear Hall effect, which is proportional to both an in-plane electric field and an in-plane magnetic field [1] (Fig. 1). The effect, which was isolated in a magnet with triangular symmetry, offers a new way to probe in the quantum geometry of materials.
Quantum geometry is a representation of the phase of the Bloch wave functions, which describe electronic behavior in a periodic potential. In the case of a two-level system, this phase can be represented by a unit vector in the momentum space of the electrons. In certain materials, this vector rotates as the momentum changes, an effect that can be characterized by two fundamental geometrical properties: the “quantum metric” and the “Berry curvature.” These two aspects of quantum geometry can describe many phenomena including surface currents in topological insulator and anomalous Hall effects in which the transverse Hall current occurs in the absence of an external magnetic field.
Recently, researchers have uncovered a connection between quantum geometry and nonlinear electromagnetic effects [2–10]. Here, the nonlinearity is a higher-order response to the input electromagnetic fields. Nonlinear electrical transport is the foundation of applications such as rectification and wave mixing. Classically, the most well-known nonlinear device is a p-n junction. In quantum materials, nonlinear transport suggests novel device applications but also provides a powerful probe of the quantum geometry of the conduction electrons.
One example of these nonlinear responses is the electrical nonlinear Hall effect, characterizing a Hall current that scales as the square of the applied electric field [5, 6]. This phenomenon can be induced by localized patterns in the quantum geometry, where the Berry curvature (or the quantum metric) is globally zero but has positive and negative dipole-like regions in momentum space. The electrical nonlinear Hall effect has sparked considerable interest, having been observed recently in two-dimensioanl WTe2[7, 8], in MnBi2Te4 heterostructures [9, 10], and in other noncentrosymmetric systems.
Theorists have predicted a similar nonlinear response called the magneto-nonlinear Hall effect, which describes a Hall current that depends both on the applied electric and magnetic fields. This effect also has a geometrical origin: the magnetic field induces a Berry curvature in the material, and this curvature generates a Hall current that is transverse to the electric field. Although the phenomenon was proposed about a decade ago [6], its experimental observation has remained elusive.
Theoretically, the magneto-nonlinear Hall effect can occur either when the magnetic field is perpendicular to the surface over which the electric field is applied or when the two fields are in the same plane. However, an out-of-plane magnetic field would result in a substantial classical Hall effect, overwhelming the magneto-nonlinear Hall signal. Therefore, the best chance of seeing the effect is to apply an in-plane magnetic field. In this case, the difficulty is that the material must break rotational symmetry in order for a signal to show up.
To overcome these challenges, Wang and colleagues identified the kagome magnet Fe3Sn2 as an ideal material platform for searching for this new effect. In the case of Fe3Sn2, its in-plane magnetization breaks the threefold rotational symmetry. In addition, the material’s band structure—with its topological Weyl points near the Fermi level—can significantly enhance the quantum-geometrical effects.
To look for the nonlinear effect, the researchers performed systematic Hall measurements, finding a transverse current that depended on the applied electric and magnetic fields. Crucially, they demonstrated that the observed signal is indeed antisymmetric with respect to the magnetic field, as expected for a true Hall effect. Furthermore, the researchers investigated how the Hall signal varied as they rotated the in-plane magnetic field relative to the electric field. They found a 2𝜋∕3 cyclical pattern consistent with the symmetry of the Fe3Sn2 crystal. This alignment is significant, as intrinsic nonlinear responses must reflect the crystalline symmetry of the material, distinguishing them from trivial nonlinear responses stemming from Joule heating or contact asymmetry. The researchers further explored temperature dependence, noting that the magneto-nonlinear Hall signal diminishes rapidly with increasing temperature, a behavior distinct from the ordinary Hall effect. Through these systematic experimental observations, the team was able to confirm that the observed signal came from the magneto-nonlinear Hall effect.
To probe the geometry of this new effect, the researchers performed a careful theoretical analysis. They discovered that the Weyl points of Fe3Sn2 function as “hot spots” for a type of geometric property called the anomalous orbital polarizability. Similar to the diode pattern in the electrical nonlinear Hall effect, the anomalous orbital polarizability is the driving force behind the magneto-nonlinear Hall effect. Importantly, the magnitude of the calculated nonlinear Hall conductivity aligns closely with the experimental data.
The new findings by Wang and co-workers provide inspiration for intriguing new directions and hold significant implications for Hall effect studies. The discovery should spark interest in future explorations of the magneto-nonlinear Hall effect in other quantum materials. As mentioned above, this effect requires the absence of rotational symmetry, making it potentially observable in monoclinic or triclinic lattices like Td-WTe2 and MoTe2. Moreover, the magneto-nonlinear Hall effect can serve as a probe for spontaneous rotational symmetry breaking, a phenomenon that can occur through nematic ordering in correlated systems such as iron-based superconductors and magic-angle twisted bilayer graphene systems.
Another possible future direction is in the study of materials with optical probes. Here, light would be reflected off a material with an applied in-plane magnetic field. A similar type of nonlinear response in the material could induce a change in the light’s polarization—either a Kerr rotation or circular dichroism. Consequently, one can contemplate broadening the scope of quantum-geometry investigations to include nonmagnetic semiconductors and insulators.
Lastly, this finding reports a Hall effect induced by an in-plane magnetic field. Many previous experiments observed the so-called planar Hall effect, which is induced by in-plane magnetic-field anisotropy, making it symmetric with respect to the magnetic field. As mentioned, a true Hall effect is antisymmetric, in close relation to its dissipationless and topological properties. Therefore, these results clearly open a new chapter in the study of Hall effects.
Correction (15 March 2024): The original text implied the result represents the first instance of a Hall effect induced by an in-plane magnetic field. The text was corrected to reflect the fact that similar behavior was observed in Fe3Sn2, as reported in an arXiv preprint .
References
- L. Wang et al., “Orbital magneto-nonlinear anomalous Hall effect in kagome magnet Fe3Sn2,” Phys. Rev. Lett. 132, 106601 (2024).
- J. Orenstein et al., “Topology and symmetry of quantum materials via nonlinear optical responses,” Annu. Rev. Condens. Matter Phys. 12, 247 (2021).
- Y. Tokura and N. Nagaosa, “Nonreciprocal responses from non-centrosymmetric quantum materials,” Nat. Commun. 9, 3740 (2018).
- Q. Ma et al., “Topology and geometry under the nonlinear electromagnetic spotlight,” Nat. Mater. 20, 1601 (2021).
- I. Sodemann and L. Fu, “Quantum nonlinear Hall effect induced by Berry curvature dipole in time-reversal invariant materials,” Phys. Rev. Lett. 115, 216806 (2015).
- Y. Gao et al., “Field induced positional shift of Bloch electrons and its dynamical implications,” Phys. Rev. Lett. 112, 166601 (2014).
- K. Kang et al., “Nonlinear anomalous Hall effect in few-layer WTe2,” Nat. Mater. 18, 324 (2019).
- Q. Ma et al., “Observation of the nonlinear Hall effect under time-reversal-symmetric conditions,” Nature 565, 337 (2018).
- A. Gao et al., “Quantum metric nonlinear Hall effect in a topological antiferromagnetic heterostructure,” Science 381, 181 (2023).
- N. Wang et al., “Quantum-metric-induced nonlinear transport in a topological antiferromagnet,” Nature 621, 487 (2023).