Altermagnetism Then and Now
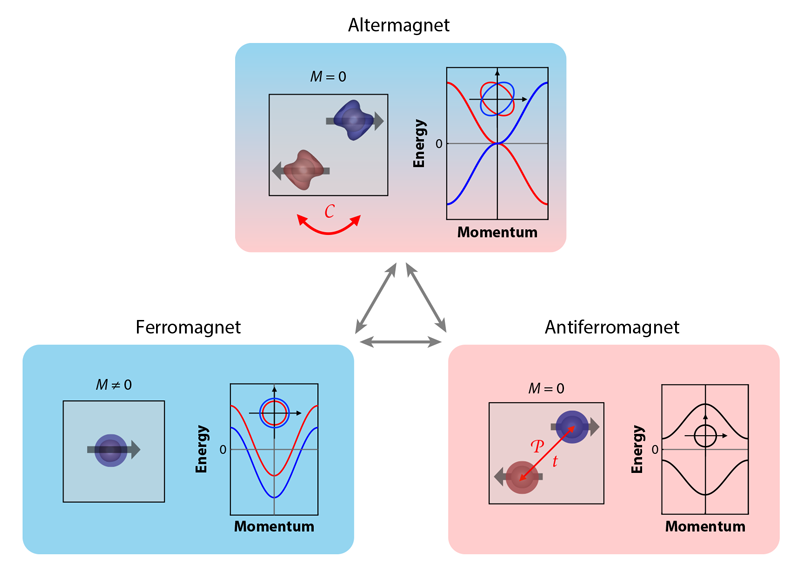
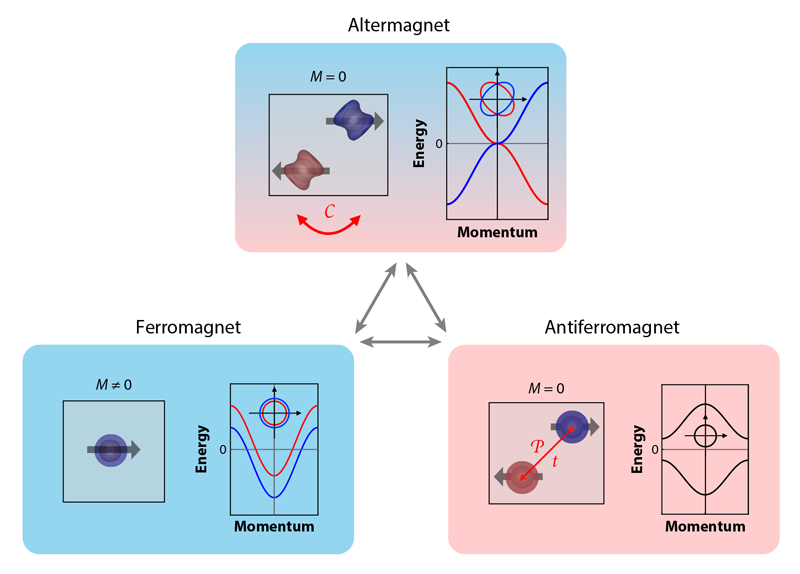
Collinear magnetism, where magnetic moments of all ions are parallel or antiparallel to each other, is a century-old concept in condensed-matter physics. In the past two decades, researchers began exploring the exotic world of noncollinear magnets, which include spin spirals, skyrmions, spin ices, and more. But more recently a fundamentally new form of collinear magnetism has emerged: altermagnetism. Like ferromagnetism, it breaks time-reversal symmetry and harbors anomalous transport properties, such as the anomalous Hall effect and magneto-optics. Like antiferromagnetism, it has, by symmetry, no net magnetization. The phenomenon was identified between 2019 and 2021 by four different groups [1–4]. In 2022, Libor Šmejkal of Johannes Gutenberg University Mainz in Germany and colleagues named it altermagnetism [5]. Despite its youth, altermagnetism is already proving a fertile field for theory and for proposed applications. Meanwhile, experimenters are closing in on confirming the theorists’ predictions.
Altermagnetism is the culmination of a series of previous conceptual leaps. Among them was the realization that a dark mineral called lodestone, or magnetite, whose natural magnetic properties were known since ancient times, is a collection of aligned individual microscopic magnets. As the theory of ferromagnetism—as the phenomenon became to be called—developed, two other important conceptual realizations took place. First, it turned out that the oldest known magnetic material, magnetite (Fe3O4), was not exactly what people initially had thought ferromagnets were. Rather than all the Fe ions being aligned, two thirds of them have parallel magnetic moments, while one third have antiparallel ones. In 1948 Louis Néel called this arrangement ferrimagnetism. But even then, it was quite clear that there was no physical difference between ferro- and ferrimagnets, the former just being a specific case of the latter. In principle one can imagine a situation where the two (or more) magnetic subsystems that are different by symmetry or chemistry exactly compensate each other. Microscopically, such “spin-compensated” materials are indistinguishable from ferromagnets, even though macroscopically they are not magnetic. Moreover, on a nonrelativistic level the compensation may be exact, and protected, albeit not by crystal symmetries.
Néel also realized that another class of magnetic materials must exist, one fundamentally different from ferrimagnets by symmetry. He assumed a perfect crystal lattice of magnetic ions whose magnetic moments (spins) are fully collinear, but every other spin is flipped. Such a material is partitioned into two sublattices, related by a lattice translation. That is to say, when we apply a time-reversal operation, which results in flipping all spins, the resulting magnetic landscape differs from the original one only by a uniform translation. Given that the Schrödinger equation is invariant under translation, the electron spectrum is manifestly identical for the two spin directions and the net magnetization of the crystal is exactly zero. These are so-called Néel antiferromagnets.
At this point, standard textbooks on condensed-matter physics usually stop discussing magnetism. Practitioners of the art, however, have known for quite some time about variants of antiferromagnetism. For instance, if there is an even number of symmetry-equivalent magnetic ions within the same unit cell, one can imagine an antiferromagnet in which half of such ions have one spin direction and half the opposite. The two spin sublattices remain connected by a symmetry operation, and this operation is not a translation but a rotation, a reflection, a screw, and so on. One can prove that if these symmetry operations include a spatial inversion, the electron spectra are unaffected, and such antiferromagnets, for all intents and purposes, are the same as textbook Néel antiferromagnets. Researchers have found many examples of these so-called “zero q antiferromagnets.”
But there is an exciting possibility of yet another class of materials. Although formally antiferromagnets (spin-compensated by symmetry), they are qualitatively different: mapping of one spin sublattice onto the other is performed by a symmetry operation that is neither translation nor inversion. Since such operations do not preserve electronic spectra, they will be different: their bands will be split in two by spin. This possibility—the animating idea of altermagnetism—was identified only around 2019 by four groups [1–4]. They called this phenomenon different names, but the one that has gained currency was proposed by Šmejkal and colleagues [5]: altermagnetism.
In the past few years researchers realized that whereas altermagnets share some of their key properties with antiferromagnets (most importantly, magnetic moments on different ions compensate each other by symmetry), they also share even more with ferromagnets (the possibility of anomalous Hall effect, magneto-optical response, tunneling magnetoresistance (TMR), and other phenomena [6]). In this sense, altermagnets are rather similar to another class of magnetic materials—fully compensated ferrimagnets—sporadically discussed in earlier literature. In the latter case, we speak of materials that have two (or more) opposite-spin sublattices, which are not related by any crystal symmetry. It seems, at first glance, that such ferrimagnets will never be exactly compensated: a difference of two numbers that no symmetry requires to be the same can be small but never exactly zero. This is, however, not the case if the material in question in an insulator or a half metal (an insulator in one spin channel but not both). By Quin Luttinger’s theorem, such a material can have only an integer (per unit cell) spin magnetic moment (in Bohr magnetons). Because of that requirement, the moment may be exactly zero, 1, or 2 but never a small nonzero number. Thus, if the electron structure is such that the net magnetization must be small, it will be exactly zero. Such cases had been reported before and became known as Luttinger-compensated ferrimagnets [7].
Theorists have already explored numerous ramifications of altermagnets and Luttinger ferromagnets for spintronics [5, 7] and superconductivity [8]. But there are other potential applications, especially in TMR, a workhorse of modern computer-memory devices. Indeed, current TMR devices, based on ferromagnetic materials, are limited in their speed to gigahertz frequencies by the ferromagnetic resonance—that is, the coupling between magnetization and an electromagnetic wave. Altermagnets and Luttinger ferromagnets have resonance frequencies that are 3 orders of magnitude higher. Altermagnetic devices are also appealing for potential applications in spintronics and neuromorphic information technologies, owing to the predicted giant spin-current ratio signals [5]. Other prospects for applications are in low-dissipation nanoelectronics, which rely on altermagnets’ unconventional anomalous Hall currents and topological quasiparticles [1, 4, 5].
At present, the case that a real material exhibits all the predicted features of altermagnetism remains to be clinched. In particular, one challenge to both laboratory detection and practical application is creating samples of altermagnets and Luttinger ferromagnets that have a single magnetic domain. That’s because most effects of interest will cancel each other if there’s more than one domain. A single-domain sample would also be lower in energy than a multidomain one. On the other hand, if domains have already formed kinetically, it is hard to exhort a force onto domain walls. This material challenge needs to be addressed soon.
Acknowledgments
Igor Mazin acknowledges conversations with Jairo Sinova and Libor Smejkal and funding from ARO under Cooperative Agreement No. W911NF-22-2-0173.
References
- L. Šmejkal et al., “Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets,” Sci. Adv. 6 (2020).
- S. Hayami et al., “Momentum-dependent spin splitting by collinear antiferromagnetic ordering,” J. Phys. Soc. Jpn. 88, 123702 (2019).
- L. D. Yuan et al., “Giant momentum-dependent spin splitting in centrosymmetric low-Z antiferromagnets,” Phys. Rev. B 102, 014422 (2020).
- I. I. Mazin et al., “Prediction of unconventional magnetism in doped FeSb2,” Proc. Natl. Acad. Sci. U.S.A. 118 (2021).
- L. Šmejkal et al., “Emerging research landscape of altermagnetism,” Phys. Rev. X 12, 040501 (2022).
- L. Šmejkal et al., “Beyond conventional ferromagnetism and antiferromagnetism: A phase with nonrelativistic spin and crystal rotation symmetry,” Phys. Rev. X 12, 031042 (2022).
- I. Mazin and The PRX Editors, “Editorial: Altermagnetism—A new punch line of fundamental magnetism,” Phys. Rev. X 12, 040002 (2022).
- I. I. Mazin, “Notes on altermagnetism and superconductivity,” arXiv:2203.05000.