Exploring the Black Hole Population with an Open Mind
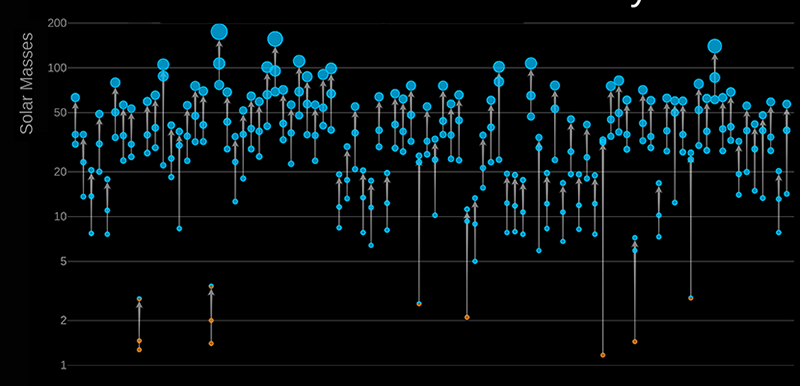
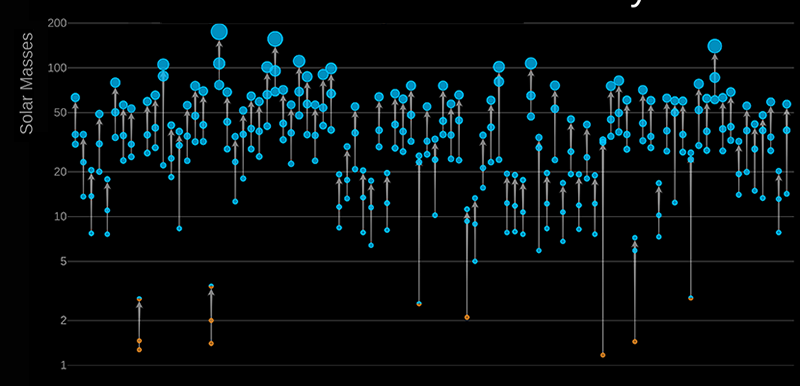
Since the first groundbreaking observation of gravitational waves from a black hole merger [1], a worldwide network of observatories–LIGO, Virgo, and KAGRA—has discovered nearly a hundred mergers involving black holes and neutron stars (Fig. 1). The nature of this population of compact objects has implications for nearly every aspect of astrophysics and cosmology. However, understanding how gravitational-wave sources fit into our astrophysical theories has proved challenging. Many of the discoveries have confirmed our expectations, but some—such as those of asymmetric black hole binaries or of unexpectedly massive black holes—defy them. How can we understand new observations in the context of existing knowledge while remaining open to surprises that challenge our understanding? Thomas Callister of the University of Chicago and Will Farr of Stony Brook University, New York, offer a solution to this question: a “parameter-free” model for describing the black hole binary population [2]. Unlike most present-day models, their approach describes this population in an “agnostic” way—without assuming that the black hole masses, spins, and redshifts follow parametrized mathematical distributions derived from theoretical predictions. As such, the new model may enable the discovery of truly unexpected features of the black hole population.
Gravitational waves give us unprecedented insight into the life and death of stars, allowing access to some of the youngest, faintest galaxies in the Universe. They have revealed a population of black holes with masses between a few and 150 times the mass of the Sun. These black holes are likely skeletons left over by the deaths of the Universe’s most massive stars in relatively chemically pristine (“low-metallicity”) pockets of the Universe [3]. These environments cannot be accessed with traditional astronomy observations, which typically probe big, chemically rich galaxies that have undergone periods of extensive star formation.
The masses, spins, and redshifts of black hole binaries encode information about how, where, and when the binaries were made. For example, “pileups” and “gaps” in the black hole mass distribution can be interpreted as resulting from exotic phenomena such as pulsational pair-instability supernovae [4, 5]. The distribution of black hole spin orientations can be used to distinguish between scenarios in which two black holes spend their whole lives in a binary system and those in which they exchange companions multiple times before merging [6]. The redshift dependence of the merger rate probes how star formation varies across cosmic time and how long it takes for black holes to merge after the birth of their progenitor stars [7]. In these examples, the task might seem simple: extract physical insight by fitting the binary black hole mass, spin, and redshift distributions. In reality, this process is challenging because we lack complete, reliable first-principles models to analyze the data.
In the absence of these models, a common approach has been to fit the binary black hole population with simple, phenomenological models. Guided by theoretical predictions, gravitational-wave data analysts propose various features expected to describe the black hole population. They typically start by using a power law to describe the black hole mass distribution, because the mass distribution of the black holes’ stellar progenitors is often described as a power law. However, our understanding of supernovae suggests that the relationship between initial stellar mass and black hole mass is nonlinear. In particular, pulsational pair-instability supernovae should lead to a wide range of initial stellar masses collapsing to a narrow range of black hole masses. To account for this effect, the power law is usually combined with a Gaussian peak, whose location, height, and width are constrained by the data [5]. However, currently available data favor a Gaussian peak at lower masses than predicted from pair instability, casting doubts on the peak’s origin [8]. Should we then look for more Gaussian peaks? We could come up with countless combinations of power laws and Gaussians to throw at the data, but why stop at just power laws and Gaussians? Callister and Farr offer a natural solution through their flexible, nonparametric model.
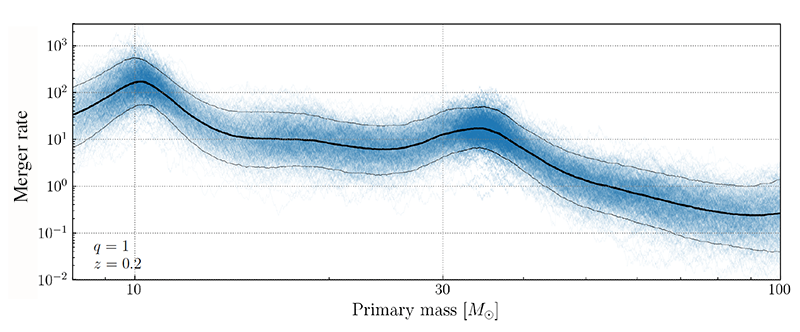
The model fits the binary black hole merger rate as a function of mass, spin, and redshift through a so-called autoregressive process. Compared with parametric models, the autoregressive model only assumes that the merger rate is a continuous function. It is also more flexible than previous models (such as those based on “splines” or on a “binned Gaussian process”) that are dubbed nonparametric but are based on underlying parametrized functions describing a priori black hole distributions. The new model’s freedom allows any variety of features—including peaks, dips, and breaks in the black hole property distributions—to be recovered from the data, without biases deriving from expectations about these features. However, the results from a parameter-free model are much more complex to interpret than those from a parametric one. The model’s output is simply a bunch of squiggly lines that are not inherently meaningful.
To tackle this problem, Callister and Farr introduce statistical techniques to extract meaningful features from their nonparametric inference (Fig. 2). Some of the extracted features—such as a peak in the primary black hole mass distribution at 35 solar masses—had previously been identified by a serendipitous choice of parameterized model. Other features confirm hints delivered by previous nonparametric approaches [8–10]. Such features include a second peak at 10 solar masses and a merger rate that increases more steeply for large redshifts (between 0.4 and 1) than for redshifts corresponding to the “local Universe” (between 0 and 0.4). This finding could imply a nontrivial evolution of black hole progenitors and of their merger times.
Callister and Farr don’t envision that their flexible, nonparametric model will entirely replace parametric ones, but they propose combining the two approaches in an iterative process. Nonparametric models could first be applied to pinpoint possible new features, which parametric models could characterize and interpret. The results could then be rechecked and refined using nonparametric models as more observations become available. Ultimately, the features extracted from such a process could be used to place constraints on the underlying astrophysics. This approach holds great promise for strengthening the link between observations and theoretical predictions.
LIGO-Virgo-KAGRA’s ongoing observing run is expected to triple the sample of binary black hole merger events, and the next decade might bring thousands, if not millions, of binary black hole detections. At the same time, our theoretical models will improve as we better understand the physical processes behind the Universe’s production of binary black holes. With these prospects, we should stay open minded to surprises, and flexible models such as that proposed by Callister and Farr will help us explore “unknown unknowns” that might otherwise be missed.
References
- B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Observation of gravitational waves from a binary black hole merger,” Phys. Rev. Lett. 116, 061102 (2016).
- T. A. Callister and W. M. Farr, “Parameter-free tour of the binary black hole population,” Phys. Rev. X 14, 021005 (2024).
- A. Heger et al., “Black holes as the end state of stellar evolution: Theory and simulations,” The Encyclopedia of Cosmology (2023).
- M. Fishbach and D. E. Holz, “Where are LIGO’s big black holes?” Astrophys. J. Lett. 851 (2017).
- C. Talbot and E. Thrane, “Measuring the binary black hole mass spectrum with an astrophysically motivated parameterization,” Astrophys. J. Lett. 856 (2018).
- S. Vitale et al., “Use of gravitational waves to probe the formation channels of compact binaries,” Class. Quantum Grav. 34 (2017).
- M. Chruślińska, “Chemical evolution of the Universe and its consequences for gravitational‐wave astrophysics,” Ann. Phys. 536 (2022).
- R. Abbott et al. (LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration), “Population of merging compact binaries inferred using gravitational waves through GWTC-3,” Phys. Rev. X 13 (2023).
- A. M. Farah et al., “Things that might go bump in the night: Assessing structure in the binary black hole mass spectrum,” Astrophys. J. Lett. 955 (2023).
- B. Edelman et al., “Cover your basis: Comprehensive data-driven characterization of the binary black hole population,” Astrophys. J. Lett. 946 (2023).