The Universe’s Topology May Not Be Simple
Is the Universe simply connected like a sphere or does it contain holes like a doughnut or a more complicated structure? The topology of the Universe—that is, its overall geometry—remains far from settled, according to a collaboration of cosmologists. Despite past claims that observations of the cosmic microwave background (CMB) rule out various topologies, the researchers contend that many of these shapes, including some strange ones, have not been contradicted by the evidence [1].
The overall geometry of the Universe is thought to have been determined by quantum processes that unfolded in the initial moment of the big bang. Identifying the topology of the Universe would provide researchers with an important clue as to the nature of those quantum processes and could help them sift through the many proposed theories of the early Universe.
A given topology describes the connectedness of spacetime. Among the nontrivial topologies that the Universe could conceivably possess is the 3-torus. To picture one, imagine distorting a cube by bending a pair of opposite sides around until they face each other and then gluing them together. Then imagine the same for the other two pairs. A line of sight from the center of the cube that previously went out to infinity would now return to the cube’s center via a closed loop.
Closed loops also feature in other topologies that might describe the Universe, and they could lead to an optical illusion: the observation of the same part of the Universe in different parts of the sky. However, there are length scales associated with each topology—the diameter of a closed loop, for example—and if the length scales are too large, then multiple views of the same cosmic neighborhood might not be possible. The illusion might not appear because there may not have been enough time since the big bang for some of the light to reach us; in other words, the length scales may exceed the “CMB horizon,” the distance to the source of the oldest light we can see.
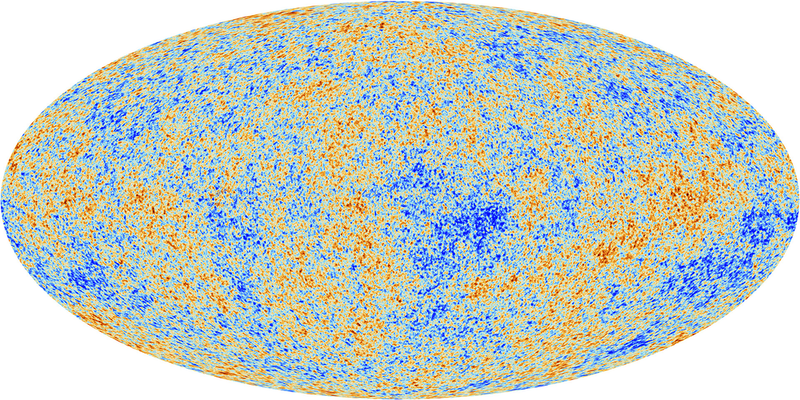
Full-sky maps of the CMB in recent decades have provided detailed views of the young Universe but no signs of repeating patterns (correlations) that might signal closed loops. The search for the topology of the Universe in the CMB appeared unpromising, if not over, as of a decade ago. However, last year an international group of cosmologists calling themselves the COMPACT Collaboration revived the quest. Now, in the first publication from COMPACT, the researchers show that certain exotic topologies are actually consistent with CMB observations and that, in fact, only a small fraction of possible topologies has been explored so far.
Rather than consider all 18 mathematically possible topologies of Euclidean (flat) space, the COMPACT Collaboration chose to focus on the 3-torus, called E1, and two of its extensions, E2 (a 180° twisted version of E1) and E3 (a 90° twisted version of E1). Their reasoning: if even these relatively simple topologies are not ruled out, other more complicated ones are also likely to remain contenders.
According to the collaboration’s calculations, the 3-torus E1 is ruled out by current observations if its characteristic scale is smaller than the CMB horizon, as expected. But it turned out that E2 and E3 remain in play even if their scales are much shorter than the CMB horizon. That’s because their connectedness involves twists. A region of the Universe viewed though a twisted closed loop would produce two views of itself that would be different but would remain correlated. Determining whether those correlations yield a detectable topological fingerprint in the CMB is next on the collaboration’s agenda.
Cosmologist Oliver Philcox of Columbia University agrees that the topology of the Universe remains an open question. “There’s a lot of possible ways the Universe could be topologically connected, and it’s hard to rule them out,” he says.
–Charles Day
Charles Day is a Senior Editor for Physics Magazine.
References
- Y. Akrami et al. (COMPACT Collaboration), “Promise of future searches for cosmic topology,” Phys. Rev. Lett. 132, 171501 (2024).