How to Charge Up a Sliding Water Drop
A liquid drop sliding down an inclined surface can become electrically charged, but only if the surface is hydrophobic (water repelling). Now researchers have developed an analytical model that makes quantitative predictions for the process and that explains why a hydrophobic surface is necessary [1]. The model, validated with experiments, shows that the large contact angle between the liquid surface and a hydrophobic solid surface has a strong effect on the charge at the drop edge. The theory may help researchers better understand a wide range of processes, such as the undesirable charging of semiconductor wafers when they are rinsed during manufacturing and the desirable build up of charge in the process of energy harvesting from water drops.
Charge separation between two solids is familiar to us from situations where materials rub against each other, such as clothing fabrics or a balloon and human hair. About three decades ago, researchers discovered that a water drop moving over a hydrophobic, electrically insulating surface also generates electric charge [2]. Since then, others have found this process to be important in, for example, the shedding of rainwater by plant leaves and the scheme for harvesting electricity by collecting condensed water drops [3].
The charging occurs when chemical reactions between the solid and the water release protons into the water and leave negative charges behind on the solid surface. But despite some previous theoretical work, there has not been a complete drop-charging theory that makes testable predictions and that explains the requirement of a hydrophobic surface.
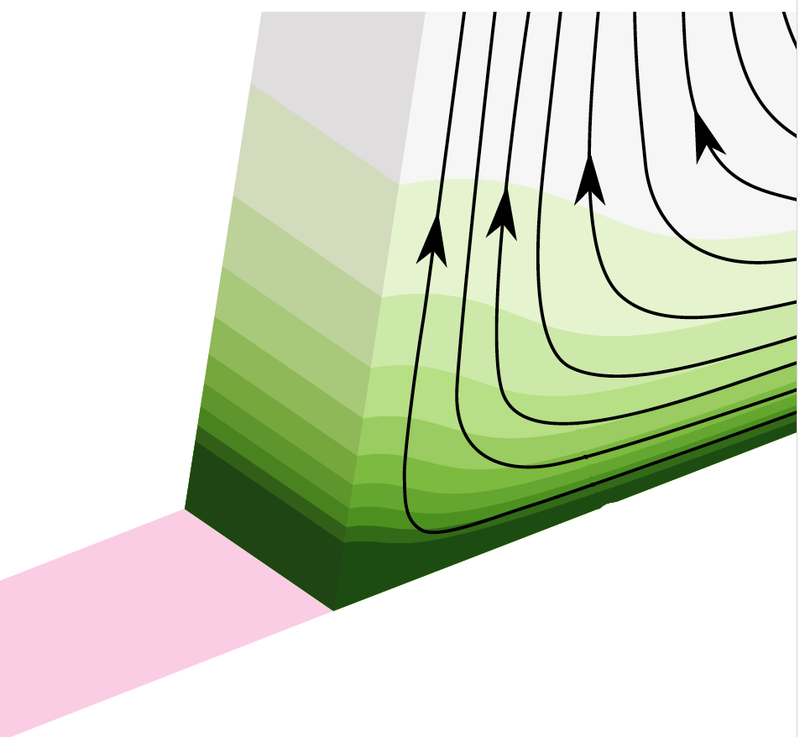
To develop their theory, Steffen Hardt of the Technical University of Darmstadt in Germany and his colleagues zoomed in on the liquid–solid interface, with a negatively charged surface below and positively charged protons in the fluid above. They focused on three main effects that together determine the amount of positive charge that the drop accumulates. First, there’s a two-way chemical reaction that continually creates and removes charges at the interface. Second, the contact angle that the liquid surface makes with the solid surface at the drop edges determines the space available for protons at the edges of the interface, which in turn affects the electric field. And finally, as the rear edge of the drop arrives over a patch of the surface, it deflects the fluid upward, which moves protons upward and distorts the electric field.
The theory predicts that with increasing drop speeds, this last effect should lead to reduced electric fields at the edges and therefore reduced charging of drops. It also predicts that charge should increase with contact angle, which is determined by the hydrophobicity of the surface. (Hydrophobic surfaces like plastics, where water is more likely to form “beads,” have larger contact angles than water-loving, or hydrophilic, surfaces like glass.) These predictions were borne out by the team’s simulations.
To further test the predictions, the researchers performed an experiment where a drop of water becomes charged as it moves down an inclined surface, and the speed is controlled by the inclination angle. The drop then comes into contact with an electrode and discharges. The data showed that the charge decreased with increasing speed according to a relationship that was in good agreement with the theory. This last result may appear surprising, says Darmstadt team member Aaron Ratschow. “This is unexpected because other contact electrification mechanisms, like solid–solid electrification, increase at higher velocities.”
Ratschow says that the team’s theory will help researchers understand charging in many situations. “This [model] has implications for self-cleaning surfaces, where drops are supposed to run off easily, as well as [for] coating and printing applications, where drops should stick and spread,” he says. In addition, in semiconductor manufacturing, wafers can become charged because they must be rinsed many times with ultrapure water, and the resulting voltages—which may be on the order of kilovolts—can damage them.
“The analytical model fits well with the experimental data for small droplet velocities,” but it has some limitations, says Lars Egil Helseth, who studies electromagnetic fields and microstructures at the University of Bergen in Norway. He says the model can be a useful starting point for more realistic theories that may include more chemistry details and a wider range of cases, such as drops traveling at larger velocities and drops sliding on surfaces that produce smaller contact angles.
–Elizabeth Fernandez
Elizabeth Fernandez is a freelance science writer based in Raleigh, North Carolina.
References
- A. D. Ratschow et al., “How charges separate when surfaces are dewetted,” Phys. Rev. Lett. 132, 224002 (2024).
- K. Yatsuzuka et al., “Electrification phenomena of pure water droplets dripping and sliding on a polymer surface,” J. Electrost. 32, 157 (1994).
- Y. Sun et al., “Using the gravitational energy of water to generate power by separation of charge at interfaces,” Chem. Sci. 6, 3347 (2015).