Getting a handle on spin

Matthew F. Doty; Daniel Gammon

Viewpoint

Getting a handle on spin

Matthew F. Doty

Dept. of Materials Science and Engineering, University of Delaware, Newark, DE 19716

Daniel Gammon

Naval Research Laboratory, Washington, DC 20375, USA

February 23, 2009• Physics 2, 16

Two theoretical studies reveal how one might achieve electric-field control of spin in semiconductors, both in an impurity-localized electron, and also with a quantum dot molecule.

Figure caption — **Figure 1:** The spin projection of a single hole in a quantum dot molecule has an anisotropic $g$ factor that is highly sensitive to electric field. As a result, a modulated electric field from a local gate electrode in the presence of a static magnetic field could be used to rotate the spin—a technique called $g$ -tensor modulation resonance. Moreover, light with a frequency that is resonant with the molecule’s optical transition could be used to initialize the spin and also to measure it after rotation. Thus one approach to quantum control of the spin would be (a) spin initialization through optical pumping, (b) coherent spin control through $g$ -tensor modulation, (c) spin measurement through optical cycling techniques.

The spin state of an electron serves as a quantum memory. A coherent superposition of up and down spin states lasts for a relatively long time, even in the fluctuating fields of the semiconductor environment. This long lifetime makes the electron spin attractive as a potential quantum bit (qubit), the fundamental unit of quantum information. Because quantum information processing has the potential to dramatically enhance computational speed for certain problems, there is tremendous interest in finding ways to control individual electron spins. Recent work by De et al. of the University of Iowa, reported in Physical Review Letters [1], and by Andlauer and Vogl of the Technical University in Munich, reported in Physical Review B [2], shows new ways in which spins can be controlled by electric fields rather than more complex methods.

The upside to using a localized spin as a qubit is that it is insulated from many environmental field fluctuations of the material. The downside is that this isolation makes it difficult to get control with external fields. Conventional electronics use only the charge of the electron, which can be easily controlled with electric fields. One might think that it would be straightforward to control spins through standard magnetic resonance techniques. In practice, however, it is extremely difficult to apply high-frequency magnetic fields to one electron spin of many because the magnetic field would have to be spatially restricted to a region of a few nanometers.

An alternate, elegant approach is to use a local electric field applied through a gate electrode to control the spin by modulating an anisotropic $g$ factor—a tensor, in general—that quantifies how spins in the host material interact with an applied magnetic field. The modulated electric field causes an effective oscillating magnetic field that can induce controlled spin rotation, much like magnetic resonance. This approach is called $g$ -tensor modulation resonance, or $g$ -TMR [3]. Thus the search is on to find, or engineer, localized electron systems with $g$ -factor anisotropy that can be controlled by electric fields.

One well-known system for localizing an electron in a semiconductor is the donor impurity—the classic example of a solid-state atom. If, for example, a $Si$ atom substitutes for $Ga$ in a $GaAs$ crystal, the $Si$ atom brings in one more electron than the $Ga$ it replaces, and forms a solid-state version of a hydrogen atom. This is classified as a shallow donor because the electron has a small binding energy of only about $6 meV$ , and, correspondingly, a large Bohr orbit of about $10 nm$ . Consequently, the shallow donor can be treated using effective mass theory, that is, the extra electron is treated as a particle with reduced effective mass (and with an effective $g$ factor).

This approach was taken by De et al. [1], who showed that the $g$ factor of electrons bound to hydrogenic impurities has a substantial dependence on applied electric and magnetic fields. The applied electric field changes the orbital character of the electron wave function and through the spin-orbit interaction modifies the $g$ factor. The authors show that the dependence of the $g$ -factor anisotropy on applied electric field makes $g$ -TMR possible in this system.

Andlauer and Vogl consider a different approach involving quantum dots. In self-assembled quantum dots, the electrons are localized in regions with different material compositions, and thus different band gaps. For example, when $InAs$ is deposited on $GaAs$ it self-assembles into little islands about $10 nm$ in size, in part to minimize strain energy caused by the lattice mismatch with the $GaAs$ substrate. These $InAs$ regions have a lower band gap than the $GaAs$ . The strong confinement in all three dimensions creates discrete energy levels just like the particle-in-a-box model of introductory quantum mechanics. Single electrons can be trapped in these discrete energy levels to localize single spins. The energy levels of quantum dots, and their response to external fields, can be customized through size, shape, and composition.

$InAs$ quantum dots grown by molecular-beam epitaxy also have highly asymmetric $g$ factors and are promising for $g$ -TMR. However, in quantum dots it is not the electron that has the strongest $g$ -factor anisotropy, but the hole. A hole is the absence of an electron in an otherwise full semiconductor valence band and can be treated like a positively charged particle. A hole can be created by optically exciting a single electron from the valence band to the conduction band, leaving behind the hole. Alternatively, a static electric field can be applied to the quantum dot such that a single electron tunnels out to the substrate, again leaving behind the hole. Because holes are in the valence band, which is derived from atomic states with $p$ -like symmetry, holes have a much larger built-in spin-orbit character than electrons in the conduction band. In addition, some types of quantum dots are naturally asymmetric: the confinement is stronger along the growth axis than along the other two axes. The spin-orbit interaction and natural asymmetry combine to give holes in quantum dots much larger $g$ -factor anisotropy than electrons.

The response of quantum dots to an electric field can be greatly enhanced by forming quantum dot molecules: two $InAs$ quantum dots are stacked on top of each other, separated by a $GaAs$ barrier a few nanometers thick. The pair of dots can be controlled by applied voltage such that they share a single hole [4]. Normally the hole energy levels of the two dots are much different (because of differences in structure), tunneling between dots is negligible, and the dot states are atomiclike. However, when the two dots are tuned by an applied electric field to have the same hole energy, resonant tunneling of the hole becomes significant, and the state of the hole becomes molecularlike. The two atomiclike states combine to form a molecular “bonding” orbital with enhanced wave function in the barrier, and a molecular “antibonding” orbital with suppressed amplitude in the barrier.

At small barrier thickness the “bonding” state is the lower energy state, but for hole tunneling this order reverses at barrier thicknesses larger than $3 nm$ —another unusual result of the hole’s strong spin-orbit character [5]. What makes the molecule especially interesting is that the $g$ factor changes dramatically when the electric field is tuned through this molecular resonance [4]. The amplitude of the wave function in the barrier has a strong impact on the net $g$ factor, at least in part because the sign of the hole’s $g$ factor in the $GaAs$ barrier is opposite to that in the $InAs$ quantum dots.

Andlauer and Vogl obtain good quantitative agreement with the previous experimental results on quantum dots. The experiment measured only the component of the $g$ factor with the magnetic field applied along the direction of the electric field (which is along the quantum dot stacking direction). However, using their microscopic model, Andlauer and Vogl go on to calculate the full $g$ tensor of the quantum dot molecule as a function of the electric field. They find a very large anisotropy of the $g$ factor as a function of applied electric field, especially when the applied magnetic field is perpendicular to an electric field applied along the growth direction.

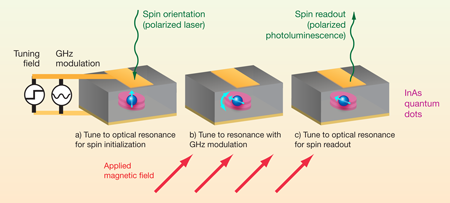
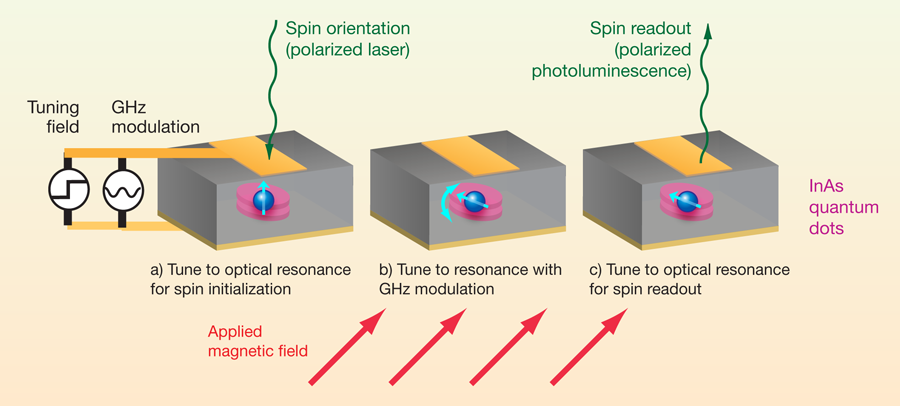
The quantum dot molecule has an anisotropic $g$ factor that is a highly nonlinear function of electric field and thus is ripe for $g$ -TMR. Andlauer and Vogl show that a vertical electric field combined with a static transverse magnetic field is sufficient to create all possible spin up and down superpositions. Such manipulations are critical for the implementation of quantum information processing. The results therefore show that quantum dot molecules are a promising material to use in confining and controlling single spins for quantum information processing. Figure 1 shows a schematic depiction of spin manipulation by $g$ -TMR in a single quantum dot molecule.

There are other promising methods to control a semiconductor spin qubit. For example, optical fields [6] and the hyperfine interaction with the underlying nuclear spin [7], among others, are being used. Of course, single qubit control is just one requirement of quantum information technology. It is also necessary in any given system to have methods for initialization, measurement, controlled entanglement of two spins, and error control. Each of these aspects has their own challenges and potential solutions. For example, the $InAs$ -based quantum dot system can rely on initialization based on optical pumping, and measurement based on optical cycling [8] in a manner similar to the quantum information approaches based on real atoms [9]. In the long run, however, scaling these single qubit systems and associated measurement techniques to large numbers of qubits will be the most difficult challenge. For any solid-state system this suggests that materials science and engineering will ultimately be the rate limiting step—especially in view of the limited support for advanced materials development [10].

References

A. De, C. E. Pryor, and M. E. Flatté, Phys. Rev. Lett. 102, 017603 (2009)
T. Andlauer and P. Vogl, Phys. Rev. B 79, 045307 (2009)
Y. Kato, R. C. Myers, D. C. Driscoll, A. C. Gossard, J. Levy, and D. D. Awschalom, Science 299, 1201 (2003)
M. F. Doty, M. Scheibner, I. V. Ponomarev, E. A. Stinaff, A. S. Bracker, V. L. Korenev, T. L. Reinecke, and D. Gammon, Phys. Rev. Lett. 97, 197202 (2006)
M. F. Doty, J. I. Climente, M. Korkusinski, M. Scheibner, A. S. Bracker, P. Hawrylak, and D. Gammon, Phys. Rev. Lett. 102, 047401 (2009)
D. Press, T. D. Ladd, B. Zhang, and Y. Yamamoto, Nature 456, 218 (2008)
J. R. Petta et al., Science 309, 2180 (2005)
D. Kim, S. E. Economou, S. C. Badescu, M. Scheibner, A. S. Bracker, M. Bashkansky, T. L. Reinecke, and D. Gammon, Phys. Rev. Lett. 101, 236804 (2008)
C. Monroe, D. M. Meekhof, B. E. King, W. M. Itano, and D. J. Wineland, Phys. Rev. Lett. 75, 4714 (1995)
T. Feder, Phys. Today 60 (8),26 (2007)

About the Authors

Matthew Doty earned a B.S. in physics from The Pennsylvania State University. He completed his Ph.D. in 2004 in experimental condensed-matter physics at the University of California, Santa Barbara, under the supervision of Prof. Mark Sherwin. After three years as a National Research Council Research Associate at the Naval Research Laboratory, he joined the faculty of Materials Science and Engineering at the University of Delaware in 2007. Matt’s research is focused on understanding and controlling the unique properties of coupled quantum dots for applications including quantum information processing and photovoltaics.

Dan Gammon has been at the Naval Research Laboratory since receiving his Ph.D. in physics at the University of Michigan in 1987. His research interests are in the optical properties of semiconductor nanostructures with an emphasis on quantum information science. He is a Fellow of the American Physical Society and of the Optical Society of America.