Electronic refrigeration on the micron scale

Jason R. Petta

Viewpoint

Electronic refrigeration on the micron scale

Jason R. Petta

Department of Physics, Princeton University, Princeton, NJ 08544, USA

April 6, 2009• Physics 2, 27

A quantum dot refrigerator that cools an electron gas close to

100 mK

may allow experimentalists to better probe electron-electron interactions in quantum confined systems.

Figure caption — **Figure 1:** Electronic cooling of a two-dimensional electron gas. Electronic states in an isolated island of 2DEG are filled to the chemical potential $μ$ according to the Fermi-Dirac distribution. A quantum dot (not shown) is tunnel coupled to the right (left) side of the island and functions as an energy selective source (drain) of electrons. The quantum dot to the right of the island injects electrons into unoccupied states slightly below the chemical potential, while the quantum dot contacting the left side of the island removes electrons with energy slightly above the chemical potential. Transport of a single electron through the sample in this configuration removes $\sim k T$ of energy, cooling the 2DEG island.

A host of physical phenomena including the quantum Hall effect and the fractional quantum Hall effect are best observed in cryogenic environments [1]. While experiments at $4.2 K$ and $1.3 K$ are routine, achieving the $mK$ temperatures required to resolve exotic fractional quantum hall states in $GaAs / AlGaAs$ heterostructures requires specialized experimental expertise and a few hundred thousand dollar dilution refrigerator. Exploring new methods of refrigeration, researchers at the Cavendish Lab in the UK recently developed a “quantum dot refrigerator” that is capable of cooling a $6 μ m^{2}$ region of a two-dimensional electron gas (2DEG) to below $190 mK$ [2]. The region of cooled 2DEG is much larger than the size required to fabricate few-electron quantum dots for spin-based quantum control [3].

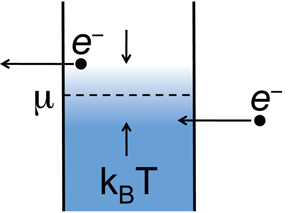
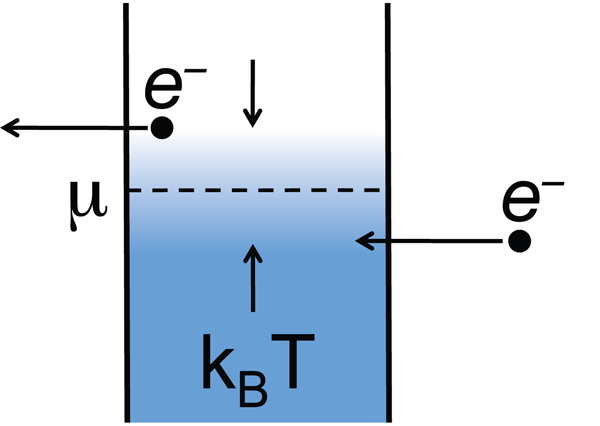
The quantum dot electronic refrigerator was proposed by Edwards and coauthors in the early 1990s [4]. Free electrons at the interface of $GaAs / AlGaAs$ structure—a 2DEG—are isolated in a micron-scale island using electrostatic depletion gates. The island is large enough that the “particle-in-a-box” excited state energies $Δ$ and the electrostatic charging energy $E_{c}$ are smaller than the thermal energy. A simplified energy level diagram is shown in Fig. 1. Electronic states of the island are filled up to the chemical potential $μ$ , following a Fermi-Dirac distribution. To achieve cooling, low-energy electrons are injected into the island and high-energy electrons are removed from the island. Ideally, this process removes $\sim k T$ of energy from the island per electron, resulting in cooling.

A specific electronic operating point is required for efficient cooling. The reason for this stems from the nature of the Fermi-Dirac distribution. First, electrons can only tunnel into unoccupied electronic states on the island. Second, electrons leaving the island can only originate from filled electronic states on the island. Lastly, since the intent is to electronically cool the island, the injected electrons must have a lower energy than the electrons that are removed. These constraints limit electronic transport of electrons in the quantum dot refrigerator to within an energy range $\sim k T$ around the island chemical potential $μ$ . Edwards et al. recognized that in order for this process to work efficiently, an energy-selective source (and drain) of electrons is required [5]. Early experiments used superconducting electrodes as sources and drains, relying on the peaked BCS density of states to provide sufficient energy resolution for efficient electronic cooling [6–8].

The Cavendish team developed an electronic refrigerator that is based entirely on semiconductors [2]. A 2DEG island is in contact with two quantum dots via tunnel barriers. The quantum dots—isolated regions of electron gas—are small enough that the charging and excited state energies are larger than the ambient thermal energy scale. For all practical purposes, the quantum dots can be viewed as artificial atoms, each with its own well-resolved energy-level spectrum specific to the electronic confinement potential. Moreover, the discrete energy-level spectrum of the quantum dots provides a “sharp” density of states for tunneling onto and off the central island.

The refrigerator is created by placing the quantum dots and island in series in the order dot-island-dot. Electron flow is driven by applying a small bias voltage across the device. The resulting current is measured as a function of two gate voltages, each of which couples to a small quantum dot. Physically, the gate voltage shifts the ladder of particle-in-a-box quantum states in the small quantum dots, with a more negative voltage raising the energy of the states in the quantum dot. Following the argument above, electronic transport will only take place through the series device when an energy level in the source quantum dot and drain quantum dot are both within $\sim k T$ of the chemical potential of the central island. Shifting one of the quantum dots out of resonance with the chemical potential of the central island blocks transport, as observed in the experiment.

Based on this simple picture, one might anticipate square regions of nonzero current in the two-dimensional gate voltage parameter space, corresponding to the situation for which energy levels in the source and drain quantum dots are within $k T$ of the central island chemical potential. The experimental data approximate this, but with at least one striking difference: the data are not symmetric about the center of the nonzero current region. To understand this deviation, we can focus on two specific source-drain energy level configurations. The schematic energy diagram shown in Fig. 1 corresponds to the case of electronic cooling. Here the discrete level in the source quantum dot is at a lower energy than the discrete level in the drain quantum dot. Transport of one electron through the series device then removes energy of order $k T$ from the central island resulting in cooling. By making the gate coupled to the source quantum dot more negative and the gate coupled to the drain quantum dot more positive, it is possible to heat the central island. Now an electron enters the island with a higher energy than the electron leaving the island. Transport of a single electron through the device then deposits energy on the central island. Efficient cooling is therefore localized to specific locations in the gate voltage parameter space. Cooling (heating) the central island limits (expands) the range of allowed energies for electron tunneling. The picture then explains why regions of the experimental data where cooling takes place are sharper than the other regions with nonzero current.

The Cavendish team models the cooling/heating generated by the current flow using a master equation approach. Thermal equilibrium is achieved by balancing the electronic cooling/heating process with thermal transport due to coupling of the electrons to lattice vibrations (acoustic phonon coupling). In addition, energy levels in the small quantum dots are lifetime broadened due to a finite tunnel coupling to the source and drain electrodes. This broadening is a major limitation of the cooling process and is accounted for in the model. By fitting the experimental data, the authors demonstrate cooling of the island from an ambient electron temperature of $280 mK$ down to $190 mK$ . Experimental data obtained below $120 mK$ deviate from theoretical predictions.

Based on these results, should low temperature experimentalists consider mothballing their dilution refrigerators? Probably not. Typical quantum dot charging and excited state energies are less than $1 meV$ ( $\sim 12 K$ ), limiting the maximum operating temperature to well below this value. In addition, the cooling power of the Cavendish group device is roughly $90 fW$ , which should be compared with the $100 μ W$ cooling power provided by most dilution refrigerators. However, considering the small size of the sample fabricated by the Cavendish group the results are very impressive.

One unexpected result of this work is the deviation between experiment and theory at the lowest temperatures. A similar experiment by Nahum et al., which utilized superconducting electrodes to create sharp features in the electronic density of states, also reported deviations from theory below $100 mK$ [6]. These results suggest that the cooling process is resulting in a nonequilibrium distribution of electrons in the cooled island. Since the ultimate temperature of the refrigerator is limited by coupling of electrons on the island to the environment, the electronic refrigerator may be an important device for future experiments probing electron-phonon and electron-electron interactions in quantum confined systems.

References

One recent exception is graphene, where quantum Hall physics has been observed at room temperature. See, for example, K. S. Novoselov, et al., Science 315, 1379 (2007)
J. R. Prance, C. G. Smith, J. P. Griffiths, S. J. Chorley, D. Anderson, G. A. C. Jones, I. Farrer, and D. A. Ritchie, Phys. Rev. Lett. 102, 146602 (2009)
R. Hanson et al., Rev. Mod. Phys. 79, 1217 (2009)
H. L. Edwards, Q. Niu, and A. L. de Lozanne, Appl. Phys. Lett. 63, 1815 (1993)
H. L. Edwards, Q. Niu, G. A. Georgakis, and A. L. de Lozanne, Phys. Rev. B 52, 5714 (1995)
M. Nahum, T. M. Eiles, and J. M. Martinis, Appl. Phys. Lett. 65, 3123 (1994)
M. M. Leivo, J. P. Pekola, and D. V. Averin, Appl. Phys. Lett. 68, 1996 (1996)
O-P. Saira et al., Phys. Rev. Lett. 99, 027203 (2007)

About the Author

Jason Petta is an assistant professor in the department of physics at Princeton University. His research is focused on the control of quantum coherence in semiconductor nanostructures (http://pettagroup.princeton.edu).