Turn off the lab furnace and boot up the mainframe
Physics is basically an experimental science, but it is fair to say that not all experiments yield exciting new insights. Even though they provide results of great practical importance, many measurements are exhaustingly time consuming and routine. Imagine if we could reduce the time spent on the more mundane aspects of experimental work with fast and cheap theoretical calculations. This is exactly what is happening in the field of materials science. In a paper appearing in Physical Review B titled “Ab initio up to the melting point: Anharmonicity and vacancies in aluminum,” Blazej Grabowski, Lars Ismer, Tilmann Hickel, and Jörg Neugebauer at the Max-Planck-Institut in Düsseldorf, Germany, show how quantum mechanics is entering their laboratory for steel research [1].
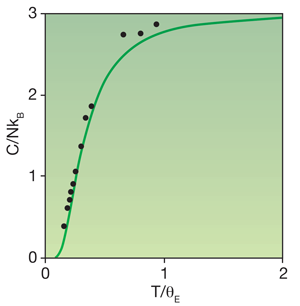
The quantum description of solids began almost exactly 100 years ago. Although Albert Einstein is primarily known for his theory of relativity, and was awarded the Nobel Prize for work on the photoelectric effect, he earned a place in all solid-state physics textbooks for his model, developed in 1906, of the heat capacity of diamond. It had been known since 1819 that the heat capacity of solid chemical elements had an almost universal value—this was the celebrated Dulong-Petit law. Diamond was a striking exception, with a heat capacity at room temperature that was well below the anticipated classical value. Einstein showed that if the carbon atoms were modeled as perfect harmonic oscillators, quantum effects would make the heat capacity vanish at zero kelvin but be in agreement with the Dulong-Petit law at high temperature.
However, at high temperatures all solids show a heat capacity that is larger than predicted by the Einstein model (Fig. 1). The main reason is a partial breakdown of the assumption that atomic vibrations are harmonic. Further, although Einstein allowed for quantum effects in the form of a discrete energy spectrum, his work was almost two decades before the discovery of quantum mechanics. He therefore had to fit the vibration frequencies of the carbon atoms to experiments rather than calculate them from the Schrödinger equation, as one can do today. The paper by Grabowski et al. takes these points to a new depth, the operative words in the title of their paper being “ab initio” and “up to the melting point.”
Ab initio means that no experimental data enter the calculation beyond the building blocks of the solid, i.e., the atoms, which are characterized by a given number of electrons and a nucleus of known charge and mass. Ab initio calculations of energies got their breakthrough in the 1990s. But those calculations were almost always performed at absolute zero temperature. The atoms were either assumed to take the positions of a perfect lattice, or they were sitting rigidly in a deformed “frozen lattice” structure. Parallel to the development of ab initio methods, anharmonic effects were modeled in molecular dynamics calculations, which use classical physics, and solve Newton’s equation of motion. The atoms are represented by particles with given masses and interactions and the interaction is described with a potential in a simple mathematical form, for instance the Lennard-Jones potential.
The challenge has been to combine the ab initio approach with a dynamical lattice at high temperatures. These efforts now start to bear fruit, with the paper by Grabowski et al. being the most ambitious so far. The energies for various atomic configurations, obtained by solving the Schrödinger equation, are combined with a statistical mechanics description to get the free energy of the system as a function of temperature and volume. The paper deals with pure aluminum, which may seem to be a far shot from real materials like highly sophisticated steels, but the task—to achieve such accuracy that theory can replace experiments—is still very demanding.
In order to judge if a general theoretical approach is accurate enough, one must first make a detailed analysis of special systems. Aluminum is a natural choice in this case. There are good experimental heat capacity data available and the deviation from the classical Dulong-Petit law at high temperatures is large enough to present a theoretical challenge. In particular, the theoretical analysis should identify the contributions from anharmonic lattice vibrations, electronic excitations, and the formation of lattice defects (primarily vacancies). When the results of Grabowski et al. are confronted with experiments, including data for the thermal expansion and the vacancy concentration, the agreement is found to be good but still far from perfect. This is expected, both because there is a spread in the experimental results and because one can choose between different theoretical approximations. However, just as important as a close agreement with experiments is the author’s development of a new, and technically elaborate, calculational scheme, which shortens the required computer time very significantly.
In materials science, the free energy is a key physical property since it determines the phase diagram of the system. From the elements in the Periodic Table one can form several thousand binary combinations, which could potentially be of practical use provided we have good knowledge about their phase diagrams. Modern materials often contain ten or more different elements and it is obvious that experimentally determining the phase diagrams for even a very small fraction of all these systems is absolutely impossible. Compare this with the prospect of replacing experiments with theoretical calculations. It requires smart algorithms, so that one can make full use of the existing computer capacity. It also requires a physical insight to ensure that the results are properly interpreted. The work by Grabowski et al. lies at the cutting edge in these respects, and the pace in such theoretical progress will not slow down. In combination with steadily increasing computer capacity, it means that tomorrow’s scientists in traditional areas like the steel industry may marvel at what they can do with quantum mechanics.
References
- B. Grabowski, L. Ismer, T. Hickel, and J. Neugebauer, Phys. Rev. B 79, 134106 (2009)
- A. Einstein Ann. Physik 22, 180 (1906)