Super resolution with superposition

Petr M. Anisimov; Jonathan P. Dowling

Viewpoint

Super resolution with superposition

Petr M. Anisimov and Jonathan P. Dowling

Hearne Institute for Theoretical Physics, Department of Physics and Astronomy, Louisiana State University, Baton Rouge, Louisiana 70803

June 22, 2009• Physics 2, 52

A proposal for obtaining optical resolution better than the classical limit by means of spatially entangled quantum states of light opens a new frontier in the fields of quantum optical imaging, metrology, and sensing.

Figure caption — **Figure 1:** (Top) Dizzy Dean throws curveballs made of ordinary unentangled single baseballs (photons) at a target, and his probability of hitting the bull’s eye improves only as $1 / \sqrt{N}$ , where $N = 4$ is the number of balls thrown. (Bottom) Here Dean throws a single quantum ball composed of $N = 2$ photons in a spatially entangled N00N state, and with a little postprocessing carried out by a computer at the target, the chances of hitting the bull’s eye now scales like $1 / N$ .

Optical imaging and lithography, the processes in which spatial patterns are resolved or transferred onto a detector or substrate via photons, cannot produce spatial features that are much smaller than the wavelength of light. This limitation has its roots in classical diffraction [1], which had been considered as a fundamental limit to all such imaging systems. Most notably, computer chip manufacturers have been moving to ever-shorter wavelengths and thus need to solve the challenges associated with use of extreme ultraviolet light. These include the lack of cheaply available optical elements that operate at such short wavelengths, and the damaging effects such high-energy photons have on the imaging elements and the photoresist. Nearly ten years ago, a quantum optical approach to imaging—quantum imaging, which uses path-entangled states—was suggested as a solution for this requirement of ever-shorter wavelengths and a way to beat the classical limit [2]. This turned out to be easier said than done. While quantum lithography is viewed as one of the “killer apps” for the nascent field of quantum imaging, the bugaboo in its implementation has been the continued lack of the right kind of multiphoton photoresists that would operate at the low flux levels required for a real proof-of-principle experiment.

In a paper appearing in Physical Review Letters, Mankei Tsang at the Research Laboratory of Electronics of MIT has proposed an end-run around this resist problem by exploiting a radically new approach to the optical detection of nonclassical states of light [3]. Tsang has found a way to extract the fabled sub-Rayleigh quantum resolution for imaging using simple intensity measurements and a bit of numerical postprocessing, which mitigates the need for elaborate detection schemes. Tsang’s new measurement scheme does not by itself solve challenges that specifically face quantum lithography, particularly the photoresist problem, since it involves intensity measurements followed by image postprocessing in order to produce quantum interference patterns. Nevertheless, Tsang’s proposed scheme allows efficient detection of spatially entangled states of light, which is, at the very least, a tool to test the limits to optical resolution in quantum imaging systems. What’s more, by encoding images or phase information in a special manner, quantum imaging and quantum sensing beyond standard limits on resolution and sensitivity becomes a reality with currently available technology.

The broader field of quantum imaging—of which quantum lithography is only a small subset—is based on the idea that an ensemble of $N$ photons, each with classical wavelength $λ$ , can be regarded as a single quantum object with $N$ times the energy of a single photon, and thus an effective wavelength of $λ / N$ , called the photonic de Broglie wavelength [4]. N00N states are a well-known example. Their name stems from the fact that they are combinations of $N$ photons in one path (say, of a two-arm interferometer) and $0$ photons in another, and vice versa ( $N 0 + 0 N$ ). These states are akin to what have come to be called “Schrödinger cat states” in quantum information theory, namely superpositions of macroscopic entities that upon measurement are found in one state or another [5].

Detection of N00N states with single-photon absorbers cannot reveal the collective catlike behavior because by detecting one photon (a whisker) it provides “which-path” information for the rest of the cat and collapses its state—dead or alive. Boto et al. showed that only a $N$ -photon-absorber-based detection of N00N states could elicit patterns exhibiting this $N$ -fold de Broglie super resolution [2]. However, the process of $N$ -photon absorption (for lithography) is equivalent to $N$ -photon detection (for imaging) and so N00N states can be used in a number of imaging systems that strive to beat poor old Lord Rayleigh.

The development of a photoresist with efficient multiphoton absorption has been a stumbling block on the way to an experimental realization of large-scale quantum lithography and still remains a hot topic of ongoing research. However—in the broader context of quantum imaging, metrology, and sensing— $N$ -photon coincidence detection could be implemented as a workaround of the multiphoton photoresist problem. Alas, coincidence detection is very inefficient, especially in the limit of large $N$ , and serves only for proof-of-principle experiments with very few photons. The inefficiency comes from the fact that all $N$ photons are expected to arrive at the same point of space, or at all of the detectors, at the same time—which intuitively is highly unlikely, but which also seems to be a natural requirement of any imaging system that relies on $N$ -photon coincidence. Contrariwise, the requirement for all $N$ photons to be in the same spatial mode implies that they are all momentum-correlated—as well as spatially anticorrelated (maximally spread out in space). These two features are complementary to the requirement that they all arrive at the same detector (or atom) at the same time.

Tsang’s marvelous proposal gets around these seemingly incompatible conditions by providing a detection scheme that is itself nonlocal. That is, the scheme is reminiscent of the so-called “quantum eraser” in that the scheme detects photons that are scattered all over the imaging plane, but it does not record individual detection locations [6]. Instead, the method relies on computation of the collective quantity—the optical “centroid”—which is the center of gravity of the photon clicks. In this way “which-path” information is never revealed upon detection, and so the coherence of the entangled N00N state is not destroyed. This in turn means the sub-Rayleigh super-resolution can be extracted—using ordinary, run-of-the-mill photodetectors. Tsang performs this trick by suggesting the deployment of an array of photon-number-resolving detectors—or the more readily available single-photon detectors—subject to the constraint that there is a sufficient number of them within the “real” optical wavelength $λ$ , so that the higher resolution pattern can be recorded, while keeping the probability of two photons arriving at the same detector negligible.

The optical centroid measurements then do the rest of the job by taking into account all the detection events at once, thus improving on conventional $N$ -photon coincidence detection. However, in Tsang’s proposal the individual detection events do not produce quantum interference patterns, but rather require image postprocessing to reveal the patterns, which excludes the use of this technique for lithography, unless you have very smart atoms in the resist. It is important to note that multiphoton absorbers, and thus conventional coincidence detectors, produce quantum interference patterns without image postprocessing because they intrinsically perform conditional optical centroid measurements.

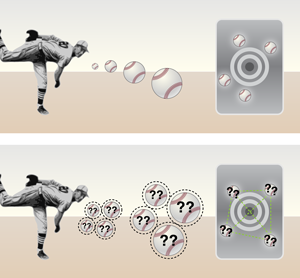
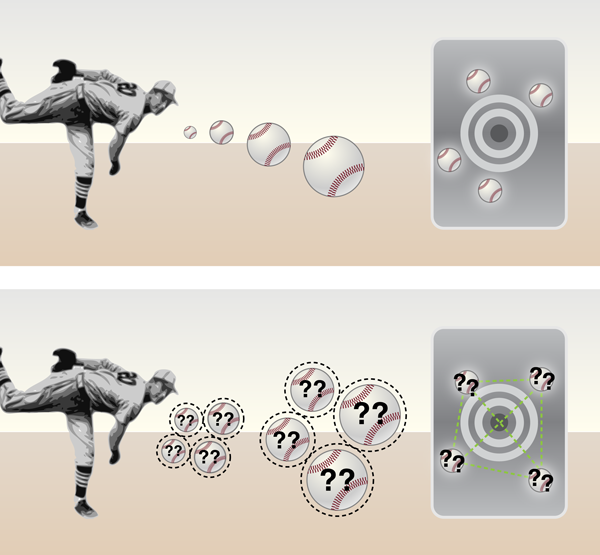
Optical centroid measurements with $N$ independent photons is sort of like baseball batting legend Babe Ruth watching iconic pitcher Dizzy Dean throw his infamous curveball $N$ times over the home plate (Fig. 1). Classically, the Babe’s prediction about the location of the spot that Dizzy was aiming at improves only as $1 / \sqrt{N}$ , which slowly increases his chance to strike a homerun on the next pitch. However, optical centroid measurements with $N$ entangled photons, since they can be made spatially anticorrelated, is akin to a game of quantum baseball with Dizzy throwing $N$ curveballs in such a way that if one strikes to the left of the home plate, there will be a correlated one that inevitably strikes to the right of the plate, so that the maximum uncertainty in position is obtained. Nevertheless, the aim of the pitcher is localized by the centroid measurement with a precision that is $\sqrt{N}$ times better than the independent “classical” photon case, since deviation of any one photon is compensated by the rest. In a similar fashion, $N$ momentum correlated (spatially anticorrelated) photons serve as a very precise displacement detector.

The requirements for the emerging fields of quantum imaging, metrology, and sensing quite often coincide [7]. Progress in these areas over the last twenty years has been made by improving quantum optical sources (spontaneous parametric down-converters, parametric amplifiers and oscillators) and optical processors (phase shifters, beam splitters, and mirrors), but the detection schemes always seemed to be the stumbling block. Mythical $N$ -photon absorbing resists and nasty $N$ -photon coincidence detection schemes always seemed to rule the field. Not anymore! In one fell swoop, Tsang sweeps away this requirement for $N$ -photon detection. This exciting centroid work of Tsang opens the ballgame up in an a entirely new and practical way, and moves quantum interferometry one step further from being a funhouse curio, and one step closer to becoming a usable technology.

References

M. Born and E. Wolf, Principles of Optics (Cambridge University Press, Cambridge, UK, 1999)[Amazon][WorldCat]
A. N. Boto, P. Kok, D. S. Abrams, S. L. Braunstein, C. P. Williams, and J. P. Dowling, Phys. Rev. Lett. 85, 2733 (2000)
M. Tsang, Phys. Rev. Lett. 102, 253601 (2009)
J. Jacobson, G. Björk, I. Chuang, and Y. Yamamoto, Phys. Rev. Lett. 74, 4835 (1995)
Erwin Schrödinger’s original 1935 gedanken experiment was intended to ridicule the Copenhagen interpretation of quantum mechanics by imagining an unfortunate cat sealed in a box with radioactive isotope and a Geiger counter that would trigger release of poison upon detection of a random radioactive decay event. Before a measurement was performed (opening the box) the macroscopic classical object (the cat) would presumably be in an entangled state of being “dead” and “alive.” Nowadays, “cat states” in quantum information theory refer to macroscopic entangled states such as the N00N states in which $N$ photons are grouped together and can take one of two possible routes in a manner such that no “which-path” (or “which-cat”) information is available. One does not know if all $N$ photons are in one path (live cat) or if all $N$ photons are in the other path (dead cat)
M. O. Scully and K. Drühl, Phys. Rev. A 25, 2208 (1982)
J. P. Dowling, Contemporary Physics 49, 125 (2008)

About the Authors

Petr M. Anisimov obtained his M.S. in physics, Summa Cum Laude, from Nizhniy Novgorod State University, Russia, in 2001 and his Ph.D. in quantum optics from Texas A&M University, USA, in 2008. He is currently a Postdoctoral Researcher at the Louisiana State University in Baton Rouge, Louisiana. His main interests are path-entangled number states and multiphoton absorption and detection.

Jonathan P. Dowling is the Hearne Professor of Theoretical Physics and Director of the Hearne Institute for Theoretical Physics at Louisiana State University, Baton Rouge, Louisiana. He received his Ph.D. in mathematical physics in 1998 from the University of Colorado at Boulder. He has held positions at the International Center for Theoretical Physics in Trieste, Italy, the Max Planck Institute for Quantum Optics in Garching, Germany, the Army Aviation and Missile Command, Huntsville, Alabama, and the Jet Propulsion Laboratory, Pasadena, California. Dowling has over 125 published articles, and holds eight US patents in the fields of nonlinear and quantum optics. He is a Fellow of the American Physical Society and a Fellow of Optical Society of America, and has served on the editorial boards of the Physical Review, the Journal of the European Optical Society, and Concepts of Physics. He has been awarded the Willis E. Lamb Medal for Laser Science and Quantum Optics, the US Army Research and Development Achievement Award, the NASA Space Act Award, and was runner up for the Discover Magazine Technology of the Year Award in 2001.