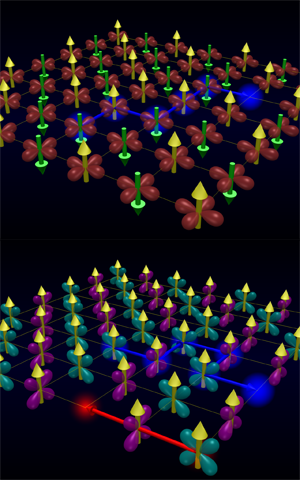
Challenging a hole to move through an ordered insulator

Mona Berciu

Viewpoint

Challenging a hole to move through an ordered insulator

Department of Physics and Astronomy, University of British Columbia, Vancouver, British Columbia, Canada V6T 1Z1

June 29, 2009• Physics 2, 55

A theoretical framework to explain how a hole moves through an antiferromagnetically and orbitally ordered lattice could also provide insight into the interplay between these two ordered phases.

Figure caption — **Figure 1:** (Top) The string of defects (emphasized by blue halos) that are generated by hole motion in an antiferromagnetic background can be “healed” by quantum fluctuations. (Bottom) A similar string of defects (blue halos) is generated by zigzag hole motion in an alternating-orbital-order background (the green and purple lobes represent orbitals with $x z$ and $y z$ symmetry, respectively). These cannot be healed by quantum fluctuations and instead the hole has to do it by retracing its steps. Overall hole motion is enabled by three-site processes (red halos), consisting of directional tunneling through a doubly occupied site without generating a defect.

This is a difficult question, and enormous theoretical effort has been (and still is) devoted to answering it. On one hand, we know from experimental data that these holes are mobile, since the doped systems quickly become metallic. On the other hand, it is hard to see how the hole can move at all given the type of order of the parent compounds: in cuprates, the spins form an antiferromagnetic arrangement at low temperatures (as in the top part of Fig. 1), while in manganites, the spatial distribution of the $3 d$ orbitals on the $Mn$ sites forms a pattern of alternating orbital order (similar, though not identical, to the bottom of Fig. 1). Since in both cases, the proper alternation of the spins or orbitals is disrupted as the hole moves through the lattice, one might expect that the hole cannot go too far from its original location.

Writing in Physical Review B, Krzysztof Wohlfeld, Andrzej Oleś, and Peter Horsch of the Max Planck Institute in Stuttgart, Germany, take the next step and for the first time address the issue of a hole moving in an insulator that has, simultaneously, both antiferromagnetic and alternating orbital order [1]. Beyond the direct implications of their results for real materials that possess both types of order, such as ${LaVO}_{3}$ , their study begins to address the effects of the interplay between two different types of “alternating” orders—a long-standing question in the study of a number of other materials, including some of the manganites.

Before discussing their findings, it is instructive to review what is known about the motion of a charge carrier in materials with simpler types of order. The only case with a known exact solution at zero temperature is long-range ferromagnetic order with no orbital degeneracy (that is, there is only one orbital that can be occupied) [2,3]. This occurs, for example, in the ferromagnetic insulator $EuO$ . A charge carrier with a spin parallel to this ferromagnetic background propagates without any hindrance since no spin-flipping processes are possible. If, on the other hand, the charge carrier’s spin is antiparallel to the background, it oscillates between propagating freely and flipping its spin to be parallel to the background, at the price of a simultaneous flip of a spin that make up the ferromagnetic background. (The reason this process can occur is rooted in the fact that the magnetic exchange between the charge carrier’s spin and the spins in the background has full rotational—Heisenberg—symmetry.) This results in the excitation of a magnon: a collective excitation of the ferromagnetic background. In favorable circumstances, the magnon becomes bound to the charge carrier and together they form a so-called spin-polaron that propagates coherently. The spin-polaron is a true quasiparticle with an infinite lifetime and a mass somewhat, though minimally, heavier than that of a free electron or hole, because of the bound magnon.

The situation for cuprates is more complex, as the spins on the valence electrons on the copper sites are now ordered antiferromagnetically. Upon hole doping (removal of one electron), it seems that the hole can no longer move freely, in essence, through the system, as in the simpler case of the ferromagnet. This is because, as sketched in the top panel of Fig. 1, as the hole hops around, it reshuffles the spins it visits and creates a “string” of defects that costs significant magnetic (or “exchange”) energy.

An exact solution for how the hole succeeds in being mobile in antiferromagnets like the cuprates is not known, not least because we are missing an exact description of the antiferromagnetic undoped state itself. Two simplifications make this problem easier to solve. One is to forbid having two electrons at the same site because the Coulomb repulsion is so large. In this case, it is possible to describe the collective excitations of the antiferromagnetic background with the linear spin-wave approximation, and the problem reduces to a simpler polaronlike problem [4]. This permits the calculation of the hole’s propagator, which is the amplitude of the probability that the hole evolves from a specified initial state to a specified final state. From the propagator we can determine whether the hole is mobile or not, and its imaginary part—the spectral weight—can be measured by both angle-resolved photoemission and scanning tunneling microscopy.

Even after all these simplifications, the propagator still cannot be calculated exactly. A second simplification is therefore the application of the self-consistent Born approximation, which leads to an accurate solution that compares well with numerical simulations [5]. This is meaningful because this approximation only includes processes where the hole reabsorbs the magnons in the inverse order it emitted them. In other words, the hole indeed retraces its steps and “heals” the string of defects it created. This is supplemented by the fact that two neighboring incorrectly oriented spins can flip each other back to the correct antiferromagnetic order, through their Heisenberg exchange. Thus, we can picture the mobile quasiparticle as consisting of the hole surrounded by a cloud of magnons (flipped spins), which it continuously emits and reabsorbs as it tries to move away and is forced to come back. Every now and then “self-healing” removes some of the defects from this string of defects tying the hole to its initial position and allows it to progress to a new starting point, explaining why it is mobile even though rather slow and heavy.

The motion of a hole in a background of alternating orbital order but with ferromagnetic spin order is somewhat different. Consider a material such as undoped ${Sr}_{2} {VO}_{4}$ with one electron per site occupying either of the two $3 d$ orbitals with $x z$ and $y z$ symmetry (the other $3 d$ orbitals have different energies and their occupation numbers are assumed to be fixed). By symmetry, the occupied orbital determines the allowed hopping: electrons in the $d_{x z}$ and $d_{y z}$ orbitals can only hop along the $x$ and $y$ axes, respectively. This suggests that a hole doped in this type of ordered background moves in zigzags, leaving a string of orbital “defects” behind as sketched in the bottom panel of Fig. 1. Unlike in cuprates, however, there is no “self-healing” possible for these defects because of the Ising-like symmetry of their interactions. So, again one expects the hole to be trapped. This is not the case, as demonstrated recently in Ref. [6], due to “three-site terms,” which appear when the approximation of no double occupancy is enforced, and which allow the hole to tunnel through a doubly occupied configuration without creating a defect (Fig. 1, bottom panel). Such processes have well-defined directionality and result in an even heavier quasiparticle with one-dimensional motion. One can picture it again as the hole creating and undoing strings of orbital defects, and changing its starting point every now and then through directional three-site tunneling.

The new question (see Fig. 2) is what happens if the insulator has both antiferromagnetic and alternating orbital order, as is the case in ${LaVO}_{3}$ ? Wohlfeld et al. use the same simplifications as for cuprates and manganates to reduce the problem to being polaronlike, but now with simultaneous scattering of the hole from both spin waves and orbital waves. They then calculate the spectral weight using the self-consistent Born approximation. This reveals again the appearance of a low-energy mobile quasiparticle, with properties superficially similar to those of a quasiparticle in a background that only has alternating orbital order. As the hole moves along the zigzags allowed by the orbital order, it creates strings of both orbital and magnetic defects. Unlike holes moving in antiferromagnetic-only backgrounds, the defects formed in this more complex case cannot “self-heal” through quantum fluctuations because of the Ising-like nature of the orbitals. So the hole is forced to fully retrace its steps and repair the defects it created. Overall motion is only enabled, as for the case of hole motion in the alternating-orbital-only background, by three-site processes. This results in a heavy quasiparticle with a quasi-one-dimensional dispersion.

These considerations explain the superficial resemblance between this solution and the orbital-only polarons. But Wohlfeld et al. show that the spins also play a key part. The spin dynamics is effectively confined to being Ising-like because of the simultaneous coupling to the alternating orbital order; however, they contribute significantly to the energetics of the system since the strings generated by the hole have joint spin-orbital character.

This work predicts that holes find a way to propagate coherently even through such challenging backgrounds as a lattice with both antiferromagnetic and alternating orbital order. Once this conclusion is confirmed by photoemission experiments, it will open the way to understanding the low-doping part of the vanadate phase diagrams, as well as other materials with similarly complex ordered states.

References

K. Wohlfeld, A. M. Oleś, and P. Horsch, Phys. Rev. B 79, 224433 (2009)
B. S. Shastry and D. C. Mattis, Phys. Rev. B 24, 5340 (1981)
M. Berciu and G. A. Sawatzky, Phys. Rev. B 79, 195116 (2009)
See, for instance, G. Martinez and P. Horsch, Phys. Rev. B 44, 317 (1991)
See, for instance, A. S. Mishchenko, N. V. Prokof’ev, and B. V. Svistunov, Phys. Rev. B 64, 033101 (2001)
M. Daghofer, K. Wohlfeld, A. M. Oleś, E. Arrigoni, and P. Horsch, Phys. Rev. Lett. 100, 066403 (2008)

About the Author

Mona Berciu received her B.Sc. from the University of Bucharest in Romania in 1994 and her Ph.D. from the University of Toronto in 1999. After postdoctoral work at Princeton University, in 2002 she moved to the University of British Columbia where she is currently an Associate Professor.