Molecules on a string

Adela  Marian; Bretislav  Friedrich

Viewpoint

Molecules on a string

Fritz-Haber-Institut der Max-Planck-Gesellschaft, Berlin, Germany

September 14, 2009• Physics 2, 76

An electric field can be used to pull on molecular hydrogen’s highly excited outer electron to slow down and trap the molecule.

Figure caption — **Figure 1:** Simulations of phase-space distributions showing the velocity vs position of the molecular cloud of $H_{2}$ in the $n = 30$ Rydberg state at different junctures of the deceleration and trapping process. When created by photoexcitation at position and time zero, the Rydberg molecules have a mean longitudinal velocity of $500 m / s$ . In about $10 μ s$ the molecules are decelerated over a longitudinal distance of only $3 mm$ to zero mean velocity. At this position the molecules are then held in an electrostatic trap for about $50 μ s$ . At any juncture, the molecules can be field-ionized and detected. Apart from reflecting the inhomogeneity of the electric field applied, the distributions illustrate that the conservative Stark interaction does not increase phase-space density (the density of points in each of the subsequent distributions).

Over recent decades, atomic and molecular physics has blossomed, with much of the work springing from new techniques to translationally manipulate—especially to slow and trap—gaseous atoms and molecules. The ensuing study of slow (cold) atoms and molecules has led researchers into uncharted territories—not just of atomic and molecular physics, but of physics and even chemistry at large. Achieving manipulation on the atomic or molecular level requires some hook by which a magnetic or electric field can seize the atoms or molecules. The role of such a hook is played by the magnetic or electric dipole moment, whose magnitude determines how strong the pull of a given field will be.

In order for a molecular magnetic dipole moment to be sizable (on the order of 1 Bohr magneton), the molecule must be in an open-shell state with nonzero electronic angular momentum. The ground states of radicals (that is, species with unpaired electrons, which makes them more than willing to undergo chemical reactions) all fall into this category and thus exhibit paramagnetism. Most molecular electronically excited states are paramagnetic, for the same reason that the ground states are not, since excitation typically entails raising angular momentum. To give a sense of scale, the interaction energy of a molecular magnet carrying a dipole moment of 1 Bohr magneton with a magnetic field of 1 tesla is $0.67 K$ . This so-called Zeeman energy thus represents only about $0.2 %$ of thermal energy ( $300 K$ ). Molecular electric dipole moments, which result from differences in electronegativity of the constituent atoms (that is, their ability to attract electrons), are typically on the order of a debye. In order for such a dipole moment to have an interaction energy (Stark energy) equal to the Zeeman energy of $0.67 K$ , the electric field strength must be $28 kV / cm$ . Since laboratory electrostatic fields are limited to about four times as much, the Stark energy of a polar molecule falls far short of the thermal energy, to only about a $1 %$ level. As Stephen Hogan, Christian Seiler, and Frédéric Merkt from the ETH Zurich show in a paper in Physical Review Letters [1], something can be done about this: the Stark energy of a molecule can be boosted by exciting it to a highly polar Rydberg state in which an electron is put in high orbit. After the manner of a puppeteer, an electric field can then pull on the molecule’s Rydberg electron, like pulling on a string, with the result of manipulating the molecule to and holding it at standstill. The idea of Rydberg-Stark manipulation was originally proposed by Wing [2] and by Breeden and Metcalf [3] in the early 1980s, and its implementation has been a recurring daydream in the atomic, molecular, and optical physics community ever since.

A Rydberg state comes about when a molecule’s electron is promoted to an orbital with a high principal quantum number $n$ (for a review, see Ref. [4]). The spatial separation of the electron in such an orbital with respect to the molecule’s ionic core is large, and thus the concomitant dipole moment is also large, even if the ground-state molecule is nonpolar. For instance, the (nonpolar) $H_{2}$ molecule in its $n = 30$ Rydberg state is endowed with a dipole moment of $3000$ debye, more than $2000$ -fold that of ammonia in its ground state. As a result, a modest electrostatic field of about $4 kV / cm$ has a grip on $H_{2} (n = 30)$ that amounts to the full $300 K$ thermal energy.

The large dipole moments make Rydberg states susceptible to field ionization, which puts a limit on the maximum field strength that can be applied to manipulate them. On the other hand, field ionization can be used to sensitively detect the Rydberg molecules. The large dipole moments also shorten the radiative lifetimes of Rydberg molecules. Fortunately, not all Rydberg states are created equal, and one can pick a state whose decay is more forbidden than that of the others. In particular, Rydberg states with nonpenetrating orbitals are long-lived, often with a lifetime in excess of tens of microseconds, since their overlap with the core wave functions, which drives relaxation, is limited.

Over the last decade, ammonia and other polar molecules were successfully slowed down by Stark deceleration and subsequently loaded into electrostatic/dynamic traps or storage rings [5]. Stark deceleration relies on a loss of kinetic energy, which, by virtue of energy conservation, is brought about by a coerced gain of Stark potential energy in an inhomogeneous electric field. For instance, ammonia molecules with a forward translational energy of about $100 K$ were brought to a standstill by being forced to successively climb about $100$ Stark energy hills, generated by switching electric fields between zero and about $100 kV / cm$ . With Rydberg molecules, thanks to their giant electric dipole moments, the same feat can be achieved by just a single deceleration stage (no switching involved) generated by a modest electric field of just a few $kV / cm$ . In principle, this approach is applicable to any Rydberg molecule (or atom) in the gas phase, provided their lifetime is long enough. Rydberg-Stark manipulation was first demonstrated in 2001 by Townsend et al. [6] at the University of Oxford, who observed a sizable deflection of $Kr$ ( $n = 16$ – $19$ ) atoms in a dipole electrostatic field.

The story Hogan et al. tell contains intriguing detail about both the dynamics of Stark manipulation and the spectroscopy of the Rydberg states involved. Among the challenges of the experiment was the excitation of the molecular hydrogen’s Rydberg electron to a nonpenetrating orbital, to ensure a long lifetime of the Rydberg state, needed for deceleration, trapping, and detection. In other words, the authors had first to map out the Rydberg states of $H_{2}$ and their Stark effect so that suitable Rydberg manifolds—such that have little overlap with others—could be identified. The manifolds they settled on, with $n = 22$ – $30$ , were then accessed by a combination of three circularly polarized laser beams acting on a pulsed supersonic beam of $H_{2}$ and spanning the $VUV (105 nm)$ , visible ( $550 nm$ ), and $IR (840 nm)$ domains. The $H_{2}$ beam was inversely seeded in $Kr$ so that the most probable velocity of $H_{2}$ was $500 m / s$ (corresponding to a forward translational energy of about $30 K$ ). The use of circular polarization ensured the formation of properly oriented $f$ -type orbitals, which are nonpenetrating. The Rydberg spectra were recorded by detecting the ion signal generated from the molecules by pulsed field ionization as a function of the tunable frequency of the IR laser.

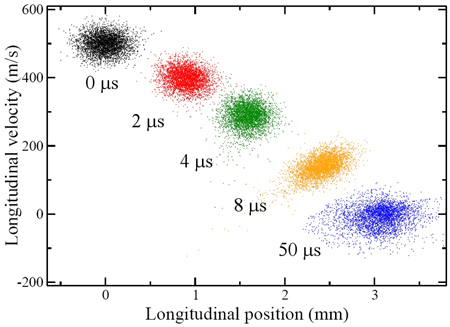
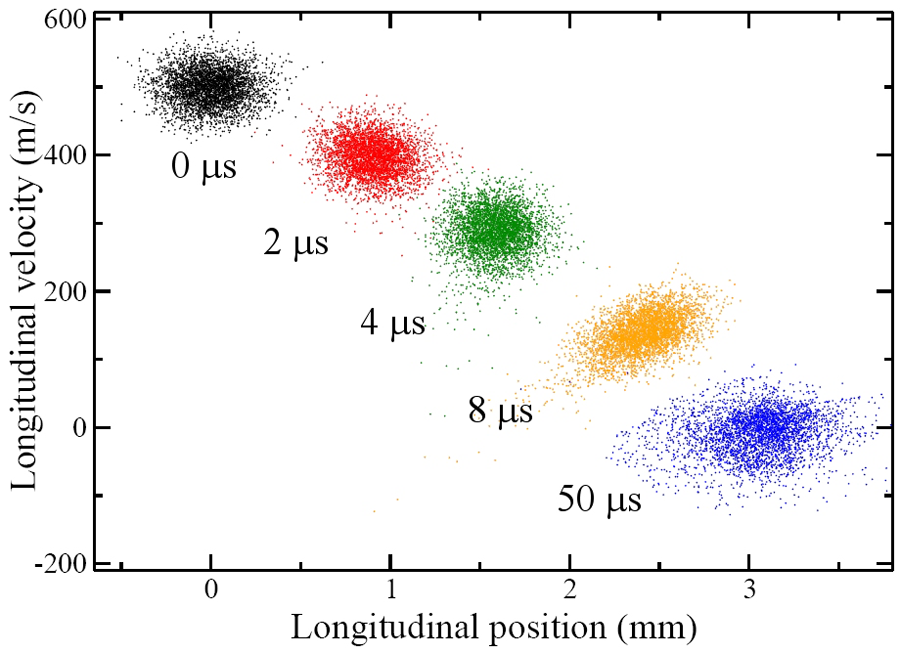
On their flight towards the detection region, the Rydberg molecules were subjected to a fast decaying electric-field pulse, which furnished the necessary inhomogeneous field without causing premature field ionization: ramping down the field maintained the force induced by the field gradient acting on the forward-moving molecules but prevented the molecules from exposure to an ionizing field strength. This was a key enabling trick. The set of six electrodes used for the preparation and deceleration of the Rydberg molecules was then re-energized to a configuration that gave rise to a Stark trapping potential (a minimum of electric field strength in free space, yielding trapping action for low-field seekers). Since both the deceleration and trapping procedures depend on the magnitude of the electric dipole moment, $H_{2}$ molecules in a range of $n$ states could be loaded and trapped. This was because the dipole moment is proportional to the product $n k$ , where $k$ , on the order of $n$ , depends on the “eccentricity” of the Rydberg orbital. The “acceptance” of the Stark decelerator and trap differs for different Rydberg states, as larger fields afford deceleration and trapping of Rydberg states with a lower dipole moment (lower value of $n k$ ). The authors estimate that about $60 %$ of the decelerated molecules could be loaded into the trap, at a density of $10^{7}$ – $10^{8}$ molecules per ${cm}^{3}$ and at a temperature of about $150 mK$ (see Fig. 1). The trap lifetime was measured to be about $50 μ s$ , chiefly limited by collisions with background gas, but clearly long enough to afford extracting a plethora of clear and revealing data about both the states involved and their trap dynamics.

In their earlier work, the ETH group joined forces with the group at Oxford to Stark- decelerate molecular hydrogen, tapping a different Rydberg manifold [7]. Subsequently, the ETH group demonstrated Stark deceleration and trapping of Rydberg hydrogen atoms [8]. Achieving now the same feat with hydrogen molecules is particularly significant, given the versatility of the Rydberg-Stark technique and the otherwise limited means available to slow and trap nonpolar and nonmagnetic molecules.

References

S. D. Hogan, C. Seiler, and F. Merkt, Phys. Rev. Lett. 103, 123001 (2009)
W. H. Wing, Phys. Rev. Lett. 45, 631 (1980)
T. Breeden and H. Metcalf, Phys. Rev. Lett. 47, 1726 (1981)
F. Merkt, Annu. Rev. Phys. Chem. 48, 675 (1997)
S. Y. T. van de Meerakker, H. L. Bethlem, and G. Meijer, in Cold Molecules: Theory, Experiment, Applications, edited by R. V. Krems, W. C. Stwalley, and B. Friedrich (CRC/Taylor and Francis, Boca Raton, 2009), pp. 509-554[Amazon][WorldCat]
D. Townsend, A. L. Goodgame, S. R. Procter, S. R. Mackenzie, and T. P. Softley, J. Phys. B 34, 439 (2001)
Y. Yamakita, S. R. Procter, A. L. Goodgame, T. P. Softley, and F. Merkt, J. Chem. Phys. 121, 1419 (2004)
S. D. Hogan and F. Merkt, Phys. Rev. Lett. 100, 043001 (2008)

About the Authors

Adela Marian received her Ph.D. in 2005 from the University of Colorado at Boulder, where she worked on cold-atom spectroscopy using a phase-stabilized femtosecond laser. She then moved to the Fritz Haber Institute of the Max Planck Society in Berlin, where she is leading an experiment aiming to sympathetically cool molecules using ultracold atoms. She was a recipient of an Alexander von Humboldt Fellowhip in 2006, as well as of a Marie Curie Fellowship in 2007.

Bretislav Friedrich is Research Group Leader at the Fritz-Haber-Institut der Max-Planck-Gesellschaft, Berlin, Honorary Professor at the Technische Universität Berlin, and Co-Director of the History and Foundations of Quantum Physics Program in Berlin. Among his distinctions is the Outstanding Referee Award of the American Physical Society. He graduated from Charles University, Prague, in 1976, and earned his Ph.D. in chemical physics from the Czech Academy of Sciences in 1981. His experimental and theoretical research at Göttingen (1986–1987), Harvard (1987–2003), and Berlin (since 2003) has dealt with interactions of molecules with fields, cooling and trapping of molecules, collision dynamics, and spectroscopy.