Spins in cold atoms—what a drag!

Marco Polini; Giovanni Vignale

Viewpoint

Spins in cold atoms—what a drag!

Marco Polini

NEST-CNR-INFM and Scuola Normale Superiore, I-56126 Pisa, Italy

Giovanni Vignale

Department of Physics and Astronomy, University of Missouri, Columbia, Missouri 65211, USA

October 19, 2009• Physics 2, 87

Interactions among noncondensed bosonic atoms in a trap can cause one species of atoms accelerated by a magnetic field to drag along another species of atoms that would normally not interact with the field.

Figure caption — **Figure 1:** Illustration of the concept of spin drag in a toroidal trap. Atoms with hyperfine spin projection $m_{F} = 1$ (red circle with arrow) are accelerated by the motive force due to the time-dependent quadrupole magnetic field (blue arrows) of the trap. Due to interactions, the atoms with $m_{F} = 0$ are dragged along.

Electron-electron interactions between closely spaced nanoelectronic circuits constitute an alternative coupling mechanism to the inductive and capacitive couplings of conventional electronics. It was realized early on [1,2] that “Coulomb mutual scattering” between spatially separated electronic systems provides a mechanism for momentum relaxation, which then leads to equalization of drift velocities. This intrinsic friction due to electron-electron interactions is presently referred to as “Coulomb drag” [3–5] and has first been studied experimentally by Gramila et al. [6] and by Sivan, Solomon, and Shtrikman [7] in semiconductor double quantum wells. Now, in a paper in Physical Review Letters, Rembert Duine and Henk Stoof from Utrecht University in the Netherlands add a fresh approach to a different kind of drag physics—the pulling along of spin-aligned ultracold atoms in an optical trap [8].

In order to illustrate the phenomenon of Coulomb drag, consider two neighboring quantum wells, each hosting a two-dimensional electron gas, and drive a constant current on the two-dimensional ( $2 D$ ) electron gas in one of the wells (the “active,” or “drive,” layer). If no current is allowed to flow in the other well (the “passive” layer), an electric field develops whose associated force cancels the frictional drag force exerted by the electrons in the active layer on the electrons in the passive one. The transresistance, defined as the ratio of the induced voltage in the passive layer to the applied current in the drive layer, directly measures the rate $ρ_{D}$ at which momentum is transferred from the current-carrying $2 D$ electron gas to its neighbor. Coulomb drag is ultimately caused by fluctuations in the density of electrons in each layer since two-dimensional layers with uniformly distributed charge will not exert any frictional forces upon each other [3].

This Coulomb drag concept can be extended to other quantum (and classical) fluids with two (or more) distinguishable species that are able to exchange momentum due to mutual collisions. Spin Coulomb drag [9,10], for example, refers to the friction between two populations of electrons that are not spatially separated as in the bilayer Coulomb drag described above, but that have different spin orientations. Spin Coulomb drag has been recently observed by Weber et al. [11].

Spin drag has also been studied in the context of two-component trapped cold Fermi gases [12–15]. Ultracold atomic gases are highly tunable and ideally clean systems in which spin drag might be observed in a truly intrinsic regime. Of course, it must be borne in mind that cold gases are profoundly different from electronic systems due to at least four reasons: (i) atoms are neutral objects and thus do not respond directly to conventional electromagnetic forces; (ii) in the case of atoms, “spin” refers to a combination of electronic and nuclear spin; (iii) spin drag is due to short-range interatomic interactions as opposed to long-range Coulomb interactions; (iv) spin dynamics in these systems occur in an ideally ballistic regime because of the absence of the ordinary complications of solid-state environments such as impurities, phonons, and crystalline defects.

In all the above-mentioned cases of spin drag, the actors that collide in a scattering event are fermions, which obey Fermi-Dirac statistics and the Pauli exclusion principle. The rate $ρ_{D}$ at which momentum is transferred is typically proportional to $T^{2}$ , thus rapidly vanishing as temperature is decreased. The reason for this behavior is essentially Pauli blocking: most of the states in which a fermion with given pseudospin $σ$ might end up after a collision with another fermion of opposite $σ$ are already occupied, and therefore unavailable. Here, the pseudospin $σ$ could be a layer degree of freedom, a real or a hyperfine spin. The rate $ρ_{D}$ thus has to vanish as $T$ $\to$ $0$ . The surprising ineffectiveness of fermion-fermion scattering is also the physical basis on which Landau’s theory of normal Fermi liquids is built [16]. Coulomb and spin Coulomb drag in electronic devices, or spin drag in trapped cold Fermi gases, are thus “small” effects in this sense.

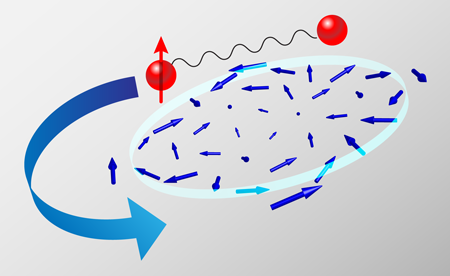
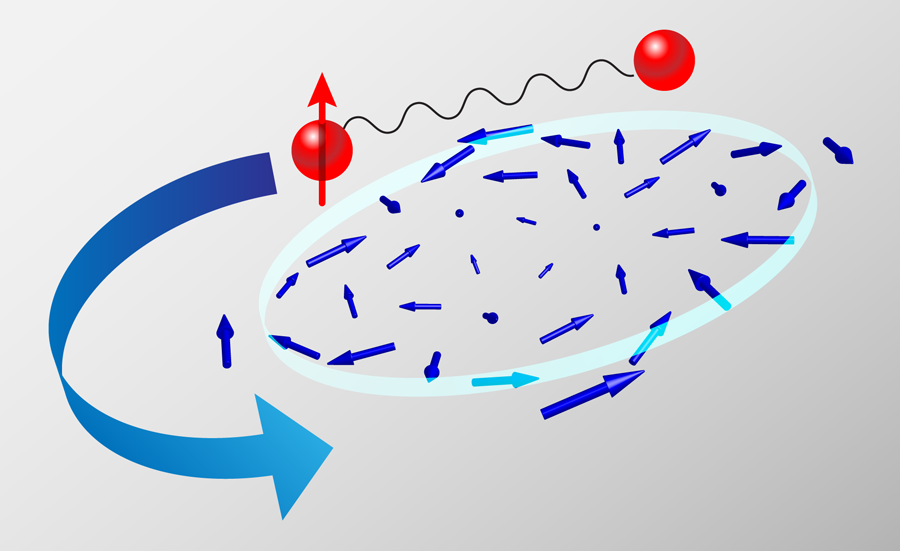
Duine and Stoof now propose an ingenious scheme to realize spin motive forces for neutral atoms. They show that atoms loaded in an optical trap and in the presence of a slowly varying time-dependent quadrupolar magnetic field experience a fictitious electromagnetic field in the laboratory frame. In the toroidal geometry proposed in their paper, the fictitious magnetic field is zero and the atoms experience only an azimuthal fictitious electric field in the lab frame, $E_{m_{F}}$ , which accelerates all atoms with a finite hyperfine spin projection $m_{F}$ along the torus (see Fig. 1).

The authors study specifically the case in which such a trap is loaded with a spinor Bose gas in the $F = 1$ hyperfine spin state (a gas of sodium atoms, for example), with equal densities of atoms in the states with hyperfine spin projection $m_{F} = 1$ and $m_{F} = 0$ . The former atoms are accelerated along the torus by the fictitious electric field $E_{m_{F}}$ , while the atoms in the $m_{F} = 0$ state do not couple to this field. However, they are accelerated indirectly by the spin drag mechanism stemming from the short-range atomic interactions between the two spin species. The key finding of their paper is that the rate of momentum transfer $ρ_{D}$ in this system increases as $T^{- 5 / 2}$ as temperature is lowered, at odds with what happens in Fermi systems, as discussed above. The reason for this dramatic difference is quantum statistics: Pauli blocking here is replaced by Bose enhancement. In other words, scattering to states already occupied by other bosons is enhanced rather than suppressed. This leads to a giant spin drag. Indeed, the estimated magnitude of the spin drag relaxation time $τ_{D}$ at a temperature of $400 nK$ is of the order of $τ_{D} \sim 0.1 s$ . Considering that the typical density $n$ of a cold atom ensemble is of the order of $10^{12} {cm}^{- 3}$ and using the atomic mass $M$ of sodium, one can estimate a transresistance $ρ_{D} = M / (n τ_{D} e^{2}) \sim 10^{- 5}$ $Ω m$ (see Ref. [17]), to be compared with the characteristic value of $10^{- 9}$ $Ω m$ for ordinary spin Coulomb drag in a bulk semiconductor [9].

Two other aspects distinguish this work from earlier work on electronic systems. Due to the absence of momentum relaxation, a true steady state can never be reached in the trap. Duine and Stoof thus carry out an analysis of spin dynamics as determined by the application of the azimuthal fictitious electric field for a finite period of time. Moreover, the increase of kinetic energy drives the system out of the regime of applicability of linear-response theory, which has been extensively used to describe Coulomb drag and spin drag in electronic systems. The authors are thus forced to go beyond the linear-response regime.

The work by Duine and Stoof lays a serious foundation for the observation of giant spin drag in an intrinsically ballistic regime. Some aspects of this work may be refined. It would be interesting, for example, to study the spin drag relaxation rate in the case of tight transverse confinement: in such a truly one-dimensional regime, many-body effects beyond the Fermi golden rule, i.e., multiple scattering events, might be relevant. A more extensive study of the experimental procedures needed to determine the relaxation rate is also necessary. Finally, it is easy to envision a wealth of possible future developments of this work. It is surely very tempting to investigate spin drag in cold Fermi gases close to a ferromagnetic critical point [18], as these systems parallel electron-hole bilayers close to exciton condensation, which exhibit anomalous Coulomb drag [19].

Acknowledgments

M.P.’s research in spin transport is currently funded by the European Community’s Seventh Framework Program (FP7/2007-2013) under grant agreement No. 215368. G.V. acknowledges support from DOE Grant No. DE-FG02-05ER46203.

References

M. B. Pogrebinskii, Sov. Phys. Semicond. 11, 372 (1977)
P. J. Price, Physica 117B, 750 (1983)
Lian Zheng and A. H. MacDonald, Phys. Rev. B 48, 8203 (1993)
A.-P. Jauho and H. Smith, Phys. Rev. B 47, 4420 (1993)
For a review see A. G. Rojo, J. Phys. Condens. Matter 11, R31 (1999)
T. J. Gramila, J. P. Eisenstein, A. H. MacDonald, L. N. Pfeiffer, and K. W. West, Phys. Rev. Lett. 66, 1216 (1991)
U. Sivan, P. M. Solomon, and H. Shtrikman, Phys. Rev. Lett. 68, 1196 (1992)
R. A. Duine and H. T. C. Stoof, Phys. Rev. Lett. 103, 170401 (2009)
I. D’Amico and G. Vignale, Phys. Rev. B 62, 4853 (2000); 65, 085109 (2002); 68,045307 (2003)
K. Flensberg, T. S. Jensen, and N. A. Mortensen, Phys. Rev. B 64, 245308 (2001)
C. P. Weber, N. Gedik, J. E. Moore, J. Orenstein, J. Stephens, and D. D. Awschalom, Nature 437, 1330 (2005)
M. Polini and G. Vignale, Phys. Rev. Lett. 98, 266403 (2007)
D. Rainis, M. Polini, M. P. Tosi, and G. Vignale, Phys. Rev. B 77, 035113 (2008)
Gao Xianlong, M. Polini, D. Rainis, M. P. Tosi, and G. Vignale, Phys. Rev. Lett. 101, 206402 (2008)
G. M. Bruun, A. Recati, C. J. Pethick, H. Smith, and S. Stringari, Phys. Rev. Lett. 100, 240406 (2008)
See, for example, G.F. Giuliani, and G. Vignale, Quantum Theory of the Electron Liquid (Cambridge University Press, Cambridge, 2005)[Amazon][WorldCat]
Note that the electric charge is used just to create an ohmic equivalent of the relaxation time $τ_{D}$ , i.e., to create the quantity $ρ_{D}$ with physical dimensions of resistance out of the other physical quantities $n$ , $M$ , and $τ_{D}$
G.-B. Jo, Y.-R. Lee, J.-H. Choi, C. A. Christensen, T. H. Kim, J. H. Thywissen, D. E. Pritchard, and W. Ketterle, Science 325, 1521 (2009)
G. Vignale and A. H. MacDonald, Phys. Rev. Lett. 76, 2786 (1996); A. F. Croxall, K. Das Gupta, C. A. Nicoll, M. Thangaraj, H. E. Beere, I. Farrer, D. A. Ritchie, and M. Pepper, ibid. 101, 246801 (2008); J. A. Seamons, C. P. Morath, J. L. Reno, and M. P. Lilly, 102, 026804 (2009)

About the Authors

Marco Polini is a CNR-INFM Researcher at the National Enterprise for nanoScience and nanoTechnology (NEST) in Pisa, Italy. He graduated in 1999 from the University of Pisa and received his Ph.D. in January 2003 from the Scuola Normale Superiore di Pisa. Immediately after, he went to work at the University of Texas at Austin as a visiting postdoctoral fellow until July 2003. In July 2003, he was hired at NEST as a tenure-track research scientist until December 2008, when he became permanent staff. Dr. Polini has mainly worked on two-dimensional electron liquids and ultracold atoms trapped in low-dimensional geometries, and he is a coauthor of over 60 publications. Since 2006 his work has mostly focused on the role of electron-electron interactions in single- and bi-layer graphene.

Giovanni Vignale is Curators’ Professor of Physics at the University of Missouri-Columbia. After graduating from the Scuola Normale Superiore in Pisa in 1979 and gaining his Ph.D. at Northwestern University in 1984, he carried out research at the Max-Planck-Institute for Solid State Research in Stuttgart, Germany, and Oak Ridge National Laboratory. He became a Fellow of the American Physical Society in 1997. Professor Vignale’s main areas of research are many-body theory and density-functional theory. He is the author of two books, Quantum Theory of the Electron Liquid and The Beautiful Invisible and has published almost 200 papers.