Observation of directed percolation—a class of nonequilibrium phase transitions

Haye Hinrichsen

Viewpoint

Observation of directed percolation—a class of nonequilibrium phase transitions

Fakultät für Physik und Astronomie, Universität Würzburg, 97074 Würzburg, Germany

November 16, 2009• Physics 2, 96

Directed percolation, a class of nonequilibrium phase transitions as prominent as the Ising model in equilibrium statistical mechanics, is realized experimentally for the first time, after more than fifty years of research. 

Figure caption — **Figure 1:** Illustration of directed percolation in $1 + 1$ dimensions: Bonds of a tilted square lattice are open (black lines) with probability $p$ and closed (no lines) otherwise. A preferred direction is introduced, which may be interpreted as time. Initially all sites are active (red dots). Activity percolates along the preferred direction through open bonds (red lines), activating nearest neighbors and giving rise to a certain spatiotemporal cluster of activity.

In statistical physics, a large number of theoretical studies are concerned with continuous phase transitions far from equilibrium [1]. Generically, the critical behavior near the transition is found to be universal, in the sense that apparently unrelated models may exhibit the same type of long-range behavior characterized by the same set of critical exponents and scaling functions. As in the equilibrium case, this allows one to categorize such transitions into universality classes determined by the symmetry properties of the model. However, nonequilibrium phase transitions are much more diverse than their equilibrium counterpart, since time is involved as an active degree of freedom, on equal footing with the spatial coordinates.

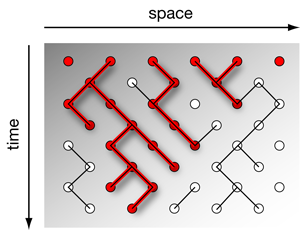
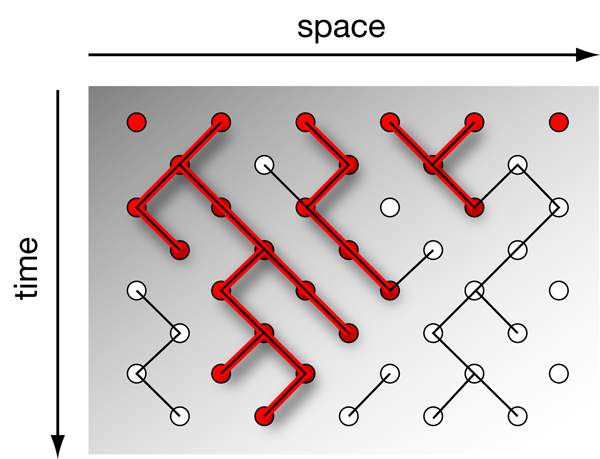
The best studied and probably simplest model with a nonequilibrium phase transition is directed percolation, which was introduced in 1957 by Broadbent and Hammersley [2] as a model for a porous medium in a gravitational field, an illustration of which can be seen in Fig.1. The pores of the medium are represented by the sites of a tilted square lattice, in which neighboring pores are connected by small channels that have a certain probability of being open or closed. When a liquid is poured onto the surface, it percolates downwards along the open channels, driven by gravity (red lines in the figure), and it turns out that there is a well-defined probability for the medium to become macroscopically permeable, at which point the system undergoes a continuous phase transition with a nontrivial critical behavior.

Another example of directed percolation behavior is the so-called contact process for epidemic spreading [3]. In this model the sites of a lattice represent “healthy” (inactive) and “infected” (active) individuals who spontaneously recover or infect nearest neighbors. Depending on the rates for infection and recovery, the infection may either spread over the whole system or disappear after some time. Once the infection becomes extinct the system enters a completely inactive configuration where the dynamics become trapped in a nonfluctuating so-called “absorbing state.” In this state all sites are inactive (healthy), meaning that the epidemic has completely disappeared. The system can enter this state, but cannot leave it.

Although there have been various attempts to find an actual example of directed percolation [4], none of the experiments showed clear and reproducible evidence of the critical behavior of this phase transition. This is remarked upon by Grassberger [5]: “…there is still no experiment where the critical behavior of DP was seen. This is a very strange situation in view of the vast and successive theoretical efforts made to understand it. Designing and performing such an experiment has thus top priority in my list of open problems.” Now, in a paper appearing in Physical Review E, Kazumasa Takeuchi, Masafumi Kuroda, Hugues Chaté, and Masaki Sano [6], of the University of Tokyo, Japan, and CEA-Saclay, France, follow their first report of directed percolation in liquid crystals [7] with a detailed discussion of the experiment and analysis that will allow their results to be tested against a long history of theoretical predictions. In these studies, they clearly observe directed percolation critical behavior.

The group’s experimental setup consists of a 12- $μ$ m-thick layer of nematic liquid crystals sandwiched between two glass plates that are covered by transparent electrodes, through which light is transmitted. A sufficiently high voltage applied at the electrodes causes a turbulent flow between the two plates due to the Carr-Helfrich instability. Above a certain threshold voltage, additional turbulent regimes emerge that exhibit spatiotemporally intermittent dynamics. These appear as gray spots. Within these spots, the excited turbulent state is topologically different from the surrounding one and can be detected by an increased absorption of light. The spots disappear spontaneously and also induce the creation of new spots nearby, thus spreading in just the same way as in a 2+1-dimensional contact process.

Unlike previous experimental attempts [4], the work by Takeuchi et al. reports measurements of as many as 12 critical exponents, including even nonstandard ones such as persistence exponents. All estimates are found to be in agreement with directed percolation and the expected scaling relations.

This impressive evidence for directed percolation is supported even further by a quantitative test of scaling functions. For example, according to the scaling theory of directed percolation the density of gray spots is expected to obey the scaling form $ρ (V, t) = t^{- α} R (t (V - V_{c}))^{ν_{t}}$ , where $α$ and $ν_{t}$ are numerically known critical exponents and $R$ is a scaling function. Scaling functions like $R$ are as universal and robust as critical exponents, and since functions carry much more information than a set of numbers, a quantitative comparison of scaling functions provides a much tougher test of universality than the comparison of critical exponents alone. Takeuchi et al. have tested various scaling functions, finding all of them in agreement with the corresponding numerical results. Given this impressive evidence of directed percolation critical behavior, one can consider this experiment as the first successful realization of directed percolation in nature.

Why is this experiment more successful than previous ones? On the one hand, timescales of milliseconds are much shorter than in other settings. To verify scaling laws, one has to average over many statistically independent realizations, i.e., repeat the experiment many times. If you try to realize directed percolation by artificial forest fires, each run takes hours. In the present case this is a matter of seconds, allowing one to obtain good statistical averages in a reasonably short time. Another fortunate circumstance for this experiment lies in the fact that “inactive” and ”active” patches of the system are both turbulent. The fully turbulent background dynamics provides the necessary randomness and suppresses long-range correlations. Apparently it also eliminates any kind of quenched randomness, which in other experimental setups is known to hide or even to destroy the transition. Either of these factors could be responsible for the success of this study, and further experimental effort is needed to clarify what role they play in this achievement. However, the demonstration of directed percolation opens up the possibility of investigating other universality classes using similar experimental methods.

References

For an introduction see, e.g., M. Henkel, H. Hinrichsen, and S. Lübeck, Non-equilibrium Phase Transitions (Springer, Dordrecht, 2008)[Amazon][WorldCat]
S. R. Broadbent and J. M. Hammersley, Proc. Camb. Phil. Soc. 53, 629 (1957)
T. E. Harris, Ann. Prob. 2, 969 (1974)
For a summary and see H. Hinrichsen, Braz. J. Phys. 30, 69 (2000)
P. Grassberger, in Nonlinearities in Complex Systems, edited by S. Puri and S. Dattagupta (Narosa, New Delhi, 1997)[Amazon][WorldCat]
K. A. Takeuchi, M. Kuroda, H. Chaté, and M. Sano, Phys. Rev. E 80, 051116 (2009)
K. A. Takeuchi, M. Kuroda, H. Chaté, and M. Sano, Phys. Rev. Lett. 99, 234503 (2007); 103, 089901 (2009)

About the Author

Haye Hinrichsen received his Ph.D. from the University of Bonn, Germany, in 1993. Since then he has held positions at the Free University of Berlin, the Weizmann Institute of Science, Israel, the Max Planck Institute for the Physics of Complex Systems in Dresden, and the Universities of Duisburg-Essen and Wuppertal, Germany. Since 2003 he has been Professor of Theoretical Physics at the University of Würzburg, Germany. His research is focused on phase transitions and critical phenomena in nonequilibrium statistical physics.