Staying or going? Chirality decides!

Edward  McCann

Viewpoint

Staying or going? Chirality decides!

Department of Physics, Lancaster University, Lancaster LA1 4YB, UK

November 23, 2009• Physics 2, 98

Due to unusual spinlike properties, electrons in graphene—despite scattering—exhibit a small increase in their conductivity.

Figure caption — **Figure 1:** (a) Two classical paths connecting arbitrary points A and B in a two-dimensional disordered conductor. (b) A pair of closed paths that contribute to the weak localization correction. (c) In a single scattering event, a long-range potential is unable to scatter chiral quasiparticles in the backwards direction (upper left) because it can’t reverse the pseudospin direction (black arrows), whereas scattering in the forwards or sideways direction (lower right) is allowed [15].

When an electronic device is cooled to low temperature, the wavelike nature of charge carriers becomes detectable through quantum interference effects. One example is weak localization, a small decrease in the conductivity of a disordered conductor [1,2]. Since interference depends on the quantum-mechanical phase of electronic waves, the experimental signature of weak localization has been used over the last thirty years to probe the nature of charge carriers and disorder in numerous conducting materials [3,4]. A new material to recently undergo such scrutiny is graphene [5], a one-atom-thick layer of carbon atoms. It has created a huge amount of interest, partly because electrons in it act like massless neutrinos. This behavior is manifest in a range of observed phenomena, including the integer quantum Hall effect [6–8], and it gave rise to the prediction of weak antilocalization in graphene [9], a small increase in the conductivity [2], rather than weak localization. So far, however, experiments have failed to clearly see this effect, reporting instead either weak localization or a suppression of it [10–13]. But now, writing in Physical Review Letters, Fedor Tikhonenko, Aleksey Kozikov, Alexander Savchenko, and Roman Gorbachev [14] at the University of Exeter, UK, demonstrate how to observe a transition from weak localization to antilocalization in graphene.

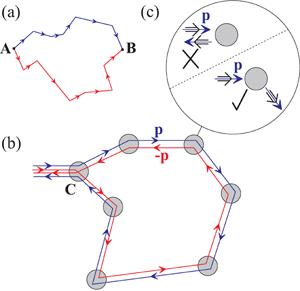
A qualitative picture of weak localization has been developed using Feynman’s formulation of quantum mechanics, in which the amplitude for propagation is given by a sum over classical paths, each path having its own amplitude and phase [3,4]. Typical classical paths connecting two points, A and B, are sketched in Fig. 1 (a) for a two-dimensional disordered conductor. Each path follows the random walk of an electron experiencing diffusive motion—a series of straight-line segments connecting each scattering event. The scattering is elastic, so that the phase acquired along any given path is well defined. However, for propagation from A to B, there are many different paths in addition to the two shown in Fig. 1 (a). Each has a different length and acquired phase, so that the sum over them involves many random phases. Interference between such paths averages to zero and electrical conductivity remains as described by the classical Drude model.

Interference effects become relevant for closed paths because two electrons may start from a given point, C, and travel in opposite directions, as illustrated in Fig. 1 (b). Two phases $ϑ_{↻}$ and $ϑ_{↺}$ acquired by the electrons as they propagate along the closed path in a clockwise and counterclockwise direction, respectively, are exactly equal. This results in constructive interference of the counterpropagating electrons when they return to the starting point C, which enhances the probability to backscatter and produces a decrease of conductivity [1]. Traversal of a closed loop in two directions may be viewed as motion of a particle and its time-reversed counterpart that traverse the path in opposite directions, indicating that their constructive interference is based on time reversal symmetry. A weak magnetic field perpendicular to the conductor violates time reversal symmetry and suppresses weak localization. This manifests in experiments as a negative magnetoresistance.

Weak localization relies on the phase coherence of electrons as they travel along closed paths. Inelastic scattering—caused by collisions with phonons or other electrons, for example—destroys phase information and sets the typical scale, the dephasing length, for suppression of the interference effect. Thus contributions to the constructive interference only come from return paths that are short enough (compared to the dephasing length) to remain phase coherent. Since the dephasing length tends to decrease with increasing temperature, observation of the effect usually requires low temperature (typically, a few tens of kelvin).

The above picture is strongly modified in graphene [5] because electrons in it possess an additional spinlike quantum number, known as pseudospin. It appears because the honeycomb lattice consists of two triangular sublattices, and two components of the electronic wave function on them are analogous to the two components of spin $1 / 2$ . An “up” pseudospin state would correspond to all the electronic density lying on one sublattice, “down” to all the density on the other, but since the density is shared equally between the two sublattices, the pseudospin is a linear combination of “up” and “down,” and it lies in the plane of the graphene sheet. Furthermore, quasiparticles in graphene are chiral, meaning that the orientation of the electron’s pseudospin is either parallel or antiparallel to the direction of its momentum.

A long-range potential, due, for example, to charges trapped in the substrate, is not able to differentiate between neighboring atoms and thus it does not affect the pseudospin. Owing to the conservation of pseudospin, such a potential is unable to scatter chiral quasiparticles in the backwards direction [15], Fig. 1 (c), and this suppression of backscattering is associated with weak antilocalization of electrons in graphene [9]. As electrons propagate around closed paths, Fig. 1 (b), the pseudospin remains parallel to the momentum. For a clockwise path [blue line in Fig. 1 (b)], the pseudospin rotates by an angle of $- π$ in the graphene plane; for an anticlockwise path (red line), the angle of pseudospin rotation is $π$ . The difference in the angle of rotation of the pseudospin for the counterpropagating paths is then $2 π$ . In analogy to the rotation of a spin- $1 / 2$ fermion, for which a rotation by $2 π$ doesn’t return the wave function to its original state, net rotation of the pseudospin by $2 π$ induces a phase difference of $π$ between the counterpropagating paths. The returning electrons are now out of phase. This leads to destructive interference that suppresses backscattering, producing an increase of conductivity called weak antilocalization [2,9]. Suppression of antilocalization by a perpendicular magnetic field will then be seen as positive magnetoresistance.

Graphene has two copies—known as valleys—of the gapless Dirac-like spectrum. In the absence of intervalley scattering, the interference of counterpropagating electrons from the same valley is sensitive to intravalley symmetry-breaking perturbations that affect the pseudospin. Counterpropagating electrons accumulate different phases, suppressing any (negative or positive) magnetoresistance effect. Intervalley scattering, on the other hand, allows the counterpropagating electrons to occupy different valleys [16,17]. As the two valleys have opposite chirality, the phases acquired by the electron and its time-reversed partner around a closed loop are equal, resulting in constructive interference and a restoration of the weak localization effect [10–13,16,17].

The tendency of symmetry-breaking perturbations, either intra- or intervalley, to destroy weak antilocalization suggests that it shows up only in relatively clean samples. Not only did Tikhonenko and coauthors [14] improve sample quality, they were also able to tune the ratio of the dephasing length to the symmetry-breaking length. They did this by (a) increasing temperature to reduce the dephasing length and (b) employing an applied gate voltage to decrease carrier density— thus increasing the intervalley scattering length. In this work they exploited behavior established by them in earlier experiments [13].

At low temperature, when the dephasing length exceeds the symmetry-breaking length, weak localization is observed, as in previous experiments [10–13]. However, by decreasing the ratio of the dephasing length to the symmetry-breaking length, it was possible to enter the regime when decoherence suppresses the influence of symmetry-breaking perturbations. In this case, Tikhonenko et al. observe positive magnetoresistance, a clear signature of weak antilocalization arising from phase-coherent paths short enough to preserve the chiral nature of counterpropagating electrons. Surprisingly, they find that weak antilocalization persists up to a relatively high temperature of around $200 K$ , owing to weak electron-phonon scattering in graphene, so that the main source of dephasing over a broad range of temperature remains electron-electron scattering.

The observation of weak antilocalization in graphene arises from a phase difference of $π$ acquired by counterpropagating chiral electrons. One does not expect this in bilayer graphene where the chirality of low-energy quasiparticles is different [8,18]. In bilayers, pseudospin is linked to the direction of momentum, but turns twice as quickly as momentum does. The acquired phase difference of counterpropagating chiral electrons would be a multiple of $π$ , resulting in weak localization [12,16,19]. So far, the story of weak localization in graphene involves the interplay of additional spinlike quantum numbers, related to lattice and valley degrees of freedom, but not electronic spin itself. Spin-orbit coupling may be an alternative way to induce weak antilocalization in graphene and bilayer graphene, as in conventional conductors [2,3], but its observation is likely to be challenging in view of the predicted weakness [20] of the spin-orbit interaction in graphene.

References

B. L. Altshuler, D. Khmelnitski, A. I. Larkin, and P. A. Lee, Phys. Rev. B 22, 5142 (1980)
S. Hikami, A. I. Larkin, and N. Nagaosa, Progr. Theor. Phys. 63, 707 (1980)
G. Bergmann, Phys. Rep. 107, 1 (1984)
B. L. Altshuler and P. A. Lee, Physics Today 41 No. 12, 36 (1988)
K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, and A. A. Firsov, Science 306, 666 (2004)
K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, and A. A. Firsov, Nature 438, 197 (2005)
Y. B. Zhang, Y. W. Tan, H. L. Stormer, and P. Kim, Nature 438, 201 (2005)
K. S. Novoselov, E. McCann, S. V. Morozov, V. I. Fal’ko, M. I. Katsnelson, U. Zeitler, D. Jiang, F. Schedin, and A. K. Geim, Nature Phys. 2, 177 (2006)
H. Suzuura and T. Ando, Phys. Rev. Lett. 89, 266603 (2002)
S. V. Morozov, K. S. Novoselov, M. I. Katsnelson, F. Schedin F, L. A. Ponomarenko, D. Jiang, and A. K. Geim, Phys. Rev. Lett. 97, 016801 (2006)
X. Wu, X. Li, Z. Song, C. Berger, and W. A. de Heer, Phys. Rev. Lett. 98, 136801 (2007)
R. V. Gorbachev, F. V. Tikhonenko, A. S. Mayorov, D. W. Horsell, and A. K. Savchenko, Phys. Rev. Lett. 98, 176805 (2007)
F. V. Tikhonenko, D. W. Horsell, R. V. Gorbachev, and A. K. Savchenko, Phys. Rev. Lett. 100, 056802 (2008)
F. V. Tikhonenko, A. A. Kozikov, A. K. Savchenko, and R. V. Gorbachev, Phys. Rev. Lett. 103, 226801 (2009)
T. Ando, T. Nakanishi, and R. Saito, J. Phys. Soc. Jpn. 67, 2857 (1998)
A. F. Morpurgo and F. Guinea, Phys. Rev. Lett. 97 196804 (2006)
E. McCann, K. Kechedzhi, V. I. Fal’ko, H. Suzuura, T. Ando, and B. L. Altshuler, Phys. Rev. Lett. 97, 146805 (2006)
E. McCann and V. I. Fal’ko, Phys. Rev. Lett. 96 086805 (2006)
K. Kechedzhi, V. I. Falko, E. McCann, and B. L. Altshuler, Phys. Rev. Lett. 98, 176806 (2007)
D. Huertas-Hernando, F. Guinea, and A. Brataas, Phys. Rev. B 74, 155426 (2006)

About the Author

Edward McCann received his Ph.D. from the University of Birmingham, UK, for theoretical work on mesoscopic fluctuations in disordered conductors. He was a postdoctoral researcher at the Max-Planck-Institut für Physik komplexer Systeme, Dresden, Germany, before moving to Lancaster University, UK, initially as an EPSRC Junior Research Fellow and later as a Lecturer in Condensed Matter Physics. His recent research has focused on the electronic properties of graphene, a single-atom-thick layer of carbon atoms, and of few-layer graphene films.