Observing the dance of a vortex−antivortex pair, step by step

Peter Engels

Viewpoint

Observing the dance of a vortex−antivortex pair, step by step

Department of Physics and Astronomy, Washington State University, Pullman, WA 99163, USA

April 19, 2010• Physics 3, 33

New experiments create pairs of vortices of opposite circulation by forcing a Bose-Einstein condensate to flow past an obstacle.

Figure caption — **Figure 1:** (Top) Generation of a vortex dipole by moving a focused laser beam (red) through a BEC (blue disk). (Bottom) The motion of a vortex dipole can be understood by considering an analogy to a classical smoke ring (cyan) that propels itself forward because of Helmholtz’s vortex law.

The investigation of vortices in superfluids is a fascinating and active line of research that, by now, has a history spanning over half a century. Starting from the first observations of quantized circulation in liquid helium in the 1950s [1], the field has undergone tremendous progress. Nowadays, dilute-gas Bose-Einstein condensates (BECs) provide a powerful tool with which vortex research can be pushed into new regimes, and several hallmark results have been obtained, reaching from interferometric measurements of the quantum mechanical phase of individual vortices to the direct imaging of large vortex lattices containing over $300$ vortices in a regular array [2]. Now Tyler Neely and collaborators at the University of Arizona in the US, the Jack Dodd Center for Quantum Technology in New Zealand, and the University of Queensland in Australia [3] are adding another chapter to the story of vortices in superfluids. They have succeeded in creating vortex dipoles, consisting of a vortex paired with an antivortex, in such a controlled way that the dynamics can be studied in detail. An antivortex differs from a vortex only in the orientation of the circular fluid flow. When a vortex and an antivortex meet in a harmonic trap (such as the one holding the BEC in the Neely experiment), they can pair up to form a vortex dipole and then perform an enchanting dance that has now been imaged for the first time. The long lifetime of the vortex dipole and the stability of the observed dynamics are quite intriguing, indicating that such dynamics may also play a key role in other situations where vortices and antivortices emerge, e.g., superfluid turbulence. In another recent paper, periodic streets of vortex pairs in BECs have been studied numerically by Sasaki et al. [4]. Vortex physics also exists in systems as diverse as superfluid Fermi systems, magnetic flux lines in superconductors, and neutron stars. Thus a precise understanding of vortex dynamics is highly desirable, and BECs can lead the way in elucidating the physics of vortices in a well-controlled environment.

Vortices emerge when a superfluid is subjected to rotation. At first sight, it may seem surprising that something as apparently simple as inducing rotation would lead to interesting dynamics. To see why this is the case, recall that the velocity of a superfluid is proportional to the gradient of the phase of the underlying macroscopic wave function. The curl of a gradient field is generally zero and thus the flow is irrotational. Consequently, interesting dynamics are bound to occur when the irrotational fluid is subjected to rotation. The outcome is best understood by first considering the flow of water in a sink after the drain plug has been pulled. The water starts rushing down the drain and after a short while forms a rather stable vortex above the drain. If a little paper boat is placed into the swirling water, the boat spirals around the drain in such a way that its bow always points into the same direction. This is due to the fact that conservation of angular momentum of the water spiraling towards the drain leads to a $1 / r$ dependence of the fluid velocity on the distance $r$ from the drain, “compensating” for the rotation of the fluid around the drain. So the flow is irrotational, even though the stream is clearly curved. If, on the other hand, the boat is placed such that it stretches across the central eddy, then it is found to rapidly spin around its vertical axis. For a rotating superfluid, the situation is quite similar: based on the requirement of a uniquely valued wave function, similar $1 / r$ dependence can be derived. Vorticity, defined as the curl of the velocity field, is concentrated in the vortex core where the superfluid density goes to zero. Everywhere else the fluid is irrotational, as expected for a superfluid.

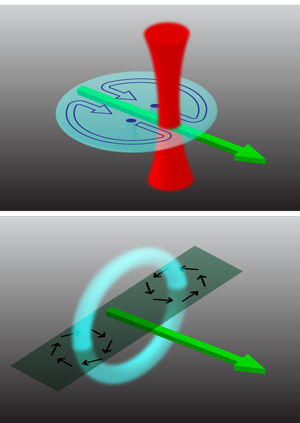
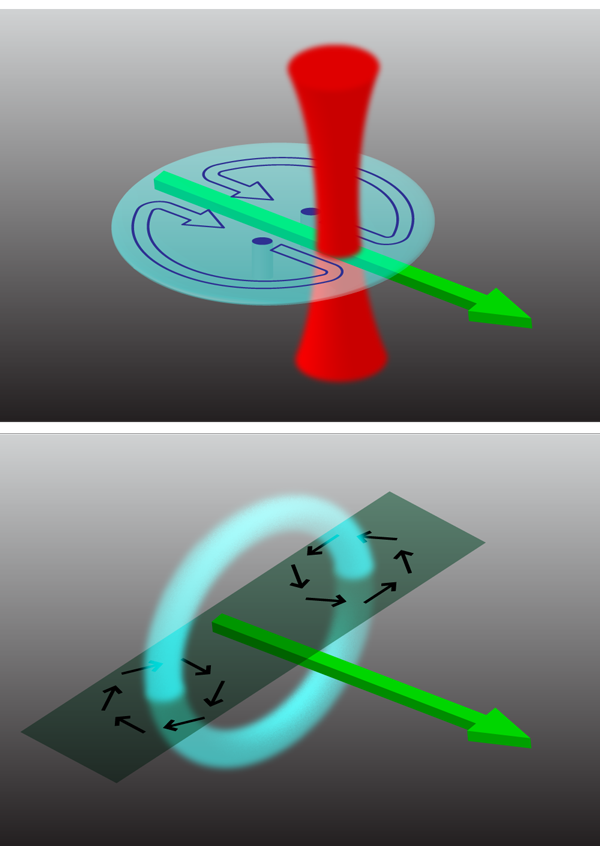
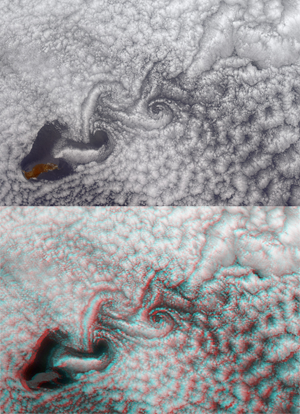
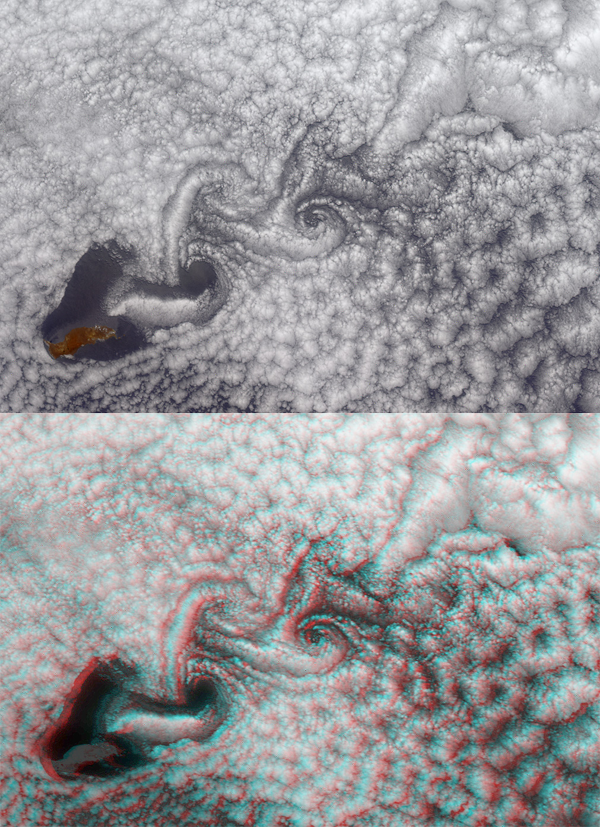
Over the past decade, many experimental techniques have been devised and implemented to generate vorticity in BECs [2]. Most of these techniques either create vortices that all spin in the same way (i.e., no antivortices), or offer little to no control over the vortex/antivortex pairs that they may create. The technique used by Neely et al. consists of dragging a small cylindrical obstacle through the BEC (Fig. 1, top panel). The obstacle is experimentally realized by a focused laser beam that exerts a repulsive dipole force on the atoms. In the wake of the obstacle, vortices and antivortices can be generated. The effect is familiar, for example, from the von Karman vortex street of clouds sometimes observed behind islands in the ocean (see Fig. 2). Vortices generated behind obstacles also influence the design of car antennas and are said to be responsible for the collapse of cooling towers at the Ferrybridge power station in the 1960s [5]. The fact that this mechanism also works for superfluids was demonstrated using computer simulations in 1992 [6] and in a BEC experiment in 2001 [7]. Neely et al. have now perfected this technique to such a degree that, for the first time, the dance of a vortex and an antivortex in a harmonic trap can be followed in detail.

To understand this, first consider a classical vortex ring such as a smoke ring that can be emitted by smokers and volcanoes alike (Fig. 1, bottom panel). Vortex rings are also believed to occur inside a pumping heart [8] and exist in superfluids as well [9]. One of the familiar features of a smoke ring is that it does not stand still but travels forward, in a direction pointing along its symmetry axis. This is expressed in the Helmholtz vortex law, which says that a vortex floats along with the local fluid velocity. For a vortex ring, this means that any small segment of the ring moves along with the fluid velocity at its location generated by the rest of the ring. In this way, the vortex ring propels itself forward.

A conceptual connection between the familiar vortex ring and the motion of the vortex dipole in the Neely experiment can be made by considering the oblate BEC as essentially a plane cutting horizontally through the vortex ring along its symmetry axis. At the intersection, a vortex and an antivortex arise (see Fig. 1, bottom panel). This vortex dipole moves along a straight line through the trap in much the same way as the classical vortex ring propels itself forward. The finite extent of the BEC and the presence of the harmonic trapping potential complicate the situation. When approaching the end of the cloud, the vortex/antivortex pair separates. This is reminiscent of the spreading of a classical vortex ring hitting a wall. The vortex and antivortex then precess in opposite directions along the edge of the BEC until they meet again on the other side, pairing up and starting the next cycle of their dance. For an individual vortex, such precession has been observed before [10] and can intuitively be understood as follows: the inhomogeneous density distribution of a harmonically trapped BEC leads to a radially directed buoyancy force on a vortex. Since the vortex is a rotating object, it responds to a radial force by performing azimuthal motion. This is related to the Magnus effect in classical fluids, which affects the motion of spinning balls in many ball games, and also led to the idea of the Flettner boat, a sailing boat that replaces conventional sails by spinning cylinders.

One of the beautiful aspects of the new experiments is the repeatability with which vortex dipoles can now be produced. Since vortex cores are usually below the optical imaging resolution of the detection system, observing them requires turning the trap off and letting the BEC expand for a few milliseconds before imaging the cloud. This type of detection is necessarily destructive, and obtaining a coherent sequence of images requires a sufficient amount of repeatability over many experimental runs. In the experiment, the motion is followed over several cycles in the harmonic trap, and excellent agreement is found with numerical simulations. A second intriguing aspect is the long lifetimes of the dipoles: even though the vortex and antivortex come very close during the straight parts of their motion, they are not observed to annihilate right away. This surprising stability is explained by the oblate geometry of the BEC: the vortex and antivortex lines in the experiment are very short and therefore fairly resistant to bending. The vortex line does not bend, split, and reconnect with the antivortex line, and thus is fairly stable. Finally, adding even more players to the field, Neely et al. have repeated their experiment with an increased speed of their obstacle, thus creating aggregates of up to three vortices and three antivortices. Interestingly, novel dynamics is observed: the vortices form a group that moves together, and so do the antivortices. These two groups then form the two parts of the dipole.

The research in vortices is still going strong even though it has been over $50$ years since the first prediction and detection of a vortex in a superfluid. The observed dance of a vortex dipole is the newest highlight in a line of research that, over the years, has taught us much about the peculiar phenomenon of superfluidity, and even more may be just around the corner. One can speculate that with controlled generation of a vortex and antivortex now achieved, it may just be a matter of time until controlled reconnections between vortex lines can be observed in detail. This would be yet another milestone on the path towards an understanding of quantum turbulence, a hot topic currently entering the BEC scene [11].

References

See, e.g., R. J. Donnelly, Quantized vortices in Helium II (Cambridge University Press, Cambridge, 1991)[Amazon][WorldCat]
See, e.g., P. G. Kevrekidis et al., Emergent Nonlinear Phenomena in Bose-Einstein Condensates (Springer, Berlin, 2008)[Amazon][WorldCat]
T. W. Neely, E. C. Samson, A. S. Bradley, M. J. Davis, and B. P. Anderson, Phys. Rev. Lett. 104, 160401 (2010)
K. Sasaki, N. Suzuki, and H. Saito, Phys. Rev. Lett. 104, 150404 (2010)
See, e.g., Neil Schlager, When Technology Fails: Significant Technological Disasters, Accidents, and Failures of the Twentieth Century (Gale Research Inc., Detroit, 1994)[Amazon][WorldCat]
T. Frisch, Y. Pomeau, and S. Rica, Phys. Rev. Lett. 69, 1644 (1992)
S. Inouye et al., Phys. Rev. Lett. 87, 080402 (2001)
B. J. Bellhouse, Cardiovascular Research 6, 199 (1972)
G. W. Rayfield and F. Reif, Phys. Rev. 136, A1194 (1964)
B. P. Anderson, P. C. Haljan, C. E. Wieman, and E. A. Cornell, Phys. Rev. Lett. 85, 2857 (2000)
E. A. L. Henn, J. A. Seman, G. Roati, K. M. F. Magalhaes, and V. S. Bagnato, J. Low. Temp. Phys. 158, 435 (2010)

About the Author

Peter Engels studied physics at the University of Bonn, Germany. After a stay at Princeton University as a visiting graduate student, he received his Ph.D. from the University of Hanover, Germany. In his postdoctoral research at JILA / University of Colorado, he investigated the physics of vortex lattices in BECs. He currently holds an Associate Professor position at Washington State University where he conducts experiments studying the dynamics of BECs and quantum degenerate Fermi gases.