Cellular aggregates under pressure

Gabor Forgacs; Ioan Kosztin

Viewpoint

Cellular aggregates under pressure

Department of Physics and Astronomy, University of Missouri, Columbia, MO 65211, USA

May 24, 2010• Physics 3, 43

Researchers develop a new approach to measuring the viscoelastic properties of multicellular aggregates by using a micropipette aspiration technique.

Figure caption — **Figure 1:** Scanning electron microscopy images of $300$ -micron-diameter multicellular aggregates of (A) human umbilical smooth muscle cells, and (B) N-cadherin transfected Chinese hamster ovary cells. The aggregate with larger surface tension (A) displays a smooth surface, while the one with smaller surface tension (B) has a berrylike surface.

It is widely accepted by now that the mechanical characteristics of cells and tissues play an important role in numerous biological processes, such as early morphogenesis [1,2], signal transduction [3], cell adhesion [4], and even stem cell differentiation [5,6]. In particular, it was suggested and experimentally demonstrated that a number of phenomena in embryonic tissues can be interpreted through their viscoelastic properties [7]. Tissue mechanical properties have often been quantified by measurements using spherical aggregates of cells (as models of tissues) and parallel-plate tensiometry [8]. In this technique the aggregates are exposed to a fixed strain by compression between the plates and the viscoelastic parameters such as surface tension ( $γ$ ), elastic constant ( $E$ ), and viscosity ( $η$ ) are determined from the relaxation of the compressive force (i.e., stress) to equilibrium. In a work published in Physical Review Letters [9], Karine Guevorkian and collaborators from CNRS-Institut Curie and Ecole Polytechnique, both in France, and McMaster University, Canada, use, for the first time, micropipette aspiration—a method normally applied to individual cells—to test the mechanical behavior of multicellular spheroids and to determine $γ$ , $E$ , and $η$ .

In this approach, the spheroid is aspirated into a pipette of much smaller diameter than that of the spheroid, with a constant suction pressure $Δ P$ . Thus the approach is complementary to the parallel-plate method, as now the applied stress is constant and the viscoelastic properties of the tissue are deduced from the variation of the strain (i.e., the change in length of the cellular material as it flows inside the pipette). As tissues are complex materials with complex constitutive equations, it is not obvious that the two methods should lead to the same set of viscoelastic parameters. Indeed, Guevorkian et al. find that the surface tension of cell aggregates composed of a murine sarcome cell line (transfected with the cell adhesion molecule E-cadherin) depends on $Δ P$ , whereas in parallel-plate experiments, no dependence of the surface tension on the compressive force was observed.

As shown in Ref. [9], cells aspirated with force $f_{a}$ , imposed by $Δ P$ , reach steady inflow into the pipette with velocity $v_{a} = C (Δ P - Δ P_{c})$ . Here, $C = R_{p} / 3 π η$ , $R_{p}$ is the radius of the pipette, and $Δ P_{c} \approx 2 γ / R_{p}$ is the critical (Laplace) pressure, at which flow stops (Fig. 2 in Ref. [9]). The above analytic expression for the aspiration velocity $v_{a}$ is obtained by balancing the aspiration force $f_{a} = π R_{p}^{2} (Δ P - Δ P_{c})$ , with the resistive viscous force $f_{v} = 3 π^{2} η R_{p} v_{a}$ . Aspiration is followed by retraction (upon setting $Δ P = 0$ ), leading to steady outflow from the pipette with $v_{r} = C Δ P_{c}$ . The measurable quantities $v_{a}$ , $v_{r}$ , and $Δ P$ are used to determine $γ$ and $η$ , through $C$ and $Δ P_{c}$ . Assuming that the latter parameters are the same in the aspiration and retraction phases, $Δ P_{c} = Δ P v_{r} / (v_{r} + v_{a})$ and $C = (v_{a} + v_{r}) / Δ P$ . The new finding in the work is that $v_{r}$ , and therefore $Δ P_{c}$ and $γ$ , depend significantly on $Δ P$ . (Unfortunately, $v_{a} + v_{r}$ vs $Δ P$ is not shown in Ref. [9], so one can only assume that this relationship was found to be linear, thus implying that $C \sim 1 / η$ is indeed independent of $Δ P$ .)

The $Δ P$ dependence of $v_{r}$ means that despite the fact that during retraction no external pressure is imposed on the system, the cells remember what the aspiration pressure was when they were moving into the pipette under $Δ P \neq 0$ . The authors interpret this result as an active cellular response to mechanical force leading to the remodeling of the cytoskeleton. This is an appealing explanation and consistent with other findings on the effect of mechanical forces on cells [10].

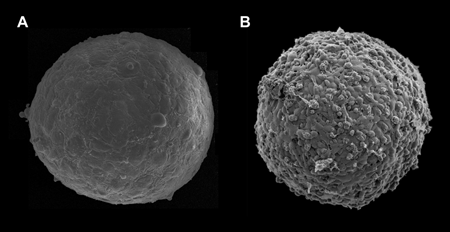
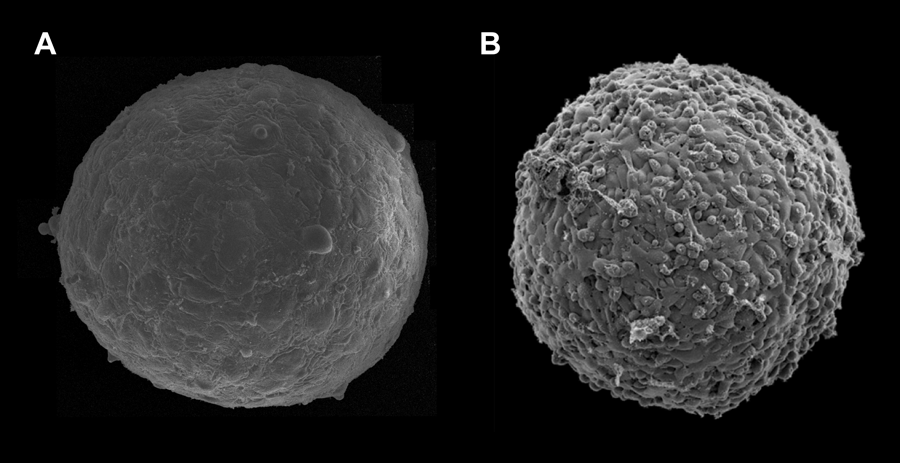
The work of Guevorkian et al. represents an important contribution to the field of tissue mechanics. However, the application of the micropipette aspiration technique to cellular aggregates raises several questions. First, most likely it is not applicable to weakly adhesive cells. (It would be useful to know how strong the adhesion between the E-cadherin transfected murine sarcoma cells is, in comparison to other cell types used to measure surface tension). Figure 1 shows the surface of $300$ -micron-diameter aggregates composed of human umbilical smooth muscle cells (HUSMC) (Fig. 1, A) and N-cadherin transfected Chinese hamster ovary (CHO) cells (Fig. 1, B), with respective surface tensions of $279 mN / m$ and $23 mN / m$ (as measured with parallel-plate tensiometer [11] and respective cell numbers of $8, 000$ and $12, 000$ ). The aggregate of higher tension displays a smooth and uniform morphology, while the aggregate of lower tension shows a berrylike surface. The differing morphologies reflect differential adhesion between the respective cells, with adhesion between CHO cells being significantly weaker than between HUSMC. As aspiration stretches the adhesive bonds between cells, at sufficiently weak adhesion and strong aspiration, the method may simply separate cells from one another.

Another problem arises from the finite number of cells aspirated into the pipette. For a $400$ micron aggregate and a $2 R_{p} = 70$ -micron-diameter pipette, there are about $12$ cells within the pipette’s cross sectional area (we assume the linear dimension of a murine sarcoma cell to be around $20$ micron). Thus the quantity $γ$ , measured by Guevorkian et al. reflects the properties of a small number of cells rather than those of the entire aggregate. Therefore, despite the fact that their measured surface tension has the same order of magnitude as that measured by other methods where the entire aggregate is probed (parallel-plate tensiometry [8,11], centrifugation [12]), it is not clear what $γ$ really means. Furthermore, surface tension is a strictly equilibrium quantity, but here, $γ$ is obtained from kinetic measurements. (Given that both $v_{a}$ and $v_{r}$ are small, the system most probably can be regarded as being in quasi-equilibrium, thus $γ$ is well defined.) Finally, it is somewhat puzzling that while $γ$ depends on $Δ P$ the viscosity $η$ of the cellular assembly in the pipette appears to be independent of $Δ P$ .

If the authors are right and indeed the cellular system has memory of the magnitude of the aspiration pressure when it retracts (when $Δ P = 0$ ) and it is this memory that causes $γ$ to depend on $Δ P$ , one would expect to see a similar effect in the compression experiments upon the variation of the compressive pressure. However, tissue surface tension measured by compressive tensiometry was found to be independent of the compressive pressure [11]. What may cause this discrepancy? It may result from the difference between the magnitudes of the applied aspiration and compressive pressures. At a sufficiently large pressure, it is probably not surprising that indeed the cellular system reorganizes. However, we find the aspiration pressures applied by Guevorkian et al. and the compressive pressures to be of the same order of magnitude. On the other hand, the aspiration pressure is applied effectively to a much smaller number of cells than the compressive pressure. If it is indeed the number of relevant cells that is responsible for the observed variation of $γ$ on $Δ P$ , then the question of what is the meaning of the measured surface tension remains to be answered. This could be accomplished by measuring the surface tension of aggregates of the murine sarcoma cells with compression tensiometry and to compare it with $γ (Δ P = 0)$ , as extrapolated from the values obtained using the micropipette aspiration technique.

References

D. E. Ingber, Int. J. Dev. Biol. 50, 255 (2006)
R. Keller, L. A. Davidson, and D. R. Shook, Differentiation 71, 171 (2003)
D. J. Tschumperlin, G. D. I. V. Maly, T. Kikuchi, L. H. Laiho, A. K. McVittie, K. J. Haley, C. M. Lilly, P. T. C. So, D. A. Lauffenburger, R. D. Kamm, and J. M. Drazen, Nature 429, 83 (2004)
J. Schmitz, and K-E. Gottschalk, Soft Matter 4, 1373 (2008)
A. J. Engler, S. Sen, H. L. Sweeney, and D. E. Discher, Cell 126, 677 (2006)
F. Chowdhury, S. Na, D. Li, Y-C. Poh, T. S. Tanaka, F. Wang, and N. Wang, Nature Mater. 9, 82 (2009)
G. Forgacs and S. Newman, Biological physics of the developing embryo (Cambridge University Press, Cambridge, 2005)[Amazon][WorldCat]
R. A. Foty, C. M. Pfleger, G. Forgacs, and M. S. Steinberg, Development 122, 1611 (1996)
K. Guevorkian, M-J. Colbert, M. Durth, S. Dufour, and F. Brochard-Wyart, Phys. Rev. Lett. 104, 218101 (2010)
B. J. Damon, N. Mezentseva, J. S. Kumaratilake, G. Forgacs, and S. A. Newman, Dev. Biol. 321, 319 (2008)
C. Norotte, F. Marga, A. Neagu, I. Kosztin, and G. Forgacs, Euro. Phys. Lett. 81, 46003 (2008)
A. Kalantarian, H. Ninomiya, S. M. I. Saad, R. David, R.Winklbauer and A. W. Neumann, Biophys. J. 96, 1606 (2009)

About the Authors

Gabor Forgacs is George H. Vineyard Professor of Biophysics at the University of Missouri. He received his Ph.D. in theoretical physics from the Roland Eötvös University, Budapest, Hungary. His present research interest is in the physical mechanisms acting in early embryonic development. He is applying these mechanisms to engineering and building living structures of prescribed shape and functionality by bioprinting.

Ioan Kosztin is an Associate Professor of Biological Physics at the University of Missouri. He received his Ph.D. in theoretical condensed matter physics from the University of Illinois at Urbana-Champaign. His current research interest is to develop and apply theoretical and computational models for investigating different aspects of the dynamics of biomolecular complexes and of multicellular aggregates.