A not-so-steady state

Carsten A. Ullrich

Viewpoint

A not-so-steady state

Department of Physics and Astronomy, University of Missouri, Columbia, MO 65211, USA

June 7, 2010• Physics 3, 47

Theory that takes into account the time-dependent nature of electronic transport through a quantum dot reveals fluctuations that could affect rapid switching of nanoscale electronic devices.

Figure caption — **Figure 1:** Steady-state picture of Coulomb blockade in a nanoscale tunneling junction in which a quantum dot is weakly connected to two leads. Electrons can tunnel only if the bias voltage $V$ is large enough to line up the chemical potential of the left lead ( $μ_{L}$ ) and an empty level. Otherwise the access is blocked due to the Coulomb repulsion caused by the filled $N$ -electron level.

When roads are clear, traffic proceeds as a continuous flow of cars; if the road is blocked, everything comes to a standstill. However, anyone stuck in the office rush knows life is more complex—traffic tends to move in waves, often slowing down to an annoying stop-and-go. Traffic congestion also makes life difficult for electrons in nanodevices. We tend to think of charge carriers as experiencing a controlled flow, reaching steady state when the gates are opened and current is on. Now, in a study published in Physical Review Letters, a team of scientists from four European countries point to the subtle but significant deviations from steady-state behavior that appear if one looks at the time dependence of electrons traversing a nanoscale junction. Stefan Kurth at Universidad del País Vasco in San Sebastián, Spain, and colleagues in Italy, Sweden, and Germany predict that, on a femtosecond time scale, the current in a quantum dot junction is not in a steady state, as often assumed, but rather oscillates [1]. The amplitude of this oscillation depends on how fast the bias voltage across the dot is switched on, suggesting the importance of initial conditions in determining how a single-electron device will perform. Their paper recasts nanoscale transport as an intrinsically dynamic phenomenon, which has important practical implications for understanding and designing ultrafast nanoelectronic devices.

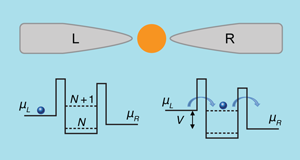
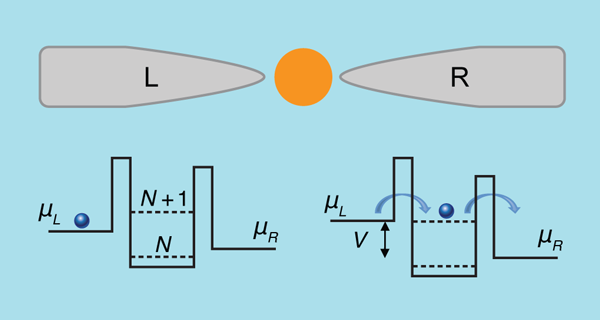
The charge transport through a quantum dot under weak bias and weakly coupled (by tunneling barriers) to a left and right lead (Fig. 1) is dominated by Coulomb blockade, where an electron already present on the dot prevents further electrons from tunneling in, unless the bias is significantly increased to supply the necessary charging energy. The central region of this system, consisting of the dot and the tunneling barriers, has a capacitance $C$ . The electrostatic energy of a charge $Q$ sitting on the dot is given by $Q^{2} / 2 C$ . To bring in an extra electron, the Coulomb repulsion due to the charge already present needs to be overcome, and for this to happen, the bias voltage ( $V$ ) must increase by $e / 2 C$ . The chemical potential of the left lead, $μ_{L}$ , and the empty $(N + 1)$ level then line up and an electron can tunnel in. For all bias voltages below this limit, no current flows and the access to the dot is blocked—an extremely non-Ohmic nanoscale electronic device.

In this simple and well-established scenario of nanoscale transport [2], the Coulomb blockade regime is a steady nonequilibrium state of the system where the current is zero. Theorists who want to go beyond this simple model face several challenges: Coulomb blockade is intrinsically a many-body phenomenon in which a full treatment of electron-electron interaction effects is vital. Furthermore, the charges sitting on the central dot are not in equilibrium with the rest of the system and have to be forced to remain there by balancing the external bias and the internal Coulomb repulsion.

In recent years, a “standard model” has emerged for calculating transport characteristics of quantum dots, molecular junctions, and other nanodevices [3]. One first determines the electronic level structure in the central region (the “dot” in Fig. 1) using density-functional theory (DFT) and then finds the total current through the device with the so-called Landauer formula, which integrates over the electron distribution in the leads weighted by their tunneling transmission probabilities. In their work, Kurth et al. critically reexamine a key assumption of this Landauer-DFT approach, namely that the transport through the device can be treated as a steady state. By adopting a time-resolved view of how electrons interact on the dot, they show that this assumption may often not be correct.

Systems of interacting electrons—atoms, molecules, or solids—are characterized by their quantum mechanical wave functions, which are formally obtained from the many-body Schrödinger equation. The core tenet of DFT is that all physical observables in a system of interacting electrons can be expressed by the electronic ground-state density (the number of electrons per volume). To obtain this density, one uses a trick known as the Kohn-Sham approach: rather than dealing with $N$ interacting electrons in some external potential, one gets the same density from a noninteracting system in an effective local single-particle potential that is determined self-consistently [4].

All complicated many-body effects are hidden in a part of this effective potential known as the “exchange-correlation potential.” There isn’t an exact expression for the exchange-correlation potential, but we know many of its properties and have a pretty good idea how to approximate it to obtain accurate electronic structures.

To describe Coulomb blockade in nanoscale transport it is particularly important to ensure the principle of charge quantization: in a steady state, the central dot should be occupied only by integer multiples of the electron charge. To guarantee this in a DFT calculation, the whole burden rests on a subtle correlation effect known as the “derivative discontinuity.” This means that the effective potential an electron experiences on the dot jumps by a constant when the number of electrons passes through an integer value [5]. Few existing approximations for the exchange-correlation potential have this property.

However, there is another dimension to this story. Nanoscale transport is a nonequilibrium phenomenon—but DFT is only a ground-state theory! This means that the proper formal framework in which to describe Coulomb blockade and other transport properties is the time-dependent version of DFT (known as TDDFT) [6], which, in principle, yields the exact time evolution of any interacting system. Time-dependent DFT has proven successful for calculating molecular excitation spectra. In contrast, the theory has been applied to only a few problems in transport [3].

Kurth et al.’s work is groundbreaking because it is the first time-dependent DFT study of transport through a nanoscale junction that incorporates charge quantization (the derivative discontinuity) into the effective interaction between the electrons on the quantum dot. This opens the possibility to study Coulomb blockade in real time and observe how electrons hop on and off the central dot, and block or grant access to additional charges.

Kurth et al. consider a simple one-dimensional model consisting of a single-level quantum dot coupled to two semi-infinite leads and assume that electronic interactions are only present in the central region. This interacting electronic system is then mapped onto a one-dimensional time-dependent Kohn-Sham system featuring an exchange-correlation potential that has the required derivative discontinuity property [7]. At the initial time, a finite bias voltage is suddenly switched on, and the time evolution of the system is calculated.

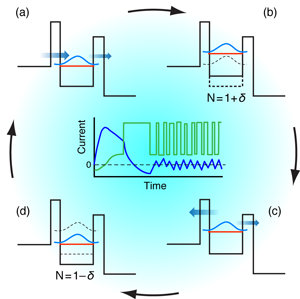
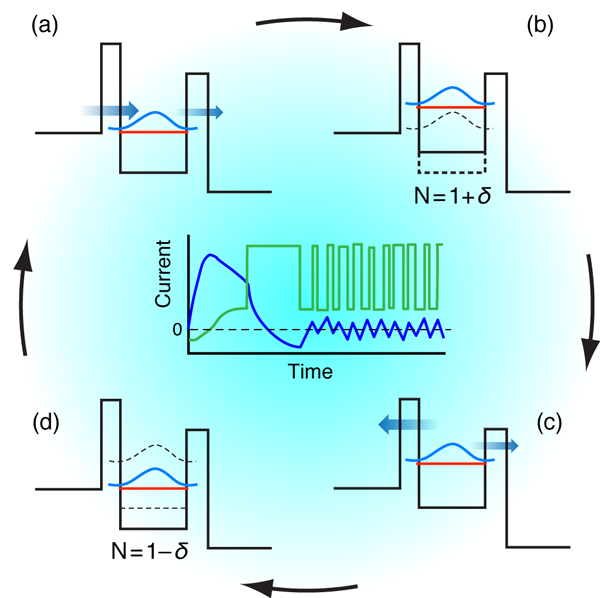
And this is where the surprise occurs: after switching on the bias, the system—unlike what more restricted models predict—does not evolve towards a steady state (Fig. 2)! It turns out that a steady Coulomb blockade state only exists if the voltage is switched on adiabatically; in that case, the Landauer-DFT results are recovered. In all other cases, one observes a transient phase followed by persistent and self-sustained current oscillations, which indicate a periodic charging and discharging of the dot, with an average occupation corresponding to the Coulomb blockade state.

The discontinuity of the exchange-correlation potential is responsible for this, as shown in Fig. 2. Driven by the bias, charge density is continuously accumulating on the dot until it reaches an integer value, at which point the potential jumps up, causing some of the charge to flow back out again, and the process repeats. The resulting current oscillations are more pronounced the faster the bias is initially switched on. Coulomb blockade thus emerges as an intrinsically time-dependent phenomenon, and this behavior cannot be captured with the Landauer-DFT “standard model.”

The real-time time-dependent DFT approach for transport opens up many new research avenues. On the theoretical side, one obvious task is to go beyond simple model systems and simulate transport using more realistic descriptions of nanoscale junctions—say, putting a real molecule or nanocrystal between actual metallic leads. The development and application of exchange-correlation potentials with discontinuities remains a key issue [8]; it will also be of interest to see how the dynamical Coulomb blockade is affected by the presence of dissipation, e.g., as caused by memory-dependent exchange-correlation potentials [9,10].

The potential practical applications span a wide range of systems such as single-electron transistors and other nanoscale logic or memory devices. Whenever these devices are switched rapidly (on timescales shorter than a picosecond), transient and non-steady-state effects such as the ones considered here will become relevant. Thanks to the work by Kurth et al. we now have the theoretical and computational tools to simulate from first principles what these processes will look like.

References

S. Kurth, G. Stefanucci, E. Khosravi, C. Verdozzi, and E. K. U. Gross, Phys. Rev. Lett. 104, 236801 (2010)
M. Di Ventra, Electrical Transport in Nanoscale Systems (Cambridge University Press, Cambridge, 2008)[Amazon][WorldCat]
M. Koentopp, C. Chang, K. Burke, and R. Car, J. Phys. Condens. Matter 20, 083203 (2008)
W. Kohn, Rev. Mod. Phys. 71, 1253 (1999)
C. Toher, A. Filippetti, S. Sanvito, and K. Burke, Phys. Rev. Lett. 95, 146402 (2005)
Time-dependent density functional theory, Lecture Notes in Physics Vol 706, edited by M. A. L. Marques, C. A. Ullrich, F. Nogueira, A. Rubio, K. Burke, and E. K. U. Gross (Springer, Berlin, 2006)[Amazon][WorldCat]
N. A. Lima, M. F. Silva, L. N. Oliveira, and K. Capelle, Phys. Rev. Lett. 90, 146402 (2003)
D. Vieira, K. Capelle, and C. A. Ullrich, Phys. Chem. Chem. Phys. 11, 4647 (2009)
N. Sai, M. Zwolak, G. Vignale, and M. Di Ventra, Phys. Rev. Lett. 94, 186810 (2005)
H. O. Wijewardane and C. A. Ullrich, Phys. Rev. Lett. 95, 086401 (2005)

About the Author

Carsten A. Ullrich is an Associate Professor of Physics at the University of Missouri-Columbia. He obtained his Ph.D. in theoretical physics in 1995 from the University of Würzburg, Germany. His main research interests are the fundamental and practical aspects of time-dependent density-functional theory, with an emphasis on transport, collective excitations, and excitonic effects in bulk and nanostructured semiconductor materials. In 2009 he was recognized as an Outstanding Referee by the American Physical Society.