Split light

Jacek K. Furdyna

Viewpoint

Split light

Department of Physics, University of Notre Dame, Notre Dame, IN 46556, USA

July 6, 2010• Physics 3, 56

A little-known and subtle optical effect in combination with state-of-the-art pulsed laser techniques holds considerable promise as a sensitive way to study physical properties (including spin phenomena) in nanometer scale structures.

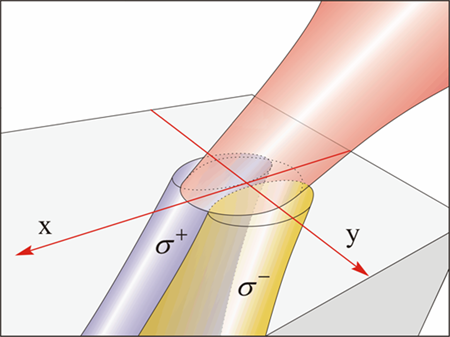
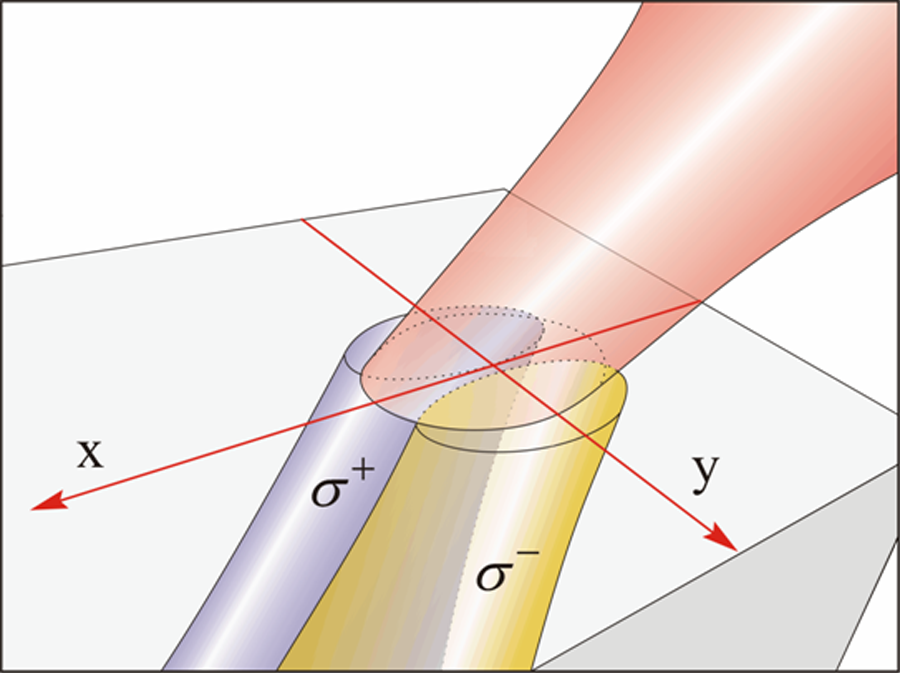
Figure caption — **Figure 1:** Schematic illustration of the spin Hall effect of light (SHEL). When a linearly polarized light beam is incident obliquely on an interface between two media with different indices of refraction, its circularly polarized components with opposite helicities ( $σ^{+}$ and $σ^{-}$ ) are separated spatially in the direction perpendicular to the plane of incidence, as shown. The separation is on the subwavelength scale, but can easily reach values of $200 nm$ or more, and can be tuned by varying the angle of incidence.

The behavior of a light beam obliquely incident on a plane interface can be described rather completely via well-established theory, and one does not expect many surprises or novelty. There is, however, a subtle, and at the same time, fascinating effect that also occurs at oblique incidence, unfamiliar to most physicists. One can show that when light is incident on a plane interface between different media at oblique incidence, a spatial separation of the circularly polarized components of the incident light beam (which we will refer to as $σ^{+}$ and $σ^{-}$ ) occurs, essentially as shown in Fig. 1. The separation is minute—less than a wavelength—but real, and can lead to new insights and new practical uses.

This subtlety, sometimes referred to as the Fedorov-Imbert effect, was predicted theoretically by Fedorov as early as 1955 [1], and was experimentally confirmed by Imbert in 1972 [2]. The theory was extended by Onoda et al. [3] in a formulation which shows that the spatial separation of the $σ^{+}$ and $σ^{-}$ polarizations on oblique incidence stems directly from the conservation of the $z$ component $j_{z}$ of the total angular momentum $j$ of the light beam [4].

Until recently, experimental exploration of this fascinating effect has largely been limited to air-glass interfaces, with an eye on the experimental confirmation of the predicted separation of the two circular polarizations, and on devising various methods whereby the resolution of this tiny separation can be enhanced and measured [5]. In comparison, little attention has been given to what information can be obtained from this effect about the properties of the materials comprising the interface. This, however, is potentially a very important question: the spatial separation of the $σ^{+}$ and $σ^{-}$ polarizations depends on the indices of refraction of the two media, and thus can be exploited for investigating their various constitutive properties. In an article appearing in Physical Review B, Jean-Michel Ménard, Adam Mattacchione, and Henry van Driel from the University of Toronto, Canada, with Christine Hautmann and Markus Betz from the Technical University of Munich, Germany, address precisely this issue in a pioneering way [6].

To proceed, let us first define the geometry we will use to describe the effect. We assume the interface is in the $x$ - $y$ plane, $z$ being the direction of the normal, and we take the wave vector of the oblique light beam to be in the $x$ - $z$ plane (the plane of incidence), as shown in Fig. 1. In discussing oblique incidence it is customary to resolve the incident light into two linearly polarized components, one with the electric vector $E$ in the plane of incidence (the so-called “ $p$ polarization”), and the other with $E$ in the $y$ direction (the “ $s$ polarization”). Any linearly polarized wave can, of course, itself be resolved into two counter-rotating $σ^{+}$ and $σ^{-}$ circular polarizations—clockwise and counterclockwise with respect to the direction of propagation. In this geometry, the $σ^{+}$ and $σ^{-}$ components of a light beam obliquely incident on the interface will be shifted laterally with respect to each other in the $y$ direction, essentially as shown in Fig. 1.

This effect has an analog in condensed matter physics—the so-called spin Hall effect—where electrons or holes propelled by an electric field (say, along $z$ ) separate along the $y$ direction, depending on their spin, even in the absence of a magnetic field [7]. Since the $σ^{+}$ and $σ^{-}$ polarizations represent the intrinsic angular momentum of light—the “spin” of the photons—their spatial separation along $y$ (depicted in Fig. 1 ) can thus be imagined as the optical analog of the spin Hall effect in solids, if we view the gradient of the refractive index at the interface as the analog of the applied electric field; hence the term: “spin Hall effect of light” (SHEL). While both effects have their physical origin in spin-orbit interaction in their respective contexts, one should be careful not to take these similarities too literally, but rather to use the spin Hall effect simply as a convenient analog. In the spirit of this analogy, one can immediately see that in order to observe the effects of the lateral separation $d$ of the $σ^{+}$ and $σ^{-}$ polarizations, a light beam of finite cross section (focused as tightly as possible) is required—just as the spin Hall effect can only be observed in a planar sample with a finite lateral dimension as a result of spins accumulating on boundaries. Expressions for this lateral separation have been a matter of some debate, but it is now well established that $d$ is proportional to the wavelength of the incident light and varies strongly with the angle of incidence $ϕ_{i}$ : it disappears for normal incidence ( $ϕ_{i} = 0$ ), and becomes most pronounced as $ϕ_{i}$ approaches $90$ º. Obviously SHEL also depends on the refractive index, thus implicitly containing information on the materials that comprise the interface.

Ménard et al. apply the study of SHEL to semiconductors and focus on investigating the connection between this subtle optical effect and the material parameters and physical phenomena that determine the index of refraction of the medium on which the light beam is incident. This establishes a link between SHEL and condensed matter physics that is of particular importance: by spatially separating the $σ^{+}$ and $σ^{-}$ polarizations (each of which couples to different spin states of electrons in the medium), SHEL has the potential of probing spatial distributions of electron spin states, and of doing so at the nanometer scale. This is particularly exciting at a time when spin effects in solids are gaining increased interest because of their potential in spintronics, and when different structures involving such spin effects can be fabricated with subnanometer precision. Here one should add that the nanoscale spatial separation of the $σ^{+}$ and $σ^{-}$ polarizations can be “tuned” continuously by varying the angle of incidence, and that the incident light beam can be scanned across the interface using highly precise piezoelectric methods, thus making SHEL a promising tool for mapping spin properties on a scale compatible with the dimensions of nanostructures obtainable by various epitaxial and lithographic methods. While studies of such nanostructures are not the explicit subject of the article, by establishing the relevance of SHEL to several physical phenomena in quintessential semiconductor materials ( $Si$ and $GaAs$ ), the authors have automatically paved the way toward such more complex situations. It should also be noted that by using semiconductors (which typically have large indices of refraction), the authors have observed SHEL separations of the order of $200 nm$ , much larger than those in earlier experiments involving air-glass interfaces.

In a nutshell, the authors use SHEL to study three physical effects occurring in these materials: free carrier absorption (as the simplest example of optical absorption in SHEL), Pauli blocking (as an example of the sensitivity of SHEL to electron spin states in semiconductor bands), and (as an example of nonlinear interactions) two-photon absorption. In the interest of brevity, I will not discuss the physics of each of these processes—this is presented with pedagogical clarity in Ref. [6]. It is important to point out, however, that in their approach, the authors bring about another dimension to their experiments by using ultrafast pump-probe methodology to explore SHEL in these semiconductors. By impinging on the semiconductor, the tightly focused pump beam creates a change in the properties of the medium of interest, e.g., by creating free carriers. The authors refer to the area modified by the pump beam as the “aperture,” which is then probed by the probe beam (obliquely incident, and thus exhibiting SHEL). An important refinement made available by the use of ultrafast spectroscopy is the time-delay capability of the probe, resulting in measurements tailored to the species of interest. For example, in the Pauli blocking experiment the probe beam arrives after the spins of the holes (which are very short-lived) have relaxed, so that the absorption of the $σ^{+}$ and $σ^{-}$ polarizations at their respective positions is sensitive only to spin states of the electrons generated by the pump. Furthermore, by spatially scanning the pump beam (along the $y$ direction in Fig. 1), the authors are able to use a differential absorption procedure, which is highly sensitive to the value of the SHEL separation $d$ , thus providing a reliable measure of this parameter in the medium under investigation [8]. While these additional points are rather in the category of experimental details, they do deserve mention here because, to my knowledge, this is the first time they are used in the context of SHEL, providing important additional extensions in the study of this effect in solids.

The combination of the spin Hall effect of light with the elegant and powerful methods of ultrafast spectroscopy and spatial scanning procedures illustrates the exciting opportunities that this effect offers for investigating solids. Since the two spatially split circular polarizations, $σ^{+}$ and $σ^{-}$ , couple to transitions between electronic levels with different spin, these advances in the use of SHEL are particularly exciting at a time when spin effects in semiconductors are assuming an increasingly important role in contemporary research. For example, one can imagine that with further refinements (including possible use of multiple light beams) SHEL can be used to generate complex electron spin systems that can be “landscaped” in time and space with nanoscale resolution to achieve new functionalities.

References

F. I. Fedorov, Dokl. Akad. Nauk SSSR 105, 465 (1955)
C. Imbert, Phys. Rev. D 5, 787 (1972)
M. Onoda, S. Murakami, and N. Nagaosa, Phys. Rev. Lett. 93, 083901 (2004)
For a discussion of the total angular momentum of light, see M. Padgett, J. Courtial, and L. Allen, Physics Today 57, No. 5, 35 (2004)
O. Hosten and P. Kwiat, Science 319, 787 (2008)
J-M. Ménard, A. E. Mattacchione, H. M. van Driel, C. Hautmann, and M. Betz, Phys. Rev. B 82, 045303 (2010)
Y. K. Kato, R. C. Myers, A. C. Gossard, and D. D. Awschalom, Science 306, 1910 (2004)
The pump beam may or may not exhibit SHEL, but this is not essential for the experiment in hand. In an earlier experiment some of the authors also used an alternate approach, where the pump beam is incident obliquely, thus producing excitation by the $σ^{+}$ and $σ^{-}$ polarizations at spatially separated points of the interface, and scanning is carried out by a normally incident probe beam, also with very interesting results. See J.-M. Ménard, A. E. Mattacchione, M. Betz, and H. M. van Driel, Opt. Lett. 34, 2312 (2009)

About the Author

Jacek K. Furdyna is Marquez Professor of Physics at the University of Notre Dame. He received his Ph.D. in experimental solid-state physics at Northwestern University in 1960, where he subsequently held a postdoctoral appointment in electrical engineering. He then joined the staff of M.I.T.’s Francis Bitter National Magnet Laboratory, where he worked on plasma effects in solids. After four years at M.I.T. he joined the Physics Department at Purdue University, where he continued his studies of solid-state plasmas and in 1969 began research on diluted magnetic semiconductors. In 1987 he joined the Physics Department at the University of Notre Dame as Marquez Professor of Physics. At Notre Dame his work focused on epitaxially grown magnetic semiconductors and their quantum structures. In recognition of his work he was awarded honorary doctorates by Warsaw University and Purdue University, and the Copernicus Medal by the Polish Academy of Sciences. In 2008 he was recognized as an Outstanding Referee by the American Physical Society.