Galaxies weigh in on neutrinos

Julien Lesgourgues

Viewpoint

Galaxies weigh in on neutrinos

CERN, Theory Division, CH-1211 Geneva 23, Switzerland
Institut de Théorie des Phénomènes Physiques, EPFL, CH-1015 Lausanne, Switzerland
LAPTh (CNRS - Université de Savoie), BP 110, F-74941 Annecy-le-Vieux, Cedex, France

July 12, 2010• Physics 3, 57

A comparison between the density in surrounding galaxies today and a few billion years ago provides a new upper bound on neutrino mass.

Figure caption — **Figure 1:** Comparison of density distribution in the Universe with (left) and without (right) massive neutrinos. The maps are based on numerical simulations [8]. The colors account for the density of ordinary (baryonic) matter in one slice of the simulation box [9]. The two simulations started from the same initial conditions, with either $M_{ν} = 0$ (right) or $M_{ν} = 1.9 eV$ (left). In the massive neutrino case, matter is spread over a larger number of structures and there is less density contrast. (The unrealistically large neutrino mass of $1.9 eV$ was chosen so as to make the comparison clear.)

Neutrinos are infamously lightweight particles that are near impossible to detect, let alone place on a scale. Yet our most basic model for understanding the symmetries of matter and particles rests on an accurate measure of the neutrino masses.

Over the past decade, observational cosmology has taken a leading position in providing an upper bound on these masses. Now, in a paper appearing in Physical Review Letters, Shaun Thomas, Filipe Abdalla, and Ofer Lahav at University College London in the UK [1] predict that the total neutrino mass, summed over the three neutrino families, is smaller than $0.28 eV$ —the tightest upper bound yet. Their prediction is based on a new mapping of the distribution of density of surrounding galaxies.

Until recently, neutrinos were described in the standard model of particle physics as massless particles with three “flavor states”: the electron, muon, and tau neutrino. The 1998 discovery at Japan’s Super Kamiokande neutrino observatory that neutrinos oscillate between these flavor states brought the first direct experimental evidence for new physics beyond the standard model and lead to the picture that neutrino particles should be viewed as three “mass states,” each of which is composed of a mixture of the three flavor states in fixed proportions that are parametrized by “mixing angles.” Flavor oscillations depend on these angles, as well as on the differences between the squares of each mass. The details of this model are, however, still uncertain.

In fact, because neutrino particles are so light and difficult to measure, they come saddled with a host of enigmas: Do neutrinos have the same mathematical structure as quarks and electrons (namely, “Dirac fermions”) or a yet unobserved structure in which they would be their own antiparticle (referred to as “Majorana fermions”)? Do their interactions violate charge-parity (CP) symmetry as is the case for quarks? What is the origin of their mass? What role did they play in the early evolution of the Universe that explains the excess of matter over antimatter that we now observe? Addressing these questions through all possible experimental techniques gives us an opportunity to probe new sectors of particle physics.

Over time, experiments have yielded various bounds on neutrino masses. For example, the probability of flavor oscillation for solar or atmospheric neutrinos gives access to two mass square differences, but such results provide a lower bound on only two out of the three masses, and no upper bound on any of them. Currently, the lower bound on the largest neutrino mass is $0.05 eV$ . Tritium beta decay experiments are able to provide an upper bound on the sum over the three neutrino masses, $M_{ν}$ , but it is still on the order of $7 eV$ [2]. Germany’s KATRIN experiment, a next generation tritium beta-decay experiment starting in 2012, could tighten this bound by another order of magnitude.

Cosmological observations provide independent constraints on the neutrino mass scale almost for free. Indeed, the primary goals of space-based and ground-based experiments that map cosmic microwave background (CMB) anisotropies and the large scale structure of the Universe are to understand its global evolution from very early times to today, and to probe the nature of dark matter and dark energy. Without any further efforts, the same experiments return an estimate (or, currently, an upper bound) on $M_{ν}$ .

It may sound paradoxical that the mass of the lightest known particles can be inferred from information on the global Universe evolution. The reason is that neutrinos were produced very abundantly at early times. Today, despite the diluting effects of an expanding universe, we are, on average, immersed in a background of $339$ relic neutrinos per centimeter cube. If all neutrinos had a mass of $0.05 eV$ , they would sustain about one per cent of the total mass of the Universe.

CMB observations provide precise measurements of the evolution and composition of the Universe starting from a time when its temperature was roughly one million kelvin (i.e., a thermal energy of just under $100 eV)$ . In such conditions, neutrinos would be considered ultrarelativistic and the radiative background consisting of (at least) photons and neutrinos would have dominated the density of the Universe. Today, the average temperature is as low as $2.726 K$ , meaning that typical relic particles with a mass greater than $10^{- 4} eV$ are nonrelativistic. Hence neutrinos should be counted in the budget of nonrelativistic matter today, while they would be classified as relativistic matter in the past. Such a “leak” from one category to the other is a rather specific effect of a neutrino having a small, but finite mass. By measuring the time of matter-radiation equality and other parameters, CMB observations can probe this leak and provide a bound on the total mass. For example, current data from the Wilkinson Microwave Anisotropy Probe (WMAP) satellite indicate that $M_{ν} < 1.3 eV$ [3], while the same data combined with other probes of the background cosmological evolution yield $M_{ν} < 0.58 eV$ .

This rather indirect measurement is subject to an issue of parameter degeneracy that limits the bounds on $M_{ν}$ : the effect of one cosmological parameter (in our case, of $M_{ν}$ ) on the CMB can be mimicked to some extent by the variation of other parameters. This will occur if the data is not precise enough, or if one assumes a very general cosmological model with many free parameters.

Cosmological observations could provide robust and accurate bounds only if there were a more direct signature of neutrino masses. By chance, such an effect exists and was already described by theorists in the 1980s [4]. Structures like galaxies and clusters were formed by gravitational collapse, between the time at which the Universe became transparent and today, at a rate governed by the balance between gravity and cosmological expansion. Cosmological expansion increases all distances, weakens gravitational interactions, and slows down the formation of structures. Since massive neutrinos contribute to the total density of the Universe, they tend to increase the expansion rate. However, on small length scales, they do not contribute to gravitational collapse. (Neutrinos have a large velocity dispersion, which prevents them from falling in potential wells below a characteristic distance called the free-streaming length.) On short length scales, neutrinos that have mass tip the balance towards less gravity and more expansion, slowing down the rate at which structures form and making them less abundant than they would be in a Universe with massless neutrinos.

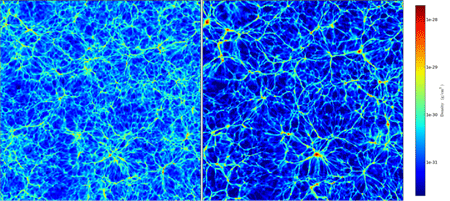
This effect is cumulative over time and is sensitive to very small neutrino masses. For instance, if the total neutrino mass was close to $0.05 eV$ (the minimum allowed value), neutrinos would contribute at most $0.4 %$ of the energy density during structure formation and would only suppress the growth rate of structures by a tiny amount at a given time. But after a few billion years, even this tiny effect on structure formation would reduce the squared variance of density inhomogeneities by as much as $3.5 %$ (see Ref. [5] for a review). The numerical simulations displayed in Fig.1 illustrate this effect.

These arguments mean that a careful study of the formation rate of structures in the recent past of the Universe offers a unique opportunity to measure the absolute neutrino mass scale. The work by Thomas et al. represents an important step forward in this direction. Similar analyses were carried out in the past, but not with such suitable data. Thomas et al. based their estimates on a new three-dimensional map of galaxies that they reconstructed using the Sloan Digital Sky Survey data, taken with the telescope at the Apache Point Observatory in New Mexico, US. The use of so-called “photometric redshift estimates” allowed Thomas et al. to build a map on much larger scales than before, providing an indication of the distribution of structures not only in a recent past but also a few billion years ago when the most remote galaxies in this map emitted the light that we observe today.

The data are particularly appropriate for testing the impact of neutrino masses on the formation rate of structures, both on length scales smaller and larger than the neutrino free-streaming scale. In combination with WMAP and other probes of the background cosmological evolution, the analysis of this new data provides an upper bound of $M_{ν} < 0.28 eV$ at a $95 %$ confidence level—twice smaller than without galaxy data. Moreover, because the galaxy data directly probe the free-streaming effect of neutrinos during structure formation, they are less subject to parameter degeneracies involving the total neutrino mass compared to other cosmological observables.

This new result is an encouraging milestone. Surveys designed to map the distribution of structure over a wider range of length scales and times, such as weak lensing, cluster catalogues, Lyman-alpha forests in quasar spectra, and $21$ - $cm$ emission line surveys, will push this progress along. (see, e.g., Refs. [5,6]). At the same time, numerical predictions of the effect of neutrino masses on the clustering of small-scale structures are making a good deal of headway [7,8]. Within one decade, cosmological observations should be able to detect the absolute neutrino mass scale, even if the heaviest mass is close to $0.05 eV$ . Ultimately, $21$ - $cm$ surveys could reach an exquisite level of precision and be sensitive to the splitting of the total neutrino masses between the three mass states.

These new bounds will always remain complementary with laboratory experiments, since they probe different quantities (namely, the masses, independently of mixing angles or CP phases) with completely independent systematic errors. In this sense, neutrino physics offers a remarkable example of the interplay between observational cosmology and particle physics.

References

S. A. Thomas, F. B. Abdalla, and O. Lahav, Phys. Rev. Lett. 105, 031301 (2010)
C. Kraus et al., Eur. Phys. J. C 40, 447 (2005)
E. Komatsu et al., arXiv:1001.4538
J. R. Bond, G. Efstathiou, and J. Silk, Phys. Rev. Lett. 45, 1980 (1980)
J. Lesgourgues and S. Pastor, Phys. Rep. 429, 307 (2006)
Y. Mao, M. Tegmark, M. McQuinn, M. Zaldarriaga, and O. Zahn, Phys. Rev. D 78, 023529 (2008)
J. Brandbyge and S. Hannestad, JCAP 01, 021 (2010)
S. Agarwal and H. A. Feldman, arXiv:1006.0689
M.Turk, in Proceedings of the 7th Python in Science Conference, Pasadena, CA, 2008, edited by G. Varoquaux, T. Vaught, and J. Millman, pp. 46-50

About the Author

Julien Lesgourgues is an engineer of the Ecole Polytechnique in Paris. He obtained his Ph.D. in 1998 at the University of Tours, France. He is currently a researcher at CERN and the EPFL in Switzerland and CNRS in France. His research is focused on the phenomenology of cosmological models, and more specifically on the observable signatures of dark matter, neutrinos, and cosmological inflation. He is a member of the Planck satellite collaboration.