Towards colossal magnetoelectricity?
Economists tell us that competition is good for growth. To achieve large, useful, and controllable effects in materials, this same mantra also holds: competition is good. It has been known for quite some time that competing interactions on the microscopic scale can lead to colossal macroscopic effects. A very striking example in recent years has been the colossal magnetoresistance (CMR) effect found in doped manganite perovskites. Chemically doping with holes promotes a ferromagnetic metallic ground state via the double exchange interaction—the hopping of charge between spins via an oxygen atom—as long as the core spins of the ions are ferromagnetically aligned. However, at larger dopings, these charges order to form an insulating charge and orbitally ordered state. The competition between these two phases is at a maximum close to the ferromagnetic transition . Just above , the charge ordering leads to a highly insulating state, while just below , the double exchange interaction produces a ferromagnetic metal. The amplifying effect of competition is realized when applying a magnetic field close to , thereby melting the charge ordering and promoting the ferromagnetic state. The end result is a colossal magnetically induced change in resistivity that can reach as high as orders of magnitude [1].
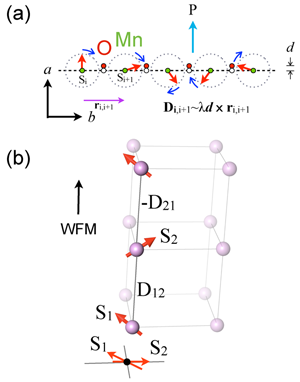
In general, manganites exhibit many interesting effects apart from CMR, the most recent addition to their repertoire being multiferroicity. In multiferroics, ferroelectric polarization is a direct consequence of magnetic order, and both order parameters are coupled. These materials are not doped as their CMR cousins but show a ferroelectric polarization below the onset of a transverse spiral magnetic order [see Fig. 1(a)] that is stabilized when the trivalent lanthanide ion that resides between octahedra is of a sufficiently small size [2]. In this case, antiferromagnetic next-nearest neighbor interactions become stronger and perturb the magnetic order that is otherwise stabilized by nearest neighbor ferromagnetic exchange.
But how does ferroelectricity develop in this situation? A key ingredient here is the spin-orbit interaction in a noncollinear magnet. The transverse spiral order of spins with magnetic propagation vector can be stabilized by the Dzyaloshinskii–Moriya (DM) interaction defined as , where is the Dzyaloshinskii vector and are the individual spins. The direction of the ferroelectric polarization ( ) is then given phenomenologically by the cross product [see Fig. 1 (a)] [2]. What is important here is that the Dzyaloshinskii vector is proportional to the spin orbit coupling [3] and the position of the atom between ions [2]. Since always has the same sign for all pairs of neighboring spins, the DM interaction coherently displaces negatively charged oxygens away from the transverse spiral that is formed by ions [2]. The effect of these atomic displacements is known as the inverse DM interaction and is weak because it arises from relativistic corrections with a strength that is proportional to the spin-orbit coupling.
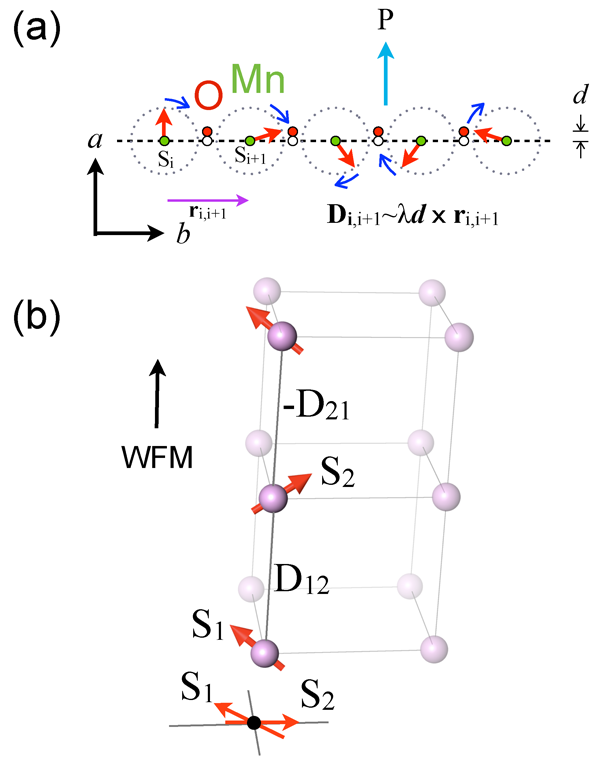
In Physical Review Letters, Young Jai Choi, Chenglin Zhang, Nara Lee, and Sang-Wook Cheong of Rutgers University, US, report how the power of competition can be harnessed in a multiferroic manganite to produce a substantial field-induced magnetoelectric effect similar to CMR [4]. Both competing parameters, oddly enough, arise from DM interactions. The first is the well-known transverse spiral that resides within the plane of the perovskite ( . It propagates along the axis and thus generates a ferroelectric polarization along the axis ( ). The second competing parameter is a weak ferromagnetism (WFM) along the axis that also arises from a small canting of spins in a magnetic field [see Fig. 1(b)]. The ferromagnetism is inherently weak because the canting results in alternating the sign of between pairs of spins. In this situation, WFM can arise with a spontaneous magnetic moment that is proportional to the spin orbit coupling [5]. Despite its small size, this type of WFM is manifested in various first-row transition metal oxides, most notably in the parent compound of cuprate superconductors , where it produces a weak ferromagnetic component in each layer [5].
While the WFM coexists with the transverse spiral, Choi and co-workers find that it occurs at the expense of the ferroelectric polarization when increasing the magnetic field. Why exactly this happens is still not clear; what is clear, however, is that controlling the WFM allows for control of the ferroelectric polarization. Choi and co-workers have indeed demonstrated this idea [4]. They have discovered that while ( is ferroelectric below K with , a weak ferromagnetism is found to be stable between and K, but only for fields above T applied along the axis. The effect of this WFM on the ferroelectricity is substantial, causing an approximately change in the value of over this window of and .
While the modulation of the WFM can be easily achieved by magnetic fields, Choi and co-workers demonstrate that an effect of similar magnitude can also be achieved by applying an electric field. This response is as surprising as it is remarkable because it has been thought that the coupling of magnetism to electric field is much weaker than the coupling between ferroelectricity and magnetic fields in these multiferroics. For example, application of magnetic field on multiferroic or causes the spiral to flop over, producing a flop in the axis of the ferroelectric polarization. However, until now, the same flop has not been realized by utilizing electric fields, despite the fact it is allowed by symmetry. It is possible that the control of the WFM by an electric field is possible due to its estimated small ferromagnetic moment ( per ), while requiring much larger-size fields to flop a transverse spiral of nearly saturated spins.
The work of Choi et al. is reminiscent of CMR, in that the phase lines that separate the WFM from the well-ordered ferroelectric state are all first order and exhibit elements of glassiness. This may indicate that there are physical regions where either WFM or the transverse spiral have short-range ordering, much like that of charge and orbital order in the insulating phase of the CMR manganites. While the size of the magnetoelectric effect described by Choi and co-workers is not exactly of colossal proportions, the analogy to CMR is clear and provokes us to ponder whether the competition between noncollinear and ferromagnetic order can be pushed further to produce a colossal magnetoelectric effect. More generally, however, it suggests that the WFM effect in these multiferroics can become increasingly important, both in terms of producing large magnetoelectric effects as demonstrated by Choi et al., and also possibly in controlling multiferroic domains as was suggested recently for multiferroic ferrites [6]. In any case, the manganites have once again demonstrated that they are indeed full of surprises as well as following the axiom of modern economics that competition is good.
References
- M. Imada, A. Fujimori, and Y. Tokura, Rev. Mod. Phys. 70, 1039 (1998)
- S-W. Cheong and M. Mostovoy, Nature Mater. 6, 13 (2007)
- T. Moriya, Phys. Rev. Lett. 4, 228 (1960)
- Y. J. Choi, C. L. Zhang, N. Lee, and S-W. Cheong, Phys. Rev. Lett. 105, 097201 (2010)
- D. Coffey, T. M. Ric, and F. C. Zhang, Phys Rev B 44, 10112 (1991)
- Y. Tokunaga et al., Nature Mater. 8, 558 (2009)