Major growth in minor hysteresis loops

Chris Leighton

Viewpoint

Major growth in minor hysteresis loops

Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA

September 20, 2010• Physics 3, 79

Hysteresis loop measurements in technologically important magnetic materials have revealed striking deviations from some fundamental and widely accepted concepts in the physics of ferromagnetism.

Figure caption — **Figure 1:** (a) Magnetization hysteresis loops of a $Co (4 Å) / Pt (7 Å)$ multilayer with eight repeats. The heavy line represents the major loop, while the multiple light lines represent the minor loops acquired between $\pm 290 Oe$ . (b) Kerr microscopy images ( $150 \times 150 μ m$ ) of a $Co (4 Å) / Pt (7 Å)$ multilayer with eight repeats, during four successive field cycles. The images were acquired in the negative remnant state.

The concept of hysteresis is fundamental to the physics of ferromagnetism, adding considerably to both the extraordinary richness of the physics displayed, and the diversity in applications of magnetic materials. Simply put, the magnetic state of a ferromagnet depends not only on the external magnetic field experienced at some point in time, but also on the field history, resulting in double-valued magnetization vs field curves referred to as hysteresis loops [1,2]. The parameters characterizing these loops are the most common ones used to describe a ferromagnet’s magnetic response, defining the relevant physical regime, the most suitable models, and possible areas of application [1,2]. These applications vary widely depending on the extent of the hysteresis, from the almost entirely reversible “soft” ferromagnets used in transformer cores to highly hysteretic “hard” permanent magnets used in motors, passing through the precisely engineered materials employed in the recording media of hard disk drives. Although hysteresis loops exhibit complex temperature, time, and frequency dependence, it is widely assumed that macroscopic hysteresis loops are repeatable for a given set of external conditions. This is a remarkable result given the stochastic nature of the magnetization process and the absence of repeatability on a microscopic scale [3–5], deriving only from the sheer scale of the macroscopic averaging.

The simple magnetization hysteresis loops described above are actually more properly referred to as major hysteresis loops, i.e., those for which the starting and ending fields exceed the closure field, where the property of hysteresis vanishes. Minor hysteresis loops, where the maximum applied fields lie below the closure field, are also useful, as they provide additional information on the microscopic details of how the magnetization reverses, in addition to more closely resembling the working field cycle in some applications. They also form the basis for a host of more complex analyses (e.g., Refs. [6–10]), such as the “ $Δ H$ ” [8] and first order reversal curve (FORC) [9,10] techniques, which provide a more detailed picture of the hysteresis mechanisms. Minor loops are thus a major part of the experimentalist’s arsenal when attempting to understand magnetization reversal mechanisms in ferromagnetic materials. However, the uniqueness and repeatability that is so well established for macroscopic major loops is a much more subtle issue for minor hysteresis loops. In fact, measurement of successive minor loops under identical experimental conditions can lead to a “drift” in the shape and size of the minor loop, often referred to as “reptation” (e.g., Refs. [11,12]). Though finite, this and other similar effects [13], have thus far been found to be small, suggesting that they are perhaps best viewed as a “perturbation” to the widely accepted idea of repeatability in macroscopic hysteresis loops.

Given this situation, it is thus a considerable surprise that a paper appearing in Physical Review B, from Andreas Berger, Stephane Mangin, Jeffrey McCord, Olav Hellwig, and Eric Fullerton [14], reports the discovery of strikingly large deviations from this picture. This team, composed of researchers from CIC nanoGUNE (Spain), Nancy-Université (France), Forschungszentrum Dresden-Rossendorf (Germany), Hitachi Global Storage Technologies (US), and the University of California, San Diego, (US) have observed a phenomenon where successive minor loops obtained under identical conditions, rather than being largely repeatable, actually display a massive cumulative expansion, undergoing an increase in hysteresis loss of up to $350 %$ . These results have been reproduced in two materials systems, and, when coupled with a detailed magnetic microscopy study, have enabled the authors to present an explanation for this striking phenomenon in terms of successive accumulation of small nucleation domains, i.e., microscopic areas of reversed magnetization that act as nuclei for the subsequent macroscopic magnetization reversal.

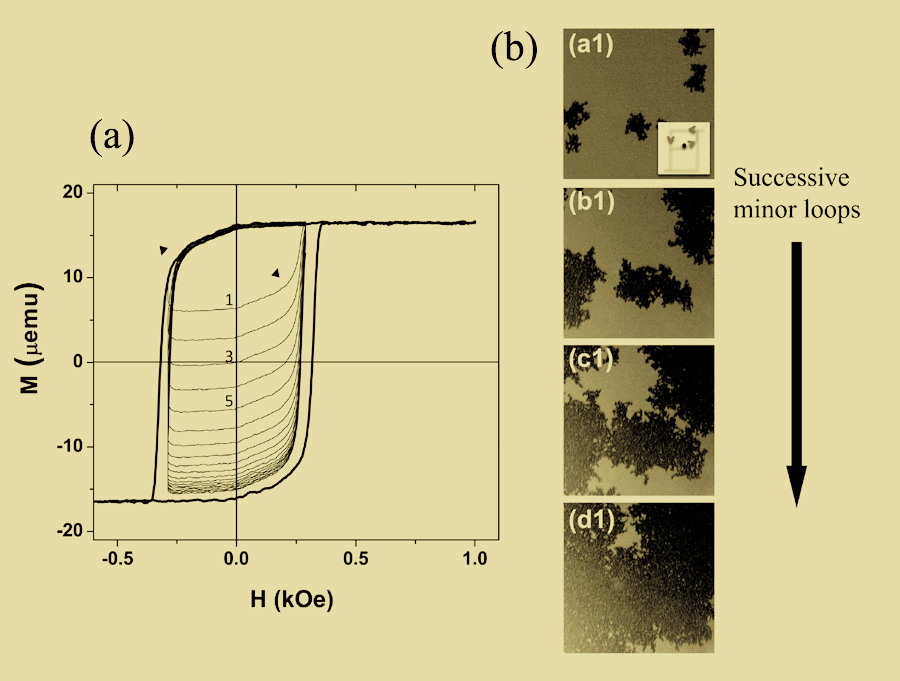
The basic phenomenon is shown in Fig. 1(a), which displays the major hysteresis loop of a $Co/Pt$ thin film multilayer, in addition to a series of successive minor loops obtained by cycling the field between $\pm 290 Oe$ . These multilayered samples are fabricated by sequential physical vapor deposition of multiple ultrathin $Co$ and $Pt$ layers, a process specifically tailored to induce the property of perpendicular magnetic anisotropy [2], which is essential to the operation of modern magnetic recording media. As clearly shown in Fig. 1, successive field cycling results in a dramatic increase in minor loop area, a surprising departure from simple expectations. The authors go on to show not only that this same phenomenon is observed in related $Co/Pd$ multilayers, but also to present detailed information on the dependence on the number of cycles, and the maximum and minimum fields in the minor loop. Two critical observations emerge: (i) this effect disappears for maximum fields that exceed the closure field, showing, somewhat reassuringly, that hysteresis loop repeatability is still a valid concept at sufficiently high field, and (ii) there is a clear correlation between the growth of the minor loops and a small but detectable decrease in the maximum magnetization (i.e., that obtained under the largest positive fields in each cycle). Although it is not visible in Fig. 1(a), this maximum magnetization decreases with successive field cycling (by only $1 %$ or so), in close registry with the expansion in the minor loop area. This subtle effect indicates that the material is not completely saturated at the largest positive fields, providing an important clue to the mechanism of the cumulative minor loop growth.

The key insight into the underlying physical mechanism was provided by magnetic domain imaging, achieved using the magneto-optical Kerr effect [1,2]. Using this technique the authors were able to image the domain structure at various points around the minor loop, repeating this over multiple successive field cycles. The results reveal some striking correlations between the domain patterns, both at different fields within a given minor loop, and between successive minor loops at a given field. The images show not only a memory effect, where the domain pattern recreates that obtained during the previous field cycle, but also, critically, an expansion effect where reverse domains grow laterally with successive field cycling, as illustrated in Fig. 1(b). These data thus demonstrate that the minor loop expansion is driven by successive accumulation of small nucleation domains [15] that apparently assist in subsequent reversals of the magnetization. Interestingly, the resulting domain patterns [e.g., Fig. 1(b), panels (a1)–(d1)] are remarkably similar to what would be expected for a single magnetization reversal, despite the fact that they are collected over multiple successive minor loops.

In addition to demonstrating for the first time that cumulative minor loop growth can be very large (which clearly has important consequences for other analysis methods based on minor loop measurements), and elucidating yet another fascinating phenomenon in the magnetism of perpendicular magnetic anisotropy materials, it is very likely that this work will stimulate additional future research. Although the authors’ domain imaging provides much insight into the reversal mechanism, a physical understanding of the processes underlying the nucleation of such domain structures will require further research. The role of defects in this nucleation process, and the nature of the interaction between the domain walls and the extended defect structure remain open questions [16]. Moreover, it remains to be seen to what extent these results are general. In particular, it is unclear whether effects of a similar magnitude exist in other materials systems, and, if so, what factors contribute to the unusual domain behavior responsible for this effect.

References

B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials (Wiley, Hoboken, 2009)[Amazon][WorldCat]
R. C. O’Handley, Modern Magnetic Materials: Principles and Applications (Wiley, New York, 2000)[Amazon][WorldCat]
D. H. Kim, S. B. Choe, and S. C. Shin, Phys. Rev. Lett. 90, 087203 (2003)
M. S. Pierce et al., Phys. Rev. Lett. 90, 175502 (2003)
M. S. Pierce and et al, Phys. Rev. Lett. 94, 017202 (2005)
I. Tagawa and Y. Nakamura, IEEE Trans. Magn. 27, 4975 (1991)
R.J.M. van de Veerdonk, X. Wu, and D. Weller, IEEE Trans. Magn. 38, 2450 (2002)
A. Berger, Y. H. Xu, B. Lengsfield, Y. Ikeda, and E. E. Fullerton, IEEE Trans. Magn. 41, 3178 (2005); O. Hovorka, Y. Liu, K. A. Dahmen, and A. Berger, Appl. Phys. Lett. 95, 192504 (2009)
C. Pike, A. Roberts, and K. Verosub, J. Appl. Phys. 85, 6660 (1999)
C. R. Pike, Phys. Rev. B. 68, 104424 (2003)
V. G. Lewis, P. I. Mayo, and K. O’Grady, J. Appl. Phys. 73, 6656 (1993)
M. M. El-Hilo, A. L. Al-Momnee, and S. A. Bakar, J. Appl. Phys. 91, 8742 (2002)
J. Ferre and et al, Phys. Rev. B. 55, 15092 (1997)
A. Berger, S. Mangin, J. McCord, O. Hellwig, and E. E. Fullerton, Phys. Rev. B 82, 104423 (2010)
J. E. Davies and et al, Phys. Rev. B. 70, 224434 (2004); Appl. Phys. Lett. 95, 022505 (2010)
For an introduction to this topic, see H. Kronmuller and M. Fahnle, Micromagnetism and the Microstructure of Ferromagnetic Solids (Cambridge University Press, New York, 2003)[Amazon][WorldCat]

About the Author

Chris Leighton is an Associate Professor in the University of Minnesota’s Department of Chemical Engineering and Materials Science. Following a Ph.D. in condensed matter physics at the University of Durham (1998), and a postdoctoral appointment in condensed matter physics at the University of California, San Diego, (1998–2001), he joined the materials science faculty at the University of Minnesota, where he currently holds an endowed chair and is a McKnight Presidential Fellow. His research interests lie primarily in the field of magnetism, currently in complex oxides, highly spin-polarized ferromagnets, spin transport, and magnetic nanostructures and interfaces.