Maxwell’s demon in the quantum world

Juan M. R. Parrondo; Jordan M. Horowitz

Viewpoint

Maxwell’s demon in the quantum world

Juan M. R. Parrondo and Jordan M. Horowitz

Departamento de Física Atómica, Molecular y Nuclear and GISC, Universidad Complutense de Madrid, 28040-Madrid, Spain

February 14, 2011• Physics 4, 13

Extraction of work from a heat bath using the Szilard engine depends crucially on the statistics of indistinguishable particles.

Figure caption — **Figure 1:** (a) The Maxwell demon purportedly violates the second law of thermodynamics by directing hot molecules in a gas to perform work without a heat gradient. The classical Szilard engine, made up of a single molecule coupled to a thermal bath, illustrates how the second law survives because the demon must generate a compensating entropy. (b) Steps in the operation of a quantum Szilard engine. (I) Three molecules are prepared in a closed box with size $L$ . (II) A wall, depicted by a vertical bar, is isothermally inserted at location $l$ . (III) Information on the number of molecules $m$ on the left is acquired by quantum “measurement.” (IV) The wall shifts isothermally to reach its equilibrium location $l_{m}$ . The cycle is complete when the wall is removed isothermally to reach step (I).

Information and thermodynamics are intimately connected. This idea was first illustrated by Maxwell with his celebrated demon: an intelligent being who uses his knowledge about the position and velocity of the molecules in a gas to transfer heat against a temperature gradient without expenditure of work, beating the second law of thermodynamics. The Szilard engine is a stylized version of the demon, where a yes/no measurement of a classical single-particle system allows one to extract a tiny amount of energy, $k T ln 2$ , $k$ being the Boltzmann constant, from a thermal reservoir at temperature $T$ . The engine has been around for almost a century now [1]. Along the way it has furnished insight into the foundations of statistical mechanics, become the canonical model for investigations of feedback-controlled systems, and even spurred the creation of a new field: the thermodynamics of computation.

In a paper appearing in Physical Review Letters [2], Sang Wook Kim at the Pusan National University, Korea, and the University of Tokyo, Japan, along with collaborators from the University of Tokyo analyze a multiparticle quantum version of the Szilard engine, highlighting how the quantum statistics of fermions and bosons can dramatically affect the engine’s performance. The paper helps to clarify the interplay between information and entropy in the quantum world, the thermodynamic consequences of measurement, and the information content of spatially extended multiparticle states.

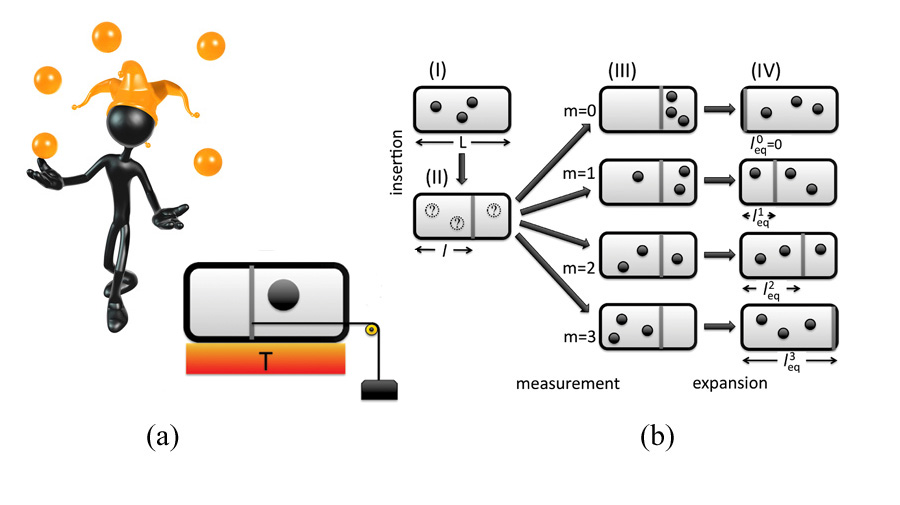
The original Szilard engine consists of a classical particle in a box attached to a thermal reservoir at temperature $T$ . An external agent inserts a wall in the middle of the box, confining the particle in one half. Next, the agent measures in which half of the box the particle is trapped, and then slowly moves the wall to the opposite side of the box, allowing the particle to perform mechanical work. The motion of the wall is an isothermal expansion and the amount of work performed can easily be calculated, $k T ln 2$ . In the classical case, the insertion of the wall can be done, ideally, at zero energy cost. Therefore the whole process results in the extraction of a net amount of energy, $k T ln 2$ , from the thermal bath or a decrease of the entropy by $k ln 2$ . This is precisely the information gathered by the measurement, in the appropriate units (the information in a yes/no measurement is one bit or $ln 2$ nats, a unit of information that uses natural instead of base $2$ logarithms). The second law of thermodynamics demands that this decrease in the entropy must be compensated by an increase in the entropy of the agent operating the engine. This can occur either in the measurement or in the erasure of the information gathered [1]. Sagawa and Ueda have unified both possibilities in a simple and elegant theoretical framework [3].

Despite the age of the problem, the analysis of the Szilard engine continues to benefit from new theoretical and experimental developments. The engine has been studied using a new class of powerful results in nonequilibrium statistical mechanics that characterize the fluctuations in the energetics of arbitrary thermodynamic processes: work and fluctuation theorems. In particular, the extraction of work has been related to the time-reversal asymmetry of the engine’s operation [4,5]. Additionally, the engine has recently been realized in the laboratory—almost one century since Szilard proposed the engine as a gedanken experiment—using a charged Brownian rotor in an electrostatic field controlled by feedback [6].

In their paper, Kim et al. present a general analysis of the isothermal Szilard engine using an arbitrary number of quantum particles. The quantum Szilard engine exhibits intriguing differences with respect to the classical case: the insertion of the wall cannot be done without expending work [7], and the measurement generally involves the collapse of the wave function [1]. Although these subtleties have been analyzed to some extent in previous works, the present article extends these results. Most importantly, by considering two or more noninteracting quantum particles, quantum statistics enters the game, bringing in new effects. For an illustration of the operation of this quantum Szilard engine, see Fig. 1.

Take, for example, the case of two particles: Kim et al. show that the work extracted in one operational cycle is $2 k T f_{0} ln f_{0}$ , where $f_{0}$ is the probability of finding both particles in the same half of the box. For distinguishable particles, $f_{0} = 1 / 2$ , and one recovers the classical result for a single particle. The reason is that although the measurement carries more information ( $2$ bits) than in the one-particle case, two of the possible outcomes (namely, one particle in each half of the box) are not used to extract energy.

More interesting effects occur when both particles are bosons or fermions, especially close to zero temperature where the quantum nature of the particles is more significant. For fermions near zero temperature, the Pauli exclusion principle forces the two fermions to be found in separate halves of the box, thus $f_{0} \approx 0$ and the work extracted is much smaller than in the classical case. On the other hand, at zero temperature, bosons like to clump together. Kim et al. have shown that in this case, $f_{0} = 1 / 3$ , and the work extracted is larger than in the classical case. Consequently, bosons more efficiently extract work from measurement, whereas fermions can be completely inefficient. These differences with respect to the classical case remain even when the thermal energy $k T$ is far above the energy of the ground state.

While the field of quantum information is well developed, we are still a long way from a full understanding of the interplay between information and thermodynamics in quantum systems. Although the paper of Kim et al. does not make explicit use of quantum coherence, it is a first step in this pursuit. Experimental realization of a quantum Szilard engine is still some way off, although potential candidates include trapped cold atoms in the bosonic case and quantum dots from semiconductor heterostructures for the fermionic version.

References

H. S. Leff and A. F. Rex, Maxwell's Demon 2: Entropy, Classical and Quantum Information, Computing (Institute of Physics, Bristol, 2003)[Amazon][WorldCat]
S. W. Kim, T. Sagawa, S. De Liberato, and M. Ueda, Phys. Rev. Lett. 106, 070401 (2011)
T. Sagawa and M. Ueda, Phys. Rev. Lett. 102, 250602 (2009)
R. Kawai, J. M. R. Parrondo, and C. Van den Broeck, Phys. Rev. Lett. 98, 080602 (2007)
J. M. Horowitz and S. Vaikuntanathan, Phys. Rev. E 82, 061120 (2010)
S. Toyabe, T. Sagawa, M. Ueda, E. Muneyuki, and M. Sano, Nature Phys. 6, 988 (2010)
J. Gea-Banacloche and H. S. Leff, Fluct. Noise Lett. 5, C39 (2005)

About the Authors

Juan M.R. Parrondo is a Professor at Universidad Complutense de Madrid, Spain. His research focuses on foundations of statistical mechanics and fluctuations and stochastic processes applied to statistical physics, condensed matter, and biophysics. He obtained his Ph.D. at the Universidad Complutense in 1992.

Jordan M. Horowitz is currently a postdoctoral researcher at Universidad Complutense de Madrid. He received his B.A. in physics and mathematics at Columbia University in New York in 2005 and his Ph.D. in physics from the University of Maryland in 2010. His research interests are the thermodynamics and statistical mechanics of far-from-equilibrium systems and the thermodynamic consequences of feedback and information processing.