A stellar superfluid
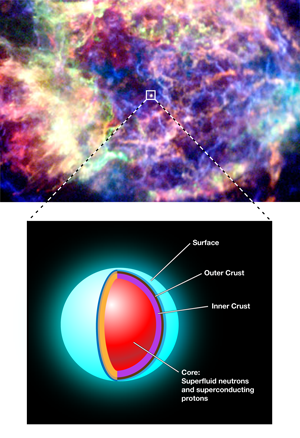
Neutron stars, the compact remnants of certain supernova explosions, are some of the most mysterious objects in the Universe [1]. These peculiar objects have a mass between one and two times that of the Sun, but are packed into a space only across ( times smaller than the Sun’s diameter). The average density of a neutron star can thus exceed a few hundred-thousand billion grams per cubic centimeter—a density several times that found inside the heaviest atomic nuclei. The extreme conditions prevailing in the interior of neutron stars are so far from those encountered in laboratory experiments that the properties of their cores remain largely unknown, and the theoretical description of neutron-star matter is currently one of the most challenging issues of nuclear and particle physics. In a paper appearing in Physical Review Letters, Dany Page at the National Autonomous University of Mexico and colleagues in the US [2] argue there is strong evidence the neutrons in neutron-star cores form a superfluid. This conclusion, which was reached independently by another group headed by Dima Yakovlev from the Ioffe Physical Technical Institute in St Petersburg, Russia [3], is based on recent observations of thermal x-ray emission from the young neutron star lying in the Cassiopeia A supernova remnant (Fig. 1).
Since the fortuitous discovery of radio pulsars by Jocelyn Bell Burnell and Anthony Hewish in 1967, about two thousand neutron stars have been detected. Many more probably exist in our Galaxy. As predicted by William Baade and Fritz Zwicky as early as 1933, neutron stars are born from the catastrophic gravitational collapse of the iron core of massive stars at the end point of their evolution. During the first tens of seconds after the supernova explosion, the newly formed protoneutron star has a radius of about and stays extremely hot, with internal temperatures of the order of a few thousand billion degrees. About one minute later, the protoneutron star becomes transparent to the nearly massless particles called neutrinos that are copiously produced in its interior. This allows the neutrinos to escape easily and carry away energy, so that the protoneutron star cools down rapidly and shrinks into an ordinary neutron star. As the temperature drops below about a billion degrees, the outer layers of the star crystallize into a solid crust. At this point, the core is much colder than the crust because of the cooling power of the escaping neutrinos. After several decades, the interior of the star reaches a uniform temperature of about a hundred million degrees (except for a thin, outer, heat-blanketing envelope). The last cooling stage takes place after about a hundred thousand years, when heat from the interior diffuses to the surface and is dissipated in the form of electromagnetic thermal radiation [4,5].
The metallic surface, which is composed mainly of iron, is generally hindered by a thin atmosphere. A few meters below the surface, matter is so compressed that atomic nuclei, which are arranged in a regular Coulomb lattice, are fully ionized and thus coexist with a quantum gas of electrons. Deeper in the star, nuclei become more and more neutron-rich until neutrons start to drip out of nuclei, forming an underground neutron ocean. Whereas the composition of the outer crust is almost completely determined by experimental atomic masses, the inner crust, where neutrons are unbound, has no equivalent on Earth and thus can only be studied theoretically. The crust dissolves into a uniform liquid of neutrons, protons, and electrons when the density reaches about half that found inside heavy atomic nuclei. At the crust-core, transition nuclei may adopt very unusual shapes, such as rods or slabs. These so-called nuclear “pasta” could account for half of the crustal mass. The composition and the properties of the dense matter in the inner core of a neutron star still remain poorly understood
In particular, it was suggested in 1959, before the actual observations of the first pulsars, that the interior of neutron stars might contain a neutron superfluid—a frictionless liquid with very unusual properties. Superfluidity is one of the most striking macroscopic manifestations of quantum mechanics. Nucleons are fermions, and due to the Pauli exclusion principle, they generally tend to avoid themselves. This individualistic behavior of nucleons, together with the strong repulsive nucleon-nucleon interaction at short distance, provide the necessary pressure to counterbalance the huge gravitational pull in a neutron star, thereby preventing it from collapsing. However, at low enough temperatures, nucleons may form pairs. These pairs are bosons that can behave coherently on a very large scale and the nucleon condensate can flow without any viscosity, analogous to superfluid helium- . (It is interesting to note that, while helium- becomes a superfluid only below a few , superfluidity is sustainable even at a temperature of millions of degrees in a neutron star due to the enormous densities involved.) Even though nuclear pairing has been theoretically studied for several decades [6], the regions of a neutron-star core where this phenomenon could occur are still very uncertain. As shown by the two groups of astrophysicists [2,3], observations of the young cooling neutron star in Cassiopeia A could shed light on this long-standing issue.
Cassiopeia A, which owes its name to its location in the constellation Cassiopeia, is the remnant of a star that exploded years ago at a distance of about light years from us. This central compact object has been only recently identified as a neutron star with a carbon atmosphere and a surface temperature of about two million degrees [7]. The neutron star in Cassiopeia A is not only the youngest known, thermally emitting, isolated neutron star in our Galaxy, but it is also the first neutron star for which the cooling has been directly observed. Ten-year monitoring of this object has revealed that its temperature has dropped by about since its discovery in 1999 by the Chandra x-ray observatory [8]. This cooling rate is significantly faster than that expected from standard neutron-star cooling theories. According to the two teams of scientists who analyzed the Chandra x-ray data to determine the cooling rate, these observations provide strong evidence for superfluidity in neutron-star cores. Indeed, the onset of neutron superfluidity opens a new channel for neutrino emission from the continuous breaking and formation of neutron pairs. This process, which is most effective for temperatures slightly below the critical temperature of the superfluid transition, enhances the cooling of the star during several decades. Based on observations of Cassiopeia A, Dany Page and his collaborators pinpoint the critical temperature of the neutron superfluid to half a billion degrees and argue that the protons in neutron-star cores are superconducting. Yakovlev’s group reached similar conclusions, but their inferred critical temperature for the neutron superfluid is a few hundred million degrees higher because they assumed different microscopic inputs. This rapid cooling is predicted to continue for a few more decades at the same rate. If Page et al.’s interpretation is confirmed by future observations, their results would put stringent constraints on microscopic theories of dense nuclear matter.
References
- P. Haensel, A. Y. Potekhin, and D. G. Yakovlev, Neutron Stars 1: Equation of State and Structure, Astrophysics and Space Science Library 326 (Springer, New York, 2007)[Amazon][WorldCat]
- D. Page, M. Prakash, J. M. Lattimer, and A. W. Steiner, Phys. Rev. Lett. 106, 081101 (2011)
- P. S. Shternin, D. G. Yakovlev, C. O. Heinke, W. C. G. Ho, and D. J. Patnaude, Mon. Not. R. Astron. Soc. (to be published)
- D. G. Yakovlev and C. J. Pethick, Annu. Rev. Astron. Astrophys. 42, 169 (2004)
- D. Page and S. Reddy, Annu. Rev. Nucl. Part. Syst. 56, 327 (2006)
- D. J. Dean and M. Hjorth-Jensen, Rev. Mod. Phys. 75, 607 (2003)
- W. C. G. Ho and C. O. Heinke, Nature 462, 71 (2009)
- C. O. Heinke and W. C. G. Ho, Astrophys. J. Lett. 719, L167 (2010)