A long-distance quantum repeater gets one step closer

Selim M. Shahriar

Viewpoint

A long-distance quantum repeater gets one step closer

Northwestern University, Evanston, IL 60208, USA

July 25, 2011• Physics 4, 58

Researchers demonstrate a robust, high-fidelity, broadband quantum memory that could be used to realize a long-distance quantum repeater for secure communication.

Figure caption — **Figure 1:** A schematic illustration of a process for realizing a long-distance quantum channel by using a quantum repeater. The first step is to create two pairs of entangled photons, using, for example, parametric down conversion. The quantum information in the photons in each pair is transferred to two atomic quantum memories. The two outer quantum memories can be entangled with measurements of Bell states between the two adjacent quantum memories at the center. This doubles the distance over which entanglement is established. Repeating this process—ideally in a nested fashion for higher fidelity—can increase the distance almost arbitrarily.

An example of a quantum memory is a stationary quantum system that can store information encoded in a photon. Such a quantum memory would be an important tool in realizing a quantum repeater—a system that extends the range of a quantum link. A set of quantum repeaters could produce an entanglement between two quantum systems separated by a distance as vast as that between different continents. Such an entanglement, in turn, could form a channel to distribute quantum keys [1] for encrypted communication made secure by fundamental laws of quantum mechanics. In a paper in Physical Review Letters, Klaus Reim and coauthors [2] at the Clarendon Laboratory in Oxford, UK, present a significant step forward in the development of a workable long-distance quantum repeater.

A promising candidate for a quantum memory is a hyperfine transition in a single alkali atom. Such a transition, corresponding to flipping the net angular momentum of the atom while its nuclear and electronic spins remain coupled to each other, can be realized efficiently using an optically detuned Raman transition, where two metastable hyperfine levels are coupled off resonantly to an intermediate excited state. However, it is difficult to make a workable quantum memory based on a single atom. First, the atom has to be held in a dipole force trap—a highly off-resonant and focused beam—loaded from a magneto-optic trap, under a very high vacuum. Second, the vacuum Rabi frequency—the rate at which a two-level atom oscillates when excited by a single photon—for a single atom is very weak, and to capture the quantum information encoded in a photon it has to be coupled to a microscopic cavity made with highly reflective mirrors before it interacts with the atom.

In a recent paper, Duan et al. show [3] a way around this problem by exploiting collective excitations. In their approach, a large number ( $N$ ) of atoms store the quantum information. In the ground state of the collective system, all the atoms are in one of the hyperfine states. The excited state of the collective system is a symmetric superposition of $N$ states, each of which has only one of the atoms in the second hyperfine state [4]. Such a transition has the important property that the vacuum Rabi frequency is enhanced by $\sqrt{N}$ . In a vapor cell operating at room temperature, the value of $N$ can be about $10$ trillion for a volume of one cubic centimeter. The resulting enhancement is so large that even a free-space single photon can be efficiently captured.

Several groups have demonstrated efficient quantum memories using such a collective excitation mediated by optically detuned Raman transitions, in a vapor cell as well as in cold atoms captured by a magneto-optical trap [5,6]. This approach has also been used to generate entanglement between ensembles [7]. The performance of a quantum memory based on cold atoms has been shown to be far superior to that of one based on a vapor cell, in terms of both fidelity and storage time [6,7]. A key deficiency of the conventional approach for a vapor-cell-based collective quantum memory is that the noise floor, caused primarily by collision-induced fluorescence, is unacceptably high for quantum information applications [8].

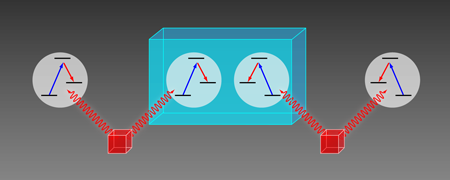
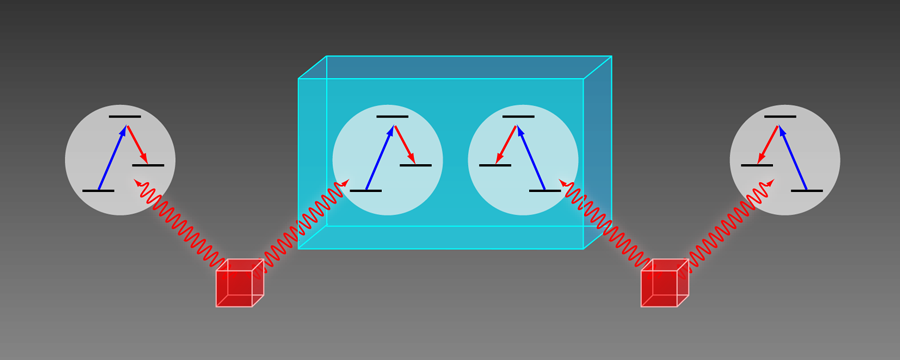
The cold-atom-based quantum memory is, in principle, good enough to realize a quantum repeater that creates a long-distance quantum channel. However, practical problems still prevent us from reaching this goal and it is instructive to consider the process for creating such a channel, as illustrated schematically in Fig. 1. Briefly, the process starts with the creation of two pairs of entangled photons. The quantum information in the photons in each pair is transferred to two atomic quantum memories. By measuring the Bell states [9]—an orthogonal set of entangled states between two quantum systems—between two adjacent quantum memories at the center, the two outer quantum memories can be entangled, thus doubling the distance over which entanglement is established. Repeating this process can almost arbitrarily increase the distance. The measurement of Bell states requires quantum coupling between the quantum memories. Recent theoretical works have shown how such measurements can be performed using collective excitations [10].

For creating a quantum link that works over transcontinental distances, quantum repeaters would have to be placed in remote locations. Quantum memories based on cold atoms would be too fragile, and prohibitively expensive to maintain and operate. Moreover, the best sources of entangled photons to date are parametric down converters—systems that convert a high-energy photon into two photons with lower energies—that produce photons with rather broad spectral width [11]. Since the effective bandwidth of the optically detuned Raman transition employed by such a quantum memory is much narrower, the probability of capturing the quantum information is very small. Narrowband sources of entangled photons are being developed; however, the brightness of such a source is likely to remain very low in the foreseeable future.

In their Letter, Reim and coauthors go a long way towards circumventing these problems. First, their work makes use of room-temperature atomic vapor, a system that is very robust and easy to maintain and operate even in remote locations. Atomic clocks based on vapor cells have been deployed in many harsh environments, including space platforms, and require virtually no maintenance. Second—and this is the key feature—the work makes use of very high optical detuning in the Raman process. The price one pays is that the writing pulse needs to be very intense. Third, the work makes use of very short pulses that satisfy the bandwidth requirement of entangled photon pairs produced by parametric down converters.

The very high optical detuning implies that the degree of excitation to the intermediate level is negligible. Thus the noise due to fluorescence induced by collisions is strongly suppressed. For example, the reported unconditional noise floor is $\sim 0.25$ photons per stored photon, a level that is acceptable for quantum key distribution applications. Furthermore, it is expected that simple refinements of the experiment, such as robust suppression of magnetic fields, would lower the noise floor even further.

Compared to a quantum memory based on cold atoms, the memory storage time is still quite small, only about $4$ microseconds. However, since the stored pulses are very short—about $300$ picoseconds in duration—this storage time is quite long when one considers the more relevant parameter: the product of the storage time and the bandwidth. In this case, the value of this product is about $2500$ , far greater than what has been achieved in other quantum memory systems, including those based on cold atoms.

To summarize, the work reported by Reim et al., employing very highly detuned Raman transitions for a collective quantum memory based on a robust room-temperature vapor cell for storing photons with very short temporal spans, represents a major stride in the development of a practical quantum memory. It brings us a step closer to realizing a transcontinental quantum key distribution system using quantum repeaters, for encrypted communication secured by fundamental laws of quantum mechanics. Much work remains to be done, but the quantum information community would be justifiably excited about this development.

References

A. Ekert, Phys. Rev. Lett. 67, 661 (1991)
K. F. Reim, P. Michelberger, K. C. Lee, J. Nunn, N. K. Langford, and I. A. Walmsley, Phys. Rev. Lett. 107, 053603 (2011)
L. M. Duan, M. D. Lukin, J. I. Cirac, and P. Zoller, Nature (London) 414, 413 (2001)
R. H. Dicke, Phys. Rev. 93, 99 (1954)
B. Julsgaard et al., Nature (London) 432, 482 (2004)
Y. Chen et al., Nature Phys. 4, 103 (2008)
K. S. Choi, H. Deng, J. Laurat, and H. J. Kimble, Nature (London) 452, 67 (2008)
M. T. L. Hsu et al., Phys. Rev. Lett. 97, 183601 (2006)
S. Lloyd, M. S. Shahriar, J. H. Shapiro, and P. R. Hemmer, Phys. Rev. Lett. 87, 16 (2001)
M. S. Shahriar, G. S. Pati, and K. Salit, Phys. Rev. A 75, 022323 (2007)
O. Cohen et al., Phys. Rev. Lett. 102, 123603 (2009)

About the Author

Dr. Selim Shahriar is a Professor in the Department of Electrical Engineering and Computer Science, and in the Department of Physics and Astronomy, at Northwestern University. He is also the Director of the division of solid state and photonics within EECS. He is a member of the Center for Photonic Communication and Computing, and the Center for Interdisciplinary Research and Exploration in Astrophysics. Dr. Shahriar received his Ph.D. from MIT in 1992. His research interests include applications of slow and fast light, quantum computing with trapped atoms, gravitational wave detection, tests of general relativity, holographic and polarimetric image processing, nanophotonics, atomic clocks, atom interferometry, and nanolithography using Bose condensates. He is a member of the LIGO Scientific Collaboration and a Fellow of SPIE and OSA. Group URL: http://lapt.eecs.northwestern.edu/