Supercurrents Get Lean

Chih-Kang Shih; Gregory A. Fiete

Viewpoint

Supercurrents Get Lean

Chih-Kang Shih and Gregory A. Fiete

Department of Physics, The University of Texas at Austin, Austin, TX 78712, USA

November 7, 2011• Physics 4, 92

Electron transport measurements on thin films reveal whether two-dimensional metals support macroscopic supercurrents.

Figure caption — **Figure 1:** In two-dimensional materials like thin films, the formation of Cooper pairs and long-range coherence between the pairs may not occur at the same temperature. This may explain why the $T_{c}$ of a film determined from transport and scanning tunneling spectroscopy (STS) measurements is different.

For a material to transition into a superconducting state, two things have to happen: the electrons must form Cooper pairs (the carriers of superconducting current) and the pairs have to condense into a single phase. In low-dimensional materials, quantum fluctuations may disrupt the superconducting phase even when the Cooper pairs are able to form, leading to the question: How thin can a material be and still superconduct? Advances in synthesizing high-quality, ultrathin metal films have provided unprecedented opportunities to address this question. Experimental evidence suggests that superconductivity persists with a similar transition temperature, $T_{c}$ , even in films that are only $1$ – $2$ atomic layers thick [1,2]; however, these experiments have been based primarily on scanning tunneling spectroscopy, which detects the Cooper pairs, but not the existence of a macroscopic supercurrent. Whether an atomically thin film would also support supercurrents has therefore remained an open question. Now, in a paper appearing in Physical Review Letters, Takashi Uchihashi and co-workers at the National Institute for Materials Science in Tsukuba, Japan, provide a definite answer to this question by showing that robust supercurrents flow over macroscopic distances in an atomically thin metal film of indium [3]. Their work is likely to push theorists and experimentalists to revisit the current understanding of low-dimensional superconductivity.

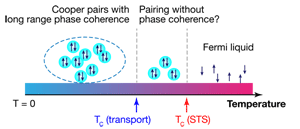
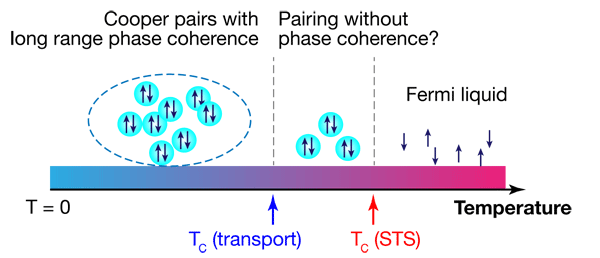
In the conventional picture of superconductivity in a thin film, the state is fragile because phase fluctuations disrupt the long-range phase coherence between Cooper pairs [4]. This picture has been supported by experiments on ultrathin high- $T_{c}$ superconductors [5]. Although early work on thin films of lead, a material that exhibits conventional superconductivity, suggested superconductivity was similarly suppressed at around $20$ atomic layers or thinner [6], subsequent experiments discovered superconductivity in these thin films was actually far more robust [7–9]. In particular, even in a two-atom-thick lead film grown on a silicon surface, superconductivity remains strong with a transition temperature of around $4.8 K$ —only a few degrees less than the value found in bulk sample of lead [1]. In 2010, scientists at Tsinghua University in China discovered the existence of surface superconductivity in a single layer of indium atoms adsorbed on silicon [2]. In particular, this film of indium, called the $(\sqrt{7} \times \sqrt{3})$ reconstructed phase because the positions of the indium atoms undulate with a periodicity slightly larger than that of the underlying silicon lattice, has a $T_{c}$ of $3.14 K$ , which is nearly as high as that of bulk indium ( $T_{c} = 3.6 K$ ).

The work reported in Refs. [1,2] used scanning tunneling microscopy to establish the robustness of 2D superconductivity, at least in terms of Cooper-pair formation, in films that are only one to two atomic layers. In contrast, measurements of the bulk resistance or magnetization of the films, both of which should show a pronounced drop at the transition temperature, are needed to probe the macroscopic superconducting phase. These measurements have been performed on thin films of lead that were capped with a protective layer of another material [6,8]. A group at the University of Tennessee [8], for example, showed that below $9$ monolayers of lead, the $T_{c}$ they determined from magnetization measurements was less than that determined using STM. The thinner the film is, the greater the discrepancy in the $T_{c}$ determined by the two types of measurements.

The fact that different methods have yielded different values of $T_{c}$ for ultrathin films raises a fundamental question: Are the local measurements of the superconducting energy gap (using STM) and the macroscopic measurements revealing different information? If this difference is real, then it would imply that there is a range of temperatures where Cooper-pair formation is robust, while the long-range phase coherence is not (Fig. 1). This phenomenon appears to be unique to superconductivity in two dimensions, since pair formation and coherence go hand in hand for superconductivity in 3D. However, since the macroscopic measurements were performed on thin films with a thin capping layer, the possibility that the difference occurs because of the capping can’t be ruled out. Unless transport is also measured in situ on the same film, one cannot unambiguously answer this fundamental question.

After creating pristine, “atomically thin” superconducting surfaces of the ( $\sqrt{7} \times \sqrt{3}$ ) phase of indium on silicon in ultrahigh vacuum, Uchihashi et al. make use of a stencil mask and ion sputtering to fabricate a device suitable for transport measurement in situ (i.e., under the same ultrahigh vacuum conditions in which they grew the films). Their observation of robust supercurrents flowing over a macroscopic distance with a $T_{c}$ of $2.8 K$ , close to the $3.14 K$ value reported with STM, makes a definitive statement that long-range phase coherence exists even in this extreme 2D geometry.

In bulk superconductors, the $T_{c}$ determined from measuring the tunneling gap with STM and resistivity generally agree, so the small discrepancy in the transition temperature ( $2.8 K$ vs $3.14 K$ ) might suggest the existence of a narrow temperature window where Cooper-pair formation occurs without long-range phase coherence (Fig. 1). Nevertheless, the possibility of fluctuations in sample preparation or even temperature calibration in different labs can all contribute to this small reported discrepancy. The most unambiguous experiment would require carrying out the transport and the tunneling gap measurements on the same surface.

In their paper, Uchihashi et al. [3] have also investigated the temperature dependence of the critical current, from which they conclude that the atomic steps on the surface act as strongly coupled Josephson junctions. When the indium films are at high enough temperature to behave as normal metals, they have a surface sheet resistance of $410 ohm$ in the normal state. This is an order of magnitude smaller than the critical sheet resistance at which a superconductor becomes an insulator [10]. Increasing the miscut of the silicon surface (that is, cutting the surface at an angle to a well-defined crystallographic direction) increases the density of surface steps. This in turn increases the sheet resistance, so, in principle, it should be possible to control the surface sheet resistance to determine if the superconductor—insulator transition can be observed.

Electronically, the ( $\sqrt{7} \times \sqrt{3}$ ) indium reconstructed surface may not be an “ideal” free standing film. Silicon atoms participate in the formation of the indium surface structure, indicating indium and silicon interact on some level. It will be very interesting to see if one can perform similar measurements on ultrathin lead films, which are electronically more like free-standing films.

Uchihashi et al. [3] have demonstrated the first compelling evidence that the long-range phase coherence of Cooper pairs remains very robust even in such an atomically thin system. Performing these measurements on the mesoscopic scale—for example, at a length scale of the order of the step size, or where one can control the distribution of discrete defects—would be a powerful next step. By combining the ability to control the formation of pristine ultrathin superconducting films at the atomic scale with the ability to probe superconducting properties in situ (using STM or/and transport), researchers are now equipped with tools needed to explore a totally new regime in low-dimensional superconductivity.

References

S. Qin, J. Kim, Q. Niu, and C.-K. Shih, Science 324, 1314 (2009)
T. Zhang et al., Nature Phys. 6, 104 (2010)
T. Uchihashi, P. Mishra, M. Aono, and T. Nakayama, Phys. Rev. Lett. 107, 207001 (2011)
M. Hermele, G. Refael, M. P. A. Fisher, and P. M. Goldbart, Nature Phys. 1, 117 (2004)
I. Hetel, T. R. Lemberger, and M. Randeria, Nature Phys. 3, 707 (2007)
Y. Guo et al., Science 306, 1915 (2004)
D. Eom, S. Qin, M.-Y. Chou, and C. K. Shih, Phys. Rev. Lett. 96, 027005 (2006)
M. M. Özer, J. R. Thompson, and H. H. Weitering, Nature Phys. 2, 173 (2006)
T. Nishio et al., Phys. Rev. Lett. 101, 167001 (2008)
A. M. Goldman and N. Markovic, Phys. Today 51, No. 11, 39 (1998)

About the Authors

Chih-Kang Shih is a Professor of Physics in the Condensed Matter Physics Department at the University of Texas. He received his Ph.D. in 1988 at Stanford University. He was a postdoctoral researcher at IBM Watson Research Center until 1990 when he joined the University of Texas as an Assistant Professor. He became a full Professor in 2000. His research interests include ultrathin film growth, quantum phenomena in low-dimensional electronic systems, optical spectroscopy, and electronic properties of semiconductor nanostructures.

Gregory Fiete received his Ph.D. in physics from Harvard University in 2003. After a postdoc at the Kavli Institute for Theoretical Physics at the University of California, Santa Barbara, he moved to Caltech as a Lee A. DuBridge Prize Fellow in Theoretical Physics. He is currently an Assistant Professor at the University of Texas at Austin. His research interests span a wide range of areas within condensed-matter physics, with recent topics including topological insulators, frustrated magnetism, strongly correlated one-dimensional systems, and the fractional quantum Hall effect.